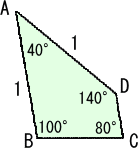
A＝40°、B＝100°、C＝80°、D＝140°、AB＝AD＝1　であるような四角形ABCDの面
積を求めてください。

　　　　　


（コメント）　面白そうな問題だったので、解いてみました。

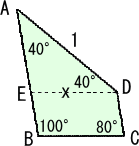辺ＡＢ上に、ＥＤとＢＣが平行となるように点Ｅをとる。このとき、 　△ＡＥＤは２等辺三角形で、ＥＤ=ｘ とおくと、　ｘ=1/（2ｃｏｓ40°） 　　よって、四角形ＡＢＣＤの面積は、 　ｓｉｎ40°/（4ｃｏｓ40°）+（1−1/（2ｃｏｓ40°））ｓｉｎ80°/（2ｃｏｓ40°） 　　　=ｓｉｎ40°-ｓｉｎ40°/（4ｃｏｓ40°） 　　　=（2ｓｉｎ80°-ｓｉｎ40°）/（4ｃｏｓ40°）

　ところで、　θ=40°とおくと、　3θ=120°から、　2θ=120°-θ　なので、

　ｓｉｎ80°=（/2）ｃｏｓ40°-（-1/2）ｓｉｎ40°より、　2ｓｉｎ80°-ｓｉｎ40°=ｃｏｓ40°

　以上から、四角形ＡＢＣＤの面積は、ｃｏｓ40°/（4ｃｏｓ40°）=/4


（別解）　ＢＤ²＝1+1-2ｃｏｓ40°=2(1-ｃｏｓ40°)=4ｓｉｎ²20°より、ＢＤ=2ｓｉｎ20°

　△ＡＢＤは２等辺三角形なので、∠ＤＢＣ=30°より、ＢＤｓｉｎ30°=ｓｉｎ20°

　ＢＣ=ＥＤ=1/（2ｃｏｓ40°）なので、四角形ＡＢＣＤの面積は、

　ｓｉｎ40°/2+ｓｉｎ20°/（4ｃｏｓ40°）
=(ｓｉｎ80°+ｓｉｎ20°)/（4ｃｏｓ40°）
=2ｓｉｎ50°ｃｏｓ30°/（4ｃｏｓ40°）
=ｃｏｓ40°/（4ｃｏｓ40°）
=/4


（コメント）　特殊な図形で何かあるかな？と思いつつ面積を求めたところ、割と綺麗な結果
　　　　　　に驚いています。初等幾何的な解法はあるのでしょうか？


　らすかるさんからのコメントです。（平成２８年５月４日付け）

　上図を見ていたら、初等幾何学的な解答を思い付きました。

（別解）　∠PAB=20°となるようにCBの延長上に点Pをとる。このとき、

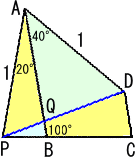△APBは、AP=AB=1、頂角20°底角80°の二等辺三角形、△APD は一辺の長さが1の正三角形となる。さらに、△PCD≡△APB　なので、 　　　　△APQの面積＝四角形BCDQ 　　従って、四角形ABCDの面積＝正三角形APDの面積＝/4

（コメント）　なるほど！上手く正三角形が隠れていたのですね。らすかるさんに感謝します。


　Ｓ（Ｈ）さんの紹介でＨＮ「壊れた扉」さんの別解もいただきました。（平成２８年５月４日付け）

（別解）　△ＡＢＤは底角７０°の二等辺三角形なので、∠ＤＢＣ＝３０°より、∠ＢＤＣ＝７０°

　ここで、ＤＡ上にＤＥ＝ＤＣとなる点Ｅを取ると、△ＤＢＥ≡△ＤＢＣ　で、∠ＥＢＣ＝６０°より、

∠ＥＢＡ＝４０°すなわち、∠ＥＡＢ＝∠ＥＢＡ　より、△ＥＡＢは二等辺三角形。

　今、ＡＢを底辺として頂角が点Ｄ側にある正三角形ＦＡＢを描き、ＤＦ、ＥＦを結ぶと、

　　ＡＢ＝ＡＦ　、ＡＢ＝ＡＤ　より、　ＡＤ＝ＡＦ　なので、△ＡＤＦは二等辺三角形

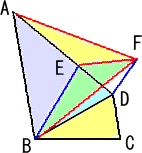ここで、∠ＤＡＦ＝２０°より、∠ＡＤＦ＝８０° 　　　また、∠ＢＥＤ＝８０°より、∠ＡＤＦ＝∠ＢＥＤ　なので、 　　ＢＥとＤＦは平行である。 　　ところで、△ＦＡＢが正三角形で、△ＥＡＢが二等辺三角形より、 　　△ＦＥＡ≡△ＦＥＢ・・・(*)　また、△ＤＥＢ≡△ＤＣＢ・・・(**)　で、 　　等積変形より、　△ＦＥＢ＝△ＤＥＢ・・・(***)

　(*)、(**)、(***)より、　△ＦＥＡ＝△ＦＥＢ＝△ＤＥＢ≡△ＤＣＢ

よって、四角形ＡＢＣＤ＝△ＥＡＢ＋△ＤＥＢ＋△ＤＣＢ
　　　　　　　　　　　　　＝△ＥＡＢ＋△ＦＥＡ＋△ＦＥＢ＝正三角形ＦＡＢ

　以上から、正三角形ＦＡＢの面積を求めれば良いので、面積は、/4


（コメント）　図が若干込み入っていますが、正三角形を作るという方針が貫かれていますね！
　　　　　　Ｓ（Ｈ）さん、壊れた扉さんに感謝します。


　なつさんからのコメントです。（平成２８年５月４日付け）

　遅くなりました。なつです。お返事ありがとうございます。HPは興味深い内容が多く、よく参
考にさせてもらっています。これからの更新も楽しみにしております^^

　図形問題についてですが、/4で正解です。私の意図していた解法をらすかるさんがす
でに投稿しておられますので、私からいうことは何もございません。お見事です。


　DD++さんからのコメントです。（平成２８年５月４日付け）

　sin40° - sin40°/4cos40° = /4　つまり、　4sin40° - tan40° = 　というのを見
て不思議に思ったので調べてみると、以下のような計算が成り立つことがわかりました。

　　4sin20° + tan20° = 　、4sin40° - tan40° =

　　4sin80° - tan80° = -　、4sin100° + tan100° = -

　　4sin140° + tan140° = 　、4sin160° - tan160° = 　　（以下略）

　なんでこんなことが起きるのか不思議に思ったのですが、どうも

　　　tan3θ - tanθ = 2sinθ/cos3θ

なる恒等式が成立するようです。

　よって、3倍すると 60° 絡みになる角度の場合に 4sinθ ±  tanθ のどちらかが ±
のどちらかになります。

　今回の四角形の面積を求める問題は、辺DC上に点Fを菱形ABFDができるように取って
ある状態で、菱形ABFD（sin40°）から三角形BFC（tan40°/4）を切り落とす形で問題を作っ
たのではないかと思います。

　つまり、同じようにしてこんな類似問題を作ることができます。

　AB=AD=1、A=160°、B=40°、C=140°、D=20°であるような四角形ABCDの面積を求め
よ。

　さて初等的に解けるでしょうか？


　らすかるさんからのコメントです。（平成２８年５月５日付け）

　前問と全く同じ方法で解けますね。

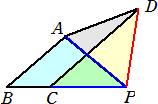BCの延長上に、∠APC=40°となるようにPをとれば、 　△APDは正三角形、△ABP≡△PDCなので、 　　四角形ABCDの面積=△APDの面積=/4

　ＧＡＩ さんからのコメントです。（平成２８年５月５日付け）

　DD++さんに習ってこの図形を解いてみました。成り立つことになる三角関数での関係式を
調べたところ、

cos10°-sin20°=sin40°、cos20°-sin10°=sin50°、cos20°+sin10°=1+tan10°sin40°

が起こることになりそうです。何とか

　　cos10°+sin20°=(1+tan10°sin40°)/tan40°

の関係で繋がれることを見つけました。


　らすかるさんからのコメントです。（平成２８年５月５日付け）

cos10°-sin20°=sin40°、cos20°-sin10°=cos40°、cos20°+sin10°=sin40°

cos10°+sin20°=cos40°

とも表せますね。


（コメント）　私の何とはなしに「3θ=120°」と置いた計算が新たな数式の発見に繋がったよ
　　　　　うで、とても嬉しく思います。DD++さん、ＧＡＩ さん、らすかるさんに感謝します。


（追記）　高校２年生のｋ．ｔ．さんからメールで次のような問題をいただいた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２８年５月２１日付け）

　ｔａｎ（３π/１１）＋４ｓｉｎ（２π/１１）＝　が成り立つことを示せ。

　上記と同じ匂いのする問題であり、ｋ．ｔ．さんからは、「この手の問題は、初等幾何では証
明できませんか？」とのことなので、少し考えてみることにした。

　まずは、代数的な解法から考えてみよう。

（解）　ｘ＝ｅ＾（２πｉ/１１）とおくと、ド・モアブルの定理から　ｘ¹¹＝１　である。

　まず、　ｘ−１/ｘ＝ｅ＾（２πｉ/１１）−ｅ＾（−２πｉ/１１）＝２ｉ・ｓｉｎ（２π/１１）　である。

　　１/ｘ＝ｘ¹⁰　なので、　ｘ−ｘ¹⁰＝２ｉ・ｓｉｎ（２π/１１）

　すなわち、　ｉ・４ｓｉｎ（２π/１１）＝２（ｘ−ｘ¹⁰）

　また、　ｔａｎ（３π/１１）＝ｓｉｎ（３π/１１）/ｃｏｓ（３π/１１）
　　　　　　　　　　　　　　＝２ｓｉｎ²（３π/１１）/２ｓｉｎ（３π/１１）ｃｏｓ（３π/１１）
　　　　　　　　　　　　　　＝（１−ｃｏｓ（６π/１１））/ｓｉｎ（６π/１１）

において、　１−ｃｏｓ（６π/１１）＝１−（ｘ³＋ｘ^-3）/２＝（２ｘ³−ｘ⁶−１）/（２ｘ³）

　　　　　　　ｓｉｎ（６π/１１）＝（ｘ³−ｘ^-3）/（２ｉ）＝（ｘ⁶−１）/（２ｉｘ³）

なので、

　ｉ・ｔａｎ（３π/１１）＝（ｘ⁶−２ｘ³＋１）/（ｘ⁶−１）＝（ｘ³−１）²/（ｘ⁶−１）＝（ｘ³−１）/（ｘ³＋１）

ここで、（ｘ³−１）/（ｘ³＋１）＝（ｘ³−ｘ³³）/（１＋ｘ³）　を実際に割り算して商を求めると、

　（ｘ³−１）/（ｘ³＋１）＝ｘ³−ｘ⁶＋ｘ⁹−ｘ¹²＋ｘ¹⁵−ｘ¹⁸＋ｘ²¹−ｘ²⁴＋ｘ²⁷−ｘ³⁰

　ｘ¹¹＝１　なので、

　（ｘ³−１）/（ｘ³＋１）＝ｘ³−ｘ⁶＋ｘ⁹−ｘ＋ｘ⁴−ｘ⁷＋ｘ¹⁰−ｘ²＋ｘ⁵−ｘ⁸
　　　　　　　　　　　　＝−ｘ−ｘ²＋ｘ³＋ｘ⁴＋ｘ⁵−ｘ⁶−ｘ⁷−ｘ⁸＋ｘ⁹＋ｘ¹⁰

　以上から、

　ｉ・ｔａｎ（３π/１１）＋ｉ・４ｓｉｎ（２π/１１）
＝−ｘ−ｘ²＋ｘ³＋ｘ⁴＋ｘ⁵−ｘ⁶−ｘ⁷−ｘ⁸＋ｘ⁹＋ｘ¹⁰＋２（ｘ−ｘ¹⁰）
＝ｘ−ｘ²＋ｘ³＋ｘ⁴＋ｘ⁵−ｘ⁶−ｘ⁷−ｘ⁸＋ｘ⁹−ｘ¹⁰
＝ｘ＋ｘ³＋ｘ⁴＋ｘ⁵＋ｘ⁹−（ｘ²＋ｘ⁶＋ｘ⁷＋ｘ⁸＋ｘ¹⁰）

　そこで、　Ａ＝ｘ＋ｘ³＋ｘ⁴＋ｘ⁵＋ｘ⁹　、Ｂ＝ｘ²＋ｘ⁶＋ｘ⁷＋ｘ⁸＋ｘ¹⁰　とおくと、

　ｉ・ｔａｎ（３π/１１）＋ｉ・４ｓｉｎ（２π/１１）＝Ａ−Ｂ

　Ａ＋Ｂ＝ｘ＋ｘ²＋ｘ³＋ｘ⁴＋ｘ⁵＋ｘ⁶＋ｘ⁷＋ｘ⁸＋ｘ⁹＋ｘ¹⁰

すなわち、　１＋Ａ＋Ｂ＝１＋ｘ＋ｘ²＋ｘ³＋ｘ⁴＋ｘ⁵＋ｘ⁶＋ｘ⁷＋ｘ⁸＋ｘ⁹＋ｘ¹⁰
　　　　　　　　　　　　　＝（１−ｘ¹¹）/（１−ｘ）＝０

　　よって、　Ａ＋Ｂ＝−１

　また、ＡＢ＝（ｘ＋ｘ³＋ｘ⁴＋ｘ⁵＋ｘ⁹）（ｘ²＋ｘ⁶＋ｘ⁷＋ｘ⁸＋ｘ¹⁰）
　　　　　　＝ｘ³＋ｘ⁷＋ｘ⁸＋ｘ⁹＋１
　　　　　　　　　＋ｘ⁵＋ｘ⁹＋ｘ¹⁰＋１＋ｘ²
　　　　　　　　　　　　＋ｘ⁶＋ｘ¹⁰＋１＋ｘ＋ｘ³
　　　　　　　　　　　　　　　＋ｘ⁷＋１＋ｘ＋ｘ²＋ｘ⁴
　　　　　　　　　　　　　　　　　　＋１＋ｘ⁴＋ｘ⁵＋ｘ⁶＋ｘ⁸
　　　　　 ＝５＋２（ｘ＋ｘ²＋ｘ³＋ｘ⁴＋ｘ⁵＋ｘ⁶＋ｘ⁷＋ｘ⁸＋ｘ⁹＋ｘ¹⁰）＝５−２＝３

　よって、Ａ、Ｂは、２次方程式 ｔ²＋ｔ＋３＝０　の２つの解である。

　解の公式より、　ｔ＝（−１±ｉ）/２　で、　Ａ−Ｂ＝±ｉ

　すなわち、　ｉ・ｔａｎ（３π/１１）＋ｉ・４ｓｉｎ（２π/１１）＝±ｉ　より、

　　　　ｔａｎ（３π/１１）＋４ｓｉｎ（２π/１１）＝±

　明らかに、ｔａｎ（３π/１１）＋４ｓｉｎ（２π/１１）＞０　なので、

　　ｔａｎ（３π/１１）＋４ｓｉｎ（２π/１１）＝

が成り立つ。


（コメント）　代数的には示せたものの、これを初等幾何的に示すには、どんな図形を使えば
　　　　　　いいのだろう？難問ですね。


　DD++さんからのコメントです。（平成２８年５月２３日付け）

　一見確かに同じように見えますが、少し調べてみると実は（初等幾何程度の深さでは）別物
なのではないかと思います。というのは、wolfram先生の力を借りて似たような式を量産すると
以下のようになるのです。

　tan(π/3) - 4sin(π/3) = -　、tan(π/4) - 4sin(π/4) = -

　tan(π/6) - 4sin(π/6) = -1

　tan(π/7) - 4sin(2π/7) = -　、tan(2π/7) - 4sin(3π/7) = -
　tan(3π/7) - 4sin(π/7) =

　tan(π/9) + 4sin(π/9) = 　、tan(2π/9) - 4sin(2π/9) = -
　tan(4π/9) - 4sin(4π/9) =

　tan(π/11) + 4sin(3π/11) = 　、tan(2π/11) - 4sin(5π/11) = -
　tan(3π/11) + 4sin(2π/11) = 　、tan(4π/11) + 4sin(π/11) =
　tan(5π/11) - 4sin(4π/11) =

　tan(π/12) + 4sin(π/12) = 　、tan(5π/12) - 4sin(5π/12) =

　tan(π/18) + 4sin(π/18) = 1　、tan(5π/18) - 4sin(5π/18) = -1
　tan(7π/18) - 4sin(7π/18) = 1

　よく見ると、これらの式は似たような二系統が混在しており、

(A) 分母の素因数が2と3のみである場合
　・・・tanとsinで角度は共通。tanの前にも係数がつくことがある。登場する平方根は±
　　　と±のみ。

(B) 分母が（何らかの性質を持つ）素数である場合
　・・・tanとsinで角度は異なる。tanの前に係数がつかない。登場する平方根は分母の平方
　　　根のみ。

　/9は(A)でたまたまtanに係数がつかなかっただけで、/11は(B)。もっと掘り下げれば多分
共通の理論等も言えるのだろうと思いますが、初等幾何で同じように考えるというのはかな
り厳しい道だと感じました。

　参考として、/9の3つの式の初等幾何学的証明を投稿しておきます。

(1)　tan(π/9) + 4sin(π/9) =

　AB=2、∠A=π/3、∠B=π/6、∠C=π/2 の直角三角形ABCを考える。辺BC上に点 D、E

を取り、∠Aを三等分、すなわち、∠BAD=∠DAE=∠EAC=π/9 とする。

　点Bから線分ADの延長に垂線BFを下ろし、線分BFの延長と線分AEとの交点をGとする。

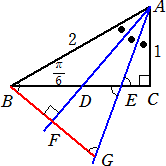直角三角形ABFに注目すると、BF=ABsin(π/9)=2sin(π/9) 　　　　△ABF≡△AGF より、BG=2BF=4sin(π/9) 　∠EGB=∠ABF=7π/18=∠AEC=∠BEG より、BE=BG=4sin(π/9) 　　また、AC=ABsin(π/6)=1 なので、EC=ACtan(π/9)=tan(π/9) よって、 tan(π/9)+4sin(π/9)=EC+BE=BC=ABcos(π/6)=

(2)　tan(2π/9) - 4sin(2π/9) = -

　AC=2、∠A=π/6、∠B=5π/18、∠C=5π/9 の三角形ABCを考える。辺BCの延長（C方

向）上に CD=2 となる点Dをとり、点Cから線分ABおよびADに垂線CEおよびCFを下ろす。

　AC=CD=2 および ∠ACD=4π/9 より、∠ACF=∠DCF=2π/9　なので、AD=4sin(2π/9)

　∠ADC=π/2-∠DCF=5π/18=∠B より、　AB=AD=4sin(2π/9)

　また、CE=ACsin(π/6)=1 なので、BE=CEtan(2π/9)=tan(2π/9)

　よって、tan(2π/9)-4sin(2π/9)=BE-AB=-AE=-ACcos(π/6)=-

(3)　tan(4π/9) - 4sin(4π/9) =

　AB=2、∠A=π/3、∠B=π/6、∠C=π/2 の直角三角形ABCを考える。辺BCの延長（B方

向）に ∠CAD=4π/9 となる点Dをとる。線分ADの延長（A方向）に AE=2 となる点Eをとる。

点Aから線分BEに垂線AFを下ろす。

　AB=AE=2 および ∠BAE=π-(∠CAD-∠CAB)=8π/9 より、∠BAF=∠EAF=4π/9

　よって、BE=4sin(4π/9)

　∠EDB=π/2-∠CAD=π/18=π/2-∠EAF=∠DEB より、BD=BE=4sin(4π/9)

　また、AC=ABsin(π/6)=1 なので、CD=ACtan(4π/9)=tan(4π/9)

　よって、tan(4π/9)-4sin(4π/9)=CD-BD=BC=ABcos(π/6)=


＃これらを参考に/11をやろうとするなら、まずをどこから生み出すかという課題をクリ
　アしないといけません。

　　sin(π/11)sin(2π/11)sin(3π/11)sin(4π/11)sin(5π/11)=/32

つまり、半径1の円に内接する正11角形の辺及び4つの異なる長さの対角線の総乗が
というのはありますが、これを今回に使えるかも、そもそもこれを初等幾何で証明できるかも
謎ですね。


　空舟さんからのコメントです。（平成２８年５月２４日付け）

　次のように一般化できました。

【命題】　pを4N+3型素数としてθ=2π/pとおく。pを法とする平方剰余について、0以上p-1以
　　　　下で代表系をとったときに、4を法として2か3に合同な集合をAとすると、

　　tan(θ) - Σ[a∈A] 4sin(aθ) = -√p が成り立つ

例　p=19 では、　tan(θ)-4sin(6θ)-4sin(7θ)-4sin(11θ) = -√19

　　p=23 では、　tan(θ)-4sin(2θ)-4sin(3θ)-4sin(6θ)-4sin(18θ) = -√23

[考察過程]　z=exp(2πi/p)とおくと、(z-1/z)/(z+1/z) = Σc[k]z^k

　　　　　　　　　ただし、k≡0,1 (mod 4) のとき c[k]=1、他の時 c[k]=-1

　一方、ガウス和により、　√-p = Σd[k]z^k

　　　　　　　　　ただし、kが平方剰余のときd[k]=1, 他の時 d[k]=-1

　これらを比較して観察しました。


　DD++さんからのコメントです。（平成２８年５月２４日付け）

　情報ありがとうございます。19や23も4sinを2セットか3セット作ればいけそうだとは思ってい
ましたが、具体的な式までは手が回りませんでした。

　問題は、これを初等幾何で証明できるのかですが……。


　ＧＡＩ さんからのコメントです。（平成２８年５月２５日付け）

　ガウス和に結びついているなんて思ってもいませんでした。

　p=83 なら、

tan(θ)-4sin(3θ)-4sin(7θ)-4sin(10θ)-4sin(11θ)-4sin(23θ)-4sin(26θ)-4sin(27θ)
　-4sin(30θ)-4sin(31θ)-4sin(38θ)-4sin(51θ)-4sin(59θ)-4sin(63θ)-4sin(70θ)
　　-4sin(75θ)-4sin(78θ) = -√83　　（なおθ=2*π/83）

が成立すると言うわけですね。こんなこと見えるわけありません。

　4N+1型の素数に対する類似の一連の式は何かありませんか？