当HPでは、作図題について、いろいろな条件を与えて考察してきた。(→基本の作図 )
そこでは、定木(2点を結ぶ線分の作図が可能)、コンパス(1点を中心とする円の作図
が可能)を巧妙に利用している。
最近、定木・コンパスを用いないで、定長線分(マッチ棒をイメージすればいいかな?)を
用いて、同様の作図が可能であることを知る機会があった。
チェスの問題作成者で有名なT.R.ドーソンが発見したという。定木・コンパスで作図でき
ないものは定長線分を用いても出来ないとのことである。
使っていいのは、長さが一定な線分
以下では、この長さを 1 として考えることにする。
まず、この線分を用いて出来ることを列挙してみよう。
基本の操作
(A) 線分は、平面上のどこでも自由に置くことも取り去ることもできる。
(B) 2定点を端点として、2つの線分で二等辺三角形を作ることができる。
(C) 線分の長さより短い距離にある2定点を線分で結ぶことができる。
(D) 直線からの距離が線分より短い点を端点として、線分の残りの端点を直線上
におくことができる。
これらの基本の操作を踏まえて、次の作図を考えてみよう。
(1) 線分の延長
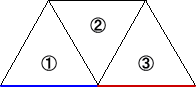
上図のように、青い線分を出発して、正三角形(①→②→③)を作りながら、赤い線分
が作図できる。これは青い線分の延長になっている。
(2) 垂線
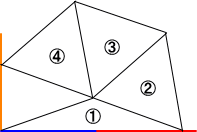
上図のように、青い線分を延長して、その上に適当に二等辺三角形(①)を作る。二等
辺三角形の等辺の一方を、正三角形(②→③→④)を作りながら延長する。このとき、延
長の端点ともとの端点を結ぶと、それは垂線になっている。
(コメント) これは、直角三角形の外接円の中心は斜辺の中点であるという事実に基づく。
(3) 平行線

上図のように、青い線分を出発して、正三角形(①→②)を作りながら、赤い線分が作図
できる。これは青い線分と平行である。
ただし、平行線の間の距離は、
(4) 直線外の定点からの垂線
直線外の定点と直線との距離が 1/2 以上の場合は、(1)(3)を用いて、点と直線との
距離を 1/2 より小にできるから、初めから直線外の定点と直線との距離は 1/2 より小
として考えてもよい。
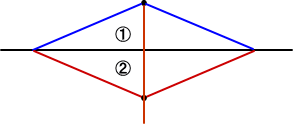
上図のように、定点を端点とする二等辺三角形(①)を作ると、下側の二等辺三角形(②)
も自動的に定まる。この2つの頂点を結べば、所要のものが得られる。
(5) 線分の中点
2点間の距離が 2 ならば、(1)の方法により、直ちに中点は定まる。2点間の距離が 2
より大ならば、やはり、(1)の方法により、2点それぞれを端点として同じ回数、線分を延
長し、2つの端点間の距離を 2 より小にできるので、初めから2点間の距離は 2 より小
として考えてもよい。
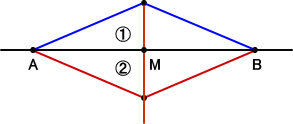
(4)と同様の考えで、A、Bを端点とする二等辺三角形(①、②)を作る。この2つの頂点
を結ぶ線分と線分ABの交点が求める点である。
(ここでは、線分ABは与えられるものとする。2点A、Bから線分ABを作図する方法は後
で述べることにする。)
(6) 線分の垂直2等分線および角の2等分線
次の図をじっと眺めていると、その作図法は理解されるだろう。

(7) 直線外の定点を通る平行線
(3)の方法を繰り返し用いることにより、初めから、与えられた点と直線との距離は 1
より小としてよい。

上図のように、平行四辺形を作る要領で、所要のものが得られる。
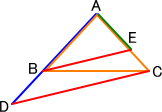
(8) 2点A、Bを結ぶ線分

上図のように、2点A、Bから線分を引き、交点をCとする。線分AC、BCの中点をそれ
ぞれM、Nとおく。2点M、N間の距離が1より大きい場合は、さらに、MC、NCの中点を
とればよいから、初めから2点M、N間の距離は 1以下として考えてもよい。
このとき、(7)の方法により、2点A、Bを結ぶことが出来る。
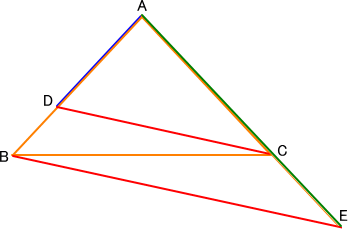
(9) 定められた長さの線分
あらかじめ与えられた長さの線分を、任意の直線上の任意の位置に引くことを考える。
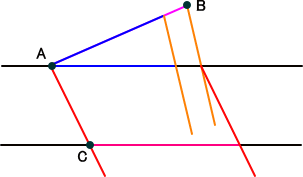
いま、与えられた長さをもつ線分を AB とし、平面上の任意の点 C と、その点を通る任
意の直線が与えられている。
点 C を通る直線に平行で、点Aを通る直線を引くことが出来る。(←(7)) そこで、その
平行線と線分 AB 上に長さ 1 の線分をとり、端点を結ぶ。(←(8)) その直線に平行で
点 B を通る直線が引ける。(←(7)) その直線と点 A を通る平行線との交点が定まる。
2点 A、C を結び(←(8))、その直線に平行で、上述の交点を通る直線を引くことが出来
る。(←(7)) その直線と初めに与えられた点 C を通る直線との交点を求めれば、所要
の結果を得ることが出来る。
(10) 線分の分点
線分の内分点の作図方法を考える。外分点も内分点と同様に求められる。

与えられた線分ABにおいて、点Aより任意に直線AXを引く。その直線上において、定長
線分を何本か用いて、内分点を求める。(図では、1:2 に内分する場合)
2点CとBを結び(←(8))、点Dより、線分CBに平行な直線を引き(←(7))、線分ABとの
交点Pを求める。点Pは、線分ABを分ける点である。
(11)平方数の作図
与えられた長さ n の平方数 n2 の作図方法を考える。