切片を求める　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

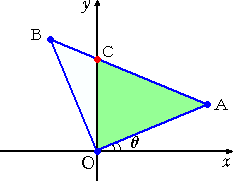
右図は、直角をはさむ２辺の長さがそれぞれ １ の直角２等辺三角形ＯＡＢを原点の周りに角 θ だけ回転させたものである。 　ただし、０＜θ＜π/２　とする。 　そこで、△ＯＡＣの面積を求めたいのだが、ど うしてもＯＣの長さが必要である。 　ＯＣの長さを求める方法としていくつか考えら れるので、ここで整理しておきたいと思う。

（最も易しいと思われる解法・・・面積の利用）

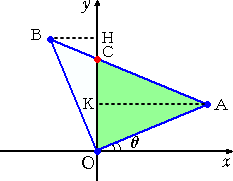　　２点Ａ、Ｂより、ｙ 軸に垂線ＡＫ、ＢＨを下ろす。
　このとき、　ＡＫ＝ｃｏｓθ　、ＢＨ＝ｓｉｎθ　なので、

　　△ＯＡＢ＝△ＯＡＣ＋△ＯＢＣ
　　　　　　　＝ＯＣ×（ｓｉｎθ＋ｃｏｓθ）/２

　　△ＯＡＢ＝１/２　なので、

　　　　ＯＣ＝１/（ｓｉｎθ＋ｃｏｓθ）



　この問題を考えたとき、最初上記の解法が思い浮かばず、次のような方法で求めてしま
った。（今から考えると、ちょっと強引でした！）

（ベクトルを用いた解法）

　＝（ｃｏｓθ、ｓｉｎθ）　、　＝（−ｓｉｎθ、ｃｏｓθ）　より、

　　＝（−ｓｉｎθ−ｃｏｓθ、ｃｏｓθ−ｓｉｎθ）

　ここで、　 と は平行なので、＝ｋ　（ｋ は実数）　とおける。

よって、　＝＋＝（ｃｏｓθ−ｋ（ｓｉｎθ＋ｃｏｓθ）、ｓｉｎθ＋ｋ（ｃｏｓθ−ｓｉｎθ））

点Ｃの ｘ 座標は、０ であるから、　　ｃｏｓθ−ｋ（ｓｉｎθ＋ｃｏｓθ）＝０

　これより、　ｋ＝ｃｏｓθ/（ｓｉｎθ＋ｃｏｓθ）　となるので、点Ｃの ｙ 座標は、

　ｓｉｎθ＋ｋ（ｃｏｓθ−ｓｉｎθ）＝ｓｉｎθ＋ｃｏｓθ（ｃｏｓθ−ｓｉｎθ）/（ｓｉｎθ＋ｃｏｓθ）

　　　　　　　　　　　　　　　　　　＝１/（ｓｉｎθ＋ｃｏｓθ）

となることが分かる。

　また、直線の方程式を直接回転させて求めることもできる。

（回転移動の利用）

　直線の方程式　ｘ＋ｙ＝１　を原点の周りに角 θ だけ回転させて出来る直線が直線ＡＢで
ある。

　ｘ＋ｙ＝１　上の点（ｘ、ｙ）を原点の周りに角 θ だけ回転させて出来る点を（Ｘ、Ｙ）とすると、

　　　ｘ＝Ｘｃｏｓθ＋Ｙｓｉｎθ　、　ｙ＝−Ｘｓｉｎθ＋Ｙｃｏｓθ

なので、ｘ＋ｙ＝１　に代入して整理すると、

　　　　　　　　　　　Ｘ（ｃｏｓθ−ｓｉｎθ）＋Ｙ（ｓｉｎθ＋ｃｏｓθ）＝１

ここで、　Ｘ＝０　とおいて、　Ｙ＝１/（ｓｉｎθ＋ｃｏｓθ）

　回転移動を用いないで、直接的に直線ＡＢの方程式を求めて点Ｃの座標を求めてもよい。

（直線の方程式による直接的な解法）

　Ａ（ｃｏｓθ、ｓｉｎθ）、Ｂ（−ｓｉｎθ、ｃｏｓθ）なので、２点Ａ、Ｂを通る直線の方程式は、

　　（ｓｉｎθ＋ｃｏｓθ）（ｙ−ｓｉｎθ）＝（ｓｉｎθ−ｃｏｓθ）（ｘ−ｃｏｓθ）

ここで、　ｘ＝０　とおいて、　（ｓｉｎθ＋ｃｏｓθ）ｙ＝（ｓｉｎθ＋ｃｏｓθ）ｓｉｎθ−（ｓｉｎθ−ｃｏｓθ）ｃｏｓθ

より、　　（ｓｉｎθ＋ｃｏｓθ）ｙ＝１　となり、　ｙ＝１/（ｓｉｎθ＋ｃｏｓθ）　が言える。

（直線の方程式による直接的な解法・・・ヘッセの標準形の利用）

　２点Ａ、Ｂを通る直線の方程式は、ヘッセの標準形より、

　　　　　　ｘｃｏｓ（θ＋４５°）＋ｙｓｉｎ（θ＋４５°）＝１/

このとき、　ｘ（ｃｏｓθ−ｓｉｎθ）＋ｙ（ｓｉｎθ＋ｃｏｓθ）＝１

よって、　　ｙ 切片は、　（ｓｉｎθ＋ｃｏｓθ）ｙ＝１　より、　ｙ＝１/（ｓｉｎθ＋ｃｏｓθ）　

（コメント）　単なる切片の長さを求めるのだが、いろいろな考え方が可能で、数学の面白さ
　　　　　　が伝わってくるような問題である。因みに、問題の出典は、武蔵工業大学の入試
　　　　　　問題である。

　　　これまで何十人と、世に難関大学と言われるところの東大・京大等に入学した生徒達
　　を指導してきたが、彼らに共通することは、定石と言われる上手い方法で計算すること
　　はあまりなく、彼ら独自の言葉で考え、答えを導き出しているという点である。

　　　当ＨＰの読者の方も、今現在、受験勉強に身を置いている人も多いと思う。上手い手
　　は時間とともに忘れるが、自分で考え出した方法は身体が覚えていて決して忘れない。
　　そのことを念頭に置いて、受験勉強に励んでほしいと思う。（塾長）

（追記）　平成１８年８月７日付けで、ＨＮ：「かず」さんという当ＨＰの読者の方からメールを
　　　　頂いた。

　かずさんによれば、「△ＯＡＣ に対して、正弦定理を用いると、すぱっと ＯＣ の長さが求ま
る。」とのことである。

実際に、ＯＡ＝１　で、∠ＯＣＡ＝θ＋４５°、∠Ａ＝４５° なので、正弦定理より、 　　　　　　　 　ここで、 　　　　 　よって、 　　　　　　　　ＯＣ＝１/（ｓｉｎθ＋ｃｏｓθ）

　「この問題を高３生に解かせると、大抵の場合、直線の方程式を直接求めにいって大変
なことになるみたいです。」と、かずさん。確かに、この単純な「 ｙ 切片を求める」問題に対
して、私自身も生徒に質問されて咄嗟に思いついた解法は、ベクトルを利用するもので、
面積や正弦定理を用いる軽妙な方法は思い浮かばなかった．．．(^^;)。

　冒頭の問題に限って言えば、解法の易しさという点で、正弦定理を利用したものに比べ、
面積を利用した方が優れていると思う。かずさんは次のような問題を意識されて、正弦定
理を利用して機械的にさくっと長さを求める方法を思い浮かばれたようだ。

　　面積計算で行う場合は，直角だからこそ簡単にできたと思う。もし、あの角が ６０度や
　１２０度なら、どうだろうか？実は、１２０度になっている場合が過去に入試で出題された
　ことがある。次のような問題である。

　　　『 原点を中心とする半径 １ の円が座標平面上にある。この円に内接する正三角
　　　　形を原点を中心に回転させるとき、この正三角形の第１象限にある部分の面積
　　　　の最小値と最大値を求めよ。　　　　（平成１３年度　岡山大学　前期（全学）　　』

　原点がちょうど正三角形の外心（または重心）であることに、まず注意しよう。

　この問題に対して咄嗟に浮かぶ私の解法はヘッセの標準形を利用するものである。

　正三角形と第１象限との共通部分は、直角三角形または四角形の２つの場合がある。

　π/６≦θ≦π/３　のとき、
　　　　　　　　　　

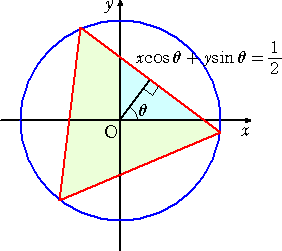
　π/３≦θ≦５π/６　のとき、
　　　　　　　　　　

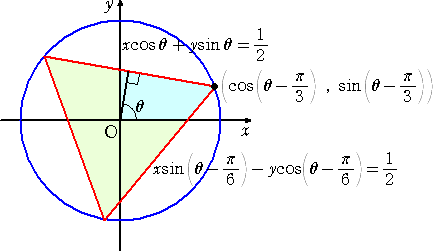
　上図から共通部分の面積を求めて、その取り得る値の範囲を求めることは容易だろう。

　かずさんは、この問題に正弦定理を利用されるとのことであるが、どのような解法になる
のだろうか？大いに興味あるところである。このような新しい視点からの再考の機会を与
えていただいた、かずさんに感謝いたします。（→　正弦定理の利用方法）

（追々記）　上記で、「取り得る値の範囲を求めることは容易だろう。」と、計算もしないで言
　　　　　　ってしまったが、実際に計算してみると意外にハードな計算であることを思い知ら
　　　　　　された。（河合塾の難易度レベルでは、「やや難」だという！）

（問題の解答）　求める部分の面積を、Ｓ とおく。

　π/６≦θ≦π/３　のとき、
　　　　　　　　　　　　　　　　　　

　　　π/３≦２θ≦２π/３　なので、　　/２≦ｓｉｎ２θ≦１

　　よって、　　　１/４ ≦ Ｓ ≦ /６　である。

　π/３≦θ≦５π/６　のとき、

　　　　
　　　　　

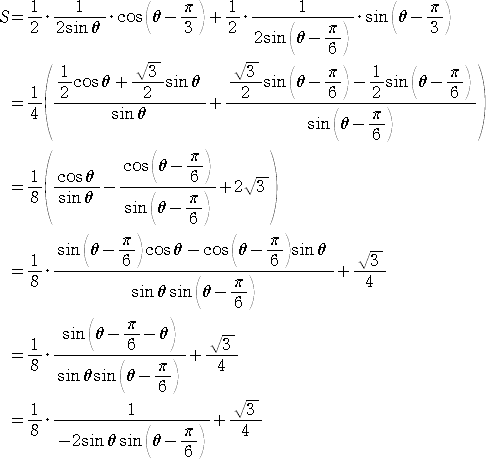
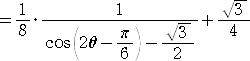
　　　π/２≦２θ−π/６≦３π/２　なので、　　−１≦ｃｏｓ（２θ−π/６）≦０

　　よって、　（１/８）（−２/）＋/４ ≦ Ｓ ≦ （１/８）（−２/（２＋））＋/４　より、

　　　　　　　　/６ ≦ Ｓ ≦ （−１）/２

　以上から、Ｓ の取り得る値の範囲は、　　１/４ ≦ Ｓ ≦ （−１）/２　　なので、

　最小値は、　１/４　（θ＝π/４ のとき）、最大値は、 （−１）/２　（θ＝７π/１２ のとき）

となる。（終）

（追々々記）　平成１８年８月１４日付けで、かずさんよりメールを頂いた。お忙しい中、詳し
　　　　　　　　い説明をいただき、感謝いたします。
　　　　（いただいた原稿は、かずさんの手書きによるもので、とてもきれいにまとめられていました！）

　正弦定理を用いても、基本的な計算手法は上記で述べたものとあまり変わらない。多少
上記の計算より、計算が煩雑になるかな？くらいの差である。

　ヘッセの標準形は、最初の偏角θの設定に慣れないと難しいかもしれないが、後々の計
算を楽にしてくれる。

　それに対して、正弦定理を用いる場合は、最初の偏角θの設定は、ごく自然であるが、そ
の分、後の計算は、ちょっと大変なようである。（私の個人的な感想！）

　かずさんからは詳しい解答をいただいたが、上記の理由から、正弦定理の使い方までを
説明するにとどめたいと思う。以下は、かずさんよりいただいた原稿の一部である。
（一部文言等は修正させていただきました。）

　正三角形の１つの頂点Ａの座標が、　（ ｃｏｓθ ， ｓｉｎθ ）　（０≦θ＜２π/３） と表されるものと
する。

　０＜θ＜π/２　のとき、下図のように、正三角形と第１象限との共通部分は、四角形ＯＰＡＱ
となる。

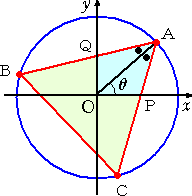	△ＡＯＰにおいて、正弦定理より、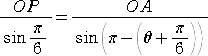 　　　　　　 　　　　よって、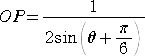
同様にして、△ＡＱＯにおいて、正弦定理より、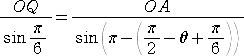 　　　　　　 よって、 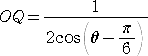　　　　　　　　 となる。

θ＝０　、π/２　のときはそれぞれ　△ＡＱＯ　、△ＡＯＰ　を利用すればよい。

　π/３≦θ≦５π/６　のとき、下図のように、正三角形と第１象限との共通部分は、△ＯＰＱ
となる。

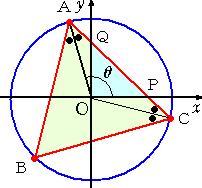	△ＡＯＱにおいて、正弦定理より、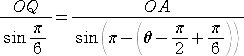 　　　　　　 　　　　よって、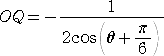
同様にして、△ＣＰＯにおいて、正弦定理より、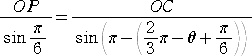 　　　　　　 よって、 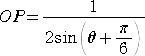　　　　　　　　 となる。

（コメント）　上記で得られたＯＰ、ＯＱを用いて面積を出し、その最大値・最小値を求める
　　　　　　ことは前述とほぼ同じである。出来るだけ、ＯＰ、ＯＱを易しい表現の式に直して
　　　　　　おくと、後々の計算が楽なような．．．予感！


（追記）　甲府市在住の当ＨＰ読者の方から「垂線を下ろすことの良さ」について、メールをい
　　　　ただいた。（平成２９年１２月３日付け）

　大学入試の数学を勉強している際、たまに二等辺三角形を扱う問題に遭遇する。その際、
必ずといっていいほど、垂線を下ろしていた。
（AB＝ACの二等辺三角形ABCの頂点A から垂線をおろすこと）

　なぜかと言うと、垂線下ろすと、大体上手くいっていたからだ。解答では、よく正弦定理が
用いられて、簡潔にかかれていたが、自分は正弦定理が嫌いだったため（余弦に比べ影
が薄く、受験生の意識の外をぽっとつくような定理であり、困ったら正弦定理を使え！と、
数学の先生からテクニック的なものとして押し付けられたため。そんなものは意識の外で、
毎回垂線を引いていた。

　そんな記憶を蘇らせてくれたのが冒頭の問題である。

　たいして考えもせず、ぼーっと答えを眺めていたが、そこで直角二等辺三角形の問題であ
り、正弦定理の解法をみる。これは、垂線下ろせば、いけるんではないかと、ペンを動かす
と、やっぱりいけた。

（解答）　対称性より、0＜θ≦π/4　について考えればよい。OからABに向かって垂線の足

　Hを下ろすと、OH=1/√2　で、また、∠COH =π/4−θ　より、OC×cos（π/4−θ）=OH

　なので、　OC=1/（sinθ+cosθ）


＃　やっぱりいけた！

　当時、予備校の先生に聞いたところ、垂線を下ろすってことは、原点回帰してるみたいな
ことで、定理もそこから導き出されてるから、みたいな答をいただいた。そこで調べた正弦
定理の証明では、垂線を下ろしていたので、「なんだよ、正弦定理じゃなくて、垂線下ろせば
いいじゃん。てか、むしろこっちが本流じゃね？」みたいに思った記憶がある。

　長文大変失礼いたしました。既に思い付いておられるかとは思いますが、正弦定理じゃな
くて、垂線下ろせば解けるんだぞ！原始的な方法でもいけるんだ！って思いが、この問題を
通じてふつふつと蘇ってきて、ここまで書いてしまいました。



　　　　以下、工事中