意外な所に２等辺三角形　　　　　　　　　　　　　　　　　　

　小学校５年生で２等辺三角形のいろいろな性質を学んで以降、与えられた図形の中に
２等辺三角形を見い出し、その性質から問題が解決されるということは多分多くの人が経
験していることだろう。

　幾何の問題において、補助線の発見と同様に、隠れた２等辺三角形を探すことも一つの
着眼のポイントとなる。

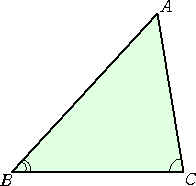
　例　左図のような△ＡＢＣにおいて、

　　　　　ＡＢ＞ＡＣ　ならば、　∠Ｃ＞∠Ｂ　である。

　　この事実は、「三角形の最大辺には最大角が対応する」
　ことを示すのに用いられるが、２等辺三角形の効果を知る
　最良の問題と言える。

　　証明は易しいだろう。

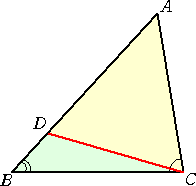
（証明）　右図のように、ＡＤ＝ＡＣ となるように、辺ＡＢ上 　　　に点Ｄをとる。このとき、△ＡＤＣは２等辺三角形。 　　　よって、　∠ＡＣＤ＝∠ＡＤＣ　である。 　　　このとき、　∠Ｃ＝∠ＡＣＤ＋∠ＢＣＤ 　 　　　　　　　　　　　＝∠ＡＤＣ＋∠ＢＣＤ 　　　　　　　　　　　　 ＝∠Ｂ＋２∠ＢＣＤ＞∠Ｂ （証終）

　次の問題は意外な所に２等辺三角形が見い出され、その結果として興味ある性質を導く
ことができる。

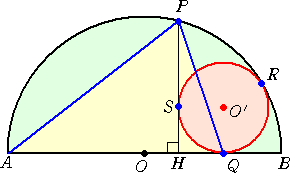
　左図のような半径 ａ の半円に半径 ｒ の円Ｏ’
が内接している。

　直径ＡＢに垂直な円Ｏ’の接線と半円との交
点をＰとし、接点をＱ、Ｒ とする。

　このとき、△ＡＰＱ は２等辺三角形である。



（証明）　右図において、ＯＨ＝ｈ　とおく。

　　　　このとき、　ＡＰ²＝（ａ＋ｈ）²＋ａ²−ｈ²＝２ａ²＋２ａｈ

また、円Ｏ’が半円に接しているので、　（ａ−ｒ）²＝（ｈ＋ｒ）²＋ｒ²　　より、　

　　　　　　　　　　　２（ａ＋ｈ）ｒ＋ｒ²＝ａ²−ｈ²

よって、ＡＱ²＝（ａ＋ｈ＋ｒ）²＝（ａ＋ｈ）²＋２（ａ＋ｈ）ｒ＋ｒ²＝（ａ＋ｈ）²＋ａ²−ｈ²＝２ａ²＋２ａｈ

したがって、ＡＰ²＝ＡＱ²　即ち、ＡＰ＝ＡＱ　となり、△ＡＰＱ は２等辺三角形である。（証終）


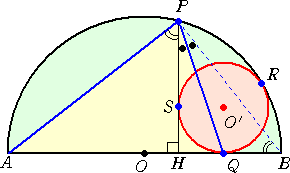
　　△ＡＰＱ が２等辺三角形であることから、

　直ちに、

　　　　　線分ＰＱは∠ＢＰＨの２等分線

　であることが分かる。



　実際に、　△ＡＰＱ が２等辺三角形であることから、　∠ＡＰＱ＝∠ＡＱＰ

　　　　　ここで、　∠ＡＰＱ＝∠ＡＰＨ＋∠ＨＰＱ　、　∠ＡＱＰ＝∠ＰＢＱ＋∠ＢＰＱ　なので、

　　　　　　　　　　　∠ＡＰＨ＝∠ＰＢＱ　より、　∠ＨＰＱ＝∠ＢＰＱ

　　　　　よって、　線分ＰＱは∠ＢＰＨの２等分線である。


（追記）　平成２１年９月６日付け

　平成２１年９月４日付けで当ＨＰの掲示板「出会いの泉」にＨＮ「凡人」さんが面白い問題を
提示された。

問　題　△ＡＢＣにおいて、ＡＢ＝２、ＢＣ＝４、ＣＡ＝３　とする。辺ＢＣ上に、ＡＤ＝ＤＣ

　　　　となるように点Ｄを取るとき、ＡＤの長さを求めよ。

　問題自体は高校１年レベルで容易に解き得る。余弦定理を用いればよい。

　　実際に、左図において、余弦定理より、

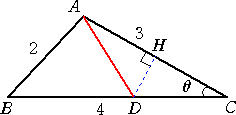　　　ｃｏｓθ＝７/８

なので、

　　　ＡＤ＝（３/２）（１/ｃｏｓθ）＝１２/７



　これに対して、「凡人」さんが注目しているのは、この問題が「余弦定理や三平方の定理な
どを使わない」形で、小学生レベル（この場合は私立中学受験レベルを想定）で解き得るか
という点である。

　この凡人さんの問いかけに対して、当ＨＰがいつもお世話になっているＨＮ「らすかる」さん
が、発問からわずか２時間１５分後に十分小学生的と思われる鮮やかな解法を示された。


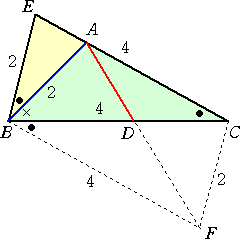
　　ＣＥ＝ＣＢ＝４、ＥＢ＝２ である二等辺三角形ＣＥＢ
　において、ＡＢ＝２となるようにＣＥ上に点Ｅと異なる
　点Ａをとる。

　　△ＣＥＢ∽△ＢＡＥから、ＡＥ＝１　となり、ＣＡ＝３

　　よって、△ＡＢＣは問題にある三角形である。

　　次に、四角形ＣＥＢＦが平行四辺形になるように
　点Ｆをとる。

　　このとき、明らかに、△ＣＥＢ≡△ＢＦＣ　である。


　また、　ＢＣ＝ＦＢ＝４　、　ＣＦ＝ＥＢ＝ＢＡ＝２　で、

∠ＦＢＡ＝∠ＦＢＣ＋∠ＣＢＡ＝∠ＢＣＡ＋∠ＣＢＡ＝∠ＥＢＡ＋∠ＣＢＡ＝∠ＣＢＥ＝∠ＢＣＦ

より、２辺とその間の角が相等しいので、　△ＢＦＣ≡△ＦＡＢ　となる。

　このとき、ＡＦとＢＣの交点をＤとすると、明らかに、　ＡＤ＝ＤＣ　で、

　　　ＡＤ ： ＤＦ ＝ ＡＣ ： ＢＦ ＝ ３ ： ４

となる。

　したがって、　ＡＤ＝（３/７）ＡＦ＝１２/７　となる。

（コメント）　らすかるさんの解答は、２等辺三角形の性質を上手く用いられていますね！
　　　　　　感動的です。らすかるさんに感謝します。

　最初に「２等辺三角形ありき」で、その途中で題意を満たす△ＡＢＣが出現するという手法
は、私にとって多分初めて見る解法です。

　らすかるさんの解法を参考にしながら題意を満たす△ＡＢＣを出発点として、ＡＤの長さを
求めるための道筋を考えてみよう。

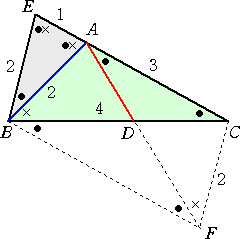題意を満たす△ＡＢＣに、左図のような２等辺三角 　形ＡＢＥを付加する。 　　明らかに、３点 Ｅ、Ａ、Ｃ は一直線上にある。 　　さらに、△ＡＢＣと合同な△ＣＦＡを左図のように付 　加すると、ＢＦとＡＣは平行となるので、 　　　　　　∠ＢＣＡ＝∠ＢＦＡ 　　よって、　△ＥＢＣ≡△ＡＢＦ　となり、　ＢＦ＝４ 　このとき、　ＡＤ ： ＤＦ ＝ ＡＣ ： ＢＦ ＝ ３ ： ４　より、 　　　　ＡＤ＝（３/７）ＡＦ＝１２/７

（コメント）　らすかるさんの解法を模倣しましたが、やはり２等辺三角形の性質が本質的に
　　　　　　効いていて、その呪縛から逃れることは出来ませんでした！

　また、ほとんど小学生的ではないが、ＨＮ「ロン」様（９月５日付け）のように、面積比に注目
して解かれた方もおられる。

　ＡＤ＝ｄ　とおくと、　△ＡＢＤ ： △ＡＤＣ ＝ ４−ｄ ： ｄ　より、

　　　（４−ｄ）△ＡＤＣ＝ｄ△ＡＢＤ　すなわち　（４−ｄ）²（△ＡＤＣ）²＝ｄ²（△ＡＢＤ）²

　ヘロンの公式より、

　　　（△ＡＢＤ）²＝３（３−ｄ）（ｄ−１）　、　（△ＡＤＣ）²＝（９/４）（ｄ＋３/２）（ｄ−３/２）

なので、　　（４−ｄ）²・（９/４）（ｄ＋３/２）（ｄ−３/２）＝ｄ²・３（３−ｄ）（ｄ−１）

すなわち、　２８ｄ⁴−１６０ｄ³＋２１３ｄ²＋２１６ｄ−４３２＝０

　この方程式は、　ｄ＝１２/７　（←　見つけるのが大変かも．．．。）を解に持ち、さらに、

　　　　　　　　　　

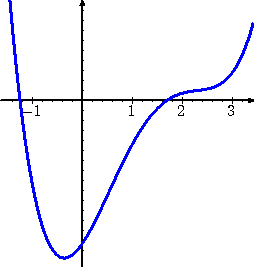
から、題意を満たす ｄ の値は、　ｄ＝１２/７　のみである。

（コメント）　４次方程式の解は、グラフを用いないと辛いですね！グラフから、一発で、
　　　　　　「１２/７」（←　±１０８の約数/７の約数　から候補を選ぶ！）と見当がつくかな。