大学院入試問題集　解答編

問題　１　（京都大学）　の解答例（目次に戻る）

　まず、（２）を証明する。（１）は、この（２）より明らかとなる。

　題意より、Ｆ は全単射で、また、連続性から、単調関数である。
いま、Ｆ は、単調増加であると仮定する。
　条件 Ｆ≠ Ｉ により、Ｆ(Ｘ)≠Ｘ となる Ｘ が存在し、Ｆ(Ｘ)＞Ｘ　または　Ｆ(Ｘ)＜Ｘ　が成り立つ。
　Ｆ(Ｘ)＞Ｘ　とすると、Ｘ＝Ｆ・Ｆ(Ｘ)＞Ｆ(Ｘ)　となり、これは、Ｆ が、単調増加であることに矛盾。
　Ｆ(Ｘ)＜Ｘ　としても、同様に矛盾を得る。したがって、Ｆ は、単調減少である。
このとき、Ｇ(Ｘ)＝Ｘ−Ｆ(Ｘ)　とおくと、Ｇは連続で、
　十分小さい全てのＸに対して、Ｇ(Ｘ)＜０　で、十分大きい全てのＸに対して、Ｇ(Ｘ)＞０
となることから、中間値の定理により、
　　　　　　　Ｇ（ａ）＝０　すなわち、ａ＝Ｆ(ａ)　となる ａ が存在する。
そこで、写像 φ 、ψ を次のように定義する。

　　　　　　　　

　このとき、簡単な計算により、φ・ψ ＝ Ｉ 、ψ・φ ＝ Ｉ　となるので、φ は全単射である。
また、φ 、ψ の定義から、明らかに φ 、ψ は連続である。よって、 φ は、Ｒ から Ｒ への位相
同型写像となる。このとき、ψ＝φ^-1　であるので、
　　Ｘ≧０ のとき、φ・Ｆ・φ^-1(Ｘ) ＝ φ・Ｆ(Ｘ＋ａ) ＝ ａ−Ｆ・Ｆ(Ｘ＋ａ) ＝ ａ−(Ｘ＋ａ) ＝ −Ｘ
　　Ｘ≦０ のとき、φ・Ｆ・φ^-1(Ｘ) ＝ φ・Ｆ(Ｆ(ａ−Ｘ)) ＝ φ(ａ−Ｘ) ＝ ａ−Ｘ−ａ ＝ −Ｘ
を得る。したがって、φ・Ｆ・φ^-1 ＝ −Ｉ　が成り立つ。以上で、（２）が示された。

次に、（１）について、
　Ｆ(Ｘ)＝１−Ｘ　なので、Ｘ＝Ｆ(Ｘ)＝１−Ｘ　を解けば、Ｘ＝1/２≡ａ　である。
したがって、φ(Ｘ)＝Ｘ−1/２　とすればよい。（終）

（参考図）　上の問題で考えられた写像を図式化すれば、下図のようになる。

　　　　　

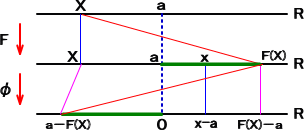
　　　φ は、ａ を境として、左側の目盛を変える働きをすることが分かる。

問題　２　（東京教育大学（現　筑波大学））　の解答例（目次に戻る）

　命題は、真である。
　いま、Ｍが上に有界でないとすると、任意の自然数 ｎ に対して、ｎ ＜Ｘｎ　となるＭの要素
Ｘｎ が存在する。このとき、Ｍの部分集合｛Ｘｎ｜ｎ≧１｝は最大数を持たないので、矛盾。
　よって、Ｍは、上に有界である。同様にして、Ｍは、下にも有界である。
Ｍの空でない任意の部分集合Ａは、上に有界であるから、上限 ａ を持つ。いま、ａ　がＡ に
属さないとすると、任意の自然数 ｎ に対して、ａ−1/n　は、Ａの上界でないから、
　　　　　　　　　　　　ａ−1/n　≦Ｘｎ＜ａ
となるＡの要素 Ｘｎ が存在する。このとき、Ｍの部分集合｛Ｘｎ｜ｎ≧１｝は最大数を持たない
ので、矛盾。よって、ａ は、Ａに属する。同様にして、下限 ｂ があって、ｂ　も Ａに属する。
　いま、Ｍが無限集合であると仮定する。
ａ₁ を、Ｍの上限とすると、 ａ₁　はＭに属する。さらに、Ｍ−｛ ａ₁｝の上限を、 ａ₂ とすると、
ａ₂　は、Ｍに属する。同様にして、数学的帰納法により、Ｍの点列　 ａ₁、ａ₂、・・・、ａ_ｎ、・・・
がとれる。ただし、ｎ≧２であれば、ａ_ｎ　は、Ｍ−｛ ａ₁、ａ₂・・・、ａ_n-1｝の上限である。
　このとき、Ｍの部分集合｛ａ_ｎ｜ｎ≧１｝は最小数を持たないので、矛盾。
したがって、Ｍは有限集合である。（終）

問題　３　（大阪大学）　の解答例（目次に戻る）

　R²上に、相異なる３点 Ａ、Ｂ、Ｃ をとる。
いま、ｆ は、１対１写像であるとすると、ｆ(Ａ)、ｆ(Ｂ)、ｆ(Ｃ) はすべて異なる。一般性を失うこと
なく、ｆ(Ａ)＜ｆ(Ｃ)＜ｆ(Ｂ) と仮定してよい。
　R²−{Ｃ} は弧状連結だから、連続写像 ξ ： ［０，１］→R²−{Ｃ} で、ξ(０)＝Ａ、ξ(１)＝Ｂ とな
るものが存在する。ξと ｆ は、連続写像だから、ｆ・ξ ： ［０，１］→R¹ は、連続写像で、しかも、
ｆ・ξ(０)＝ ｆ(Ａ)、ｆ・ξ(１)＝ ｆ(Ｂ) である。このとき、中間値の定理により、
ｆ・ξ(ｔ)＝ ｆ(Ｃ) となる ｔ (０＜ｔ＜１）が存在する。ξ(ｔ)＝Ｄとおくと、Ｃ≠Ｄ で、ｆ(Ｃ)＝f(D) となる。
これは、仮定に矛盾する。したがって、ｆ は、１対１写像でない。

問題　４　（大阪市立大学）　の解答例（目次に戻る）

　Ｘ＝Ｙ＝｛１，２，３，４｝とする。Ａ＝｛１，２｝、Ｂ＝｛３，４｝とおく。
いま、Ω_Ｘ＝｛Φ，Ａ，Ｂ，Ｘ｝、Ω_Ｙ＝｛Φ，Ｙ｝とおくと、Ω_Ｘ、Ω_Ｙは、Ｘ、Ｙの開集合系を定める。
このとき、（Ｘ、Ω_Ｘ）、（Ｙ、Ω_Ｙ）は位相空間となる。ただし、Ω_Ｘ⊃Ω_Ｙである。
　よって、ｆ を恒等写像とすると、ｆ は、ＸからＹの上への１対１連続写像となる。
しかるに、Ｘの開集合Ａに対して、ｆ^-1(Ａ)＝Ａ は、Ｙの開集合ではないので、ｆ^-1 は連続写像
となりえない。したがって、ｆ は同相写像ではない。

問題　５　（神戸大学）　の解答例（目次に戻る）

問１　集合Ｍが有限集合であると仮定する。（２）より、φは、ＭからＭへの写像で、また、
　　（３）より、φは、１対１の写像となり、上への写像になる。（１）から、０∈Ｍなので、
　　φ（Ｘ）＝０　となるＸ∈Ｍがある。これは、（４）に矛盾する。
　　　したがって、Ｍは無限集合である。
問２　Ｍとして、実数全体、φ（Ｘ）＝ｅ^-ｘ　とおくと、明らかに（１）〜（４）は成り立つが、（５）は
　　成り立たない。実際に、Ａ＝［０，１］　とおくと、０∈Ａ⊂Ｍ　かつ　φ（Ａ）⊂Ａ　であるが、
　　Ａ≠Ｍ　である。
問３　あるＸ∈Ｍに対して、φ（Ｘ）＝０　と仮定する。
　　Ａ＝｛Ｘ，φ（Ｘ），φ²（Ｘ），・・・｝、Ｂ＝｛φ（Ｘ），φ²（Ｘ），・・・｝とおくと、φ（Ｘ）＝０ だから、
　　０∈Ａ⊂Ｍ、０∈Ｂ⊂Ｍ　となる。また、φ（Ａ）⊂Ａ、φ（Ｂ）⊂Ｂ　である。
　　よって、（５）より、Ｍ＝Ａ＝Ｂ　が成り立つ。
　　　このとき、Ｘ∈Ｂ より、Ｘ＝φ^ｎ（Ｘ）となる自然数 ｎ が存在する。
　　よって、Ｍ＝｛Ｘ，φ（Ｘ），φ²（Ｘ），・・・φ^ｎ−1（Ｘ）｝となり、Ｍが無限集合であることに矛盾
　　する。したがって、Ｘ∈Ｍ　ならば、φ（Ｘ）≠０　である。
問４　Ｍ＝｛０，１｝とし、ｆ ：Ｍ→Ｍ　を、ｆ（０）＝１、ｆ（１）＝０　で定義する。
　　このとき、（１）（２）（３）（５）が成り立つが、（４）は成り立たない。

問題　６　（東北大学改題）　の解答例（目次に戻る）

　ψ(Ｘ＋Ｙ)＝ψ(Ｘ)ψ(Ｙ)　を満たすような実数全体を定義域とする実数値関数ψ(Ｘ)　を
任意にとる。
　（Ｘ＝０　での微分可能性を仮定すれば、このような関数は、ψ(Ｘ)＝Ｃｅ^ｘ　と定まるが、この場合は、
　　より一般的な場合を考えている。　→　参考「関数方程式」）
このとき、φ(Ｘ)＝ψ(Ｘ)＋ψ(−Ｘ)　とおくと、
　　φ(Ｘ＋Ｙ)＋φ(Ｘ−Ｙ)＝ψ(Ｘ＋Ｙ)＋ψ(−Ｘ−Ｙ)＋ψ(Ｘ−Ｙ)＋ψ(−Ｘ＋Ｙ)
　　　　　　　　　　　　　　　＝ψ(Ｘ)ψ(Ｙ)＋ψ(−Ｘ)ψ(−Ｙ)＋ψ(Ｘ)ψ(−Ｙ)＋ψ(−Ｘ)ψ(Ｙ)
　　　　　　　　　　　　　　　＝（ψ(Ｘ)＋ψ(−Ｘ))(ψ(Ｙ)＋ψ(−Ｙ)）
　　　　　　　　　　　　　　　＝φ(Ｘ)φ(Ｙ)
が成り立つので、φ(Ｘ)　は方程式を満たす。
　よって、方程式を満たす関数 φ(Ｘ) が一つ構成された。

（注）　広島工業大学の大川研究室より、次のようなご指摘をいただきました。そのご指摘を
　　　もとに、上記のように、解答（問題も！）を一部修正しました。

　　　　　　関数φ(Ｘ)　についての情報が曖昧である。
　　　　　（１）定義域は何処なのか？(実数全体と推測される？)
　　　　　　　値域も不明(これも実数全体と推測される？)
　　　　　（２）連続性は仮定するのかどうか？
　　　　　（３）その様な物を全部求めるのか、少なくとも１つ求めるのか？（少なくとも１つな
　　　　　　　ら、自明で、定数関数　たとえば、φ(Ｘ)＝２　がすぐ見つかる！）
　　　　　解答を見ると、　ψ(Ｘ＋Ｙ)＝ψ(Ｘ)ψ(Ｙ)　を満たす一般の関数 ψ(Ｘ) が書いてい
　　　　　ないので、結局の所は解の一例、φ(Ｘ) = e^x + e ^-x　を求めているのに過ぎない。
　　　　　他に、φ(Ｘ) = ２cos ( ax ) などいろいろある。

問題　７　（九州大学）　の解答例（目次に戻る）

　Ｅ を、Ｈａｕｓｄｏｒｆｆ 空間であるとする。任意の（Ｘ，Ｙ）∈ Ｅ×Ｅ−Δ とすると、Ｘ≠Ｙ だか
ら、 Ｘ∈Ｕ₁ 、Ｙ∈Ｕ₂ 、Ｕ₁∩Ｕ₂＝　である Ｅ の開集合 Ｕ₁ 、 Ｕ₂ が存在する。
　このとき、（Ｘ，Ｙ）∈Ｕ₁×Ｕ₂ ⊂Ｅ×Ｅ−Δ　が成り立つから、Ｅ×Ｅ−Δ は、Ｅ×Ｅ の
開集合である。よって、Δ は、Ｅ×Ｅ の閉集合である。逆も同様である。

問題　８　（京都大学）　の解答例（目次に戻る）

　Ａ と B は同相であるとすると、Ｓ＝｛（ｘ，ｙ）∈Ｒ²｜ｘ2＋ｙ2＝１｝ は、［ａ，ｂ］ に埋め込
める。即ち、Ｓ から Ｒ の中への同相写像 ｆ がある。　０≦θ≦２π に対して、
ｅ（θ）＝（ｃｏｓθ，ｓｉｎθ） とおくと、ｅ ：［０，２π］ → Ｓ は、連続な全単射である。
　特に、ｅ ：［０，２π） → Ｓ は連続な単射である。
よって、ｆ・ｅ ：［０，２π） → Ｒ は、連続な単射である。したがって、ｆ・ｅ は、［０，２π）で狭義
単調である。ｆ・ｅ は、［０，２π］で連続であるから、［０，２π］で狭義単調関数である。
［０，２π］ は連結ゆえ、ｆ・ｅ （［０，２π］） は区間である。ｆ・ｅ は単調だから、その区間は閉
区間で、ｆ・ｅ （０）、ｆ・ｅ （２π） は両端点である。ｅ （０）＝ｅ （２π） であるから、これは矛盾。
　したがって、Ａ と B とは同相になりえない。

問題　９　（立教大学）　の解答例（目次に戻る）

　Ａ、Ｂ がともに連結でないとすると、
　　　　　　　　　Ａ＝Ｆ∪Ｆ’　、Ｆ∩Ｆ’＝
　　　　　　　　　Ｂ＝Ｇ∪Ｇ’　、Ｇ∩Ｇ’＝
となるような、空でない閉集合 Ｆ、Ｆ’、Ｇ、Ｇ’ が存在する。
　このとき、次のように空でない閉集合 Ｈ、Ｈ’を定めることができる。
　　　Ａ∩Ｂ＝ のとき、
　　　　　Ｈ＝Ｆ∪Ｇ　、Ｈ’＝Ｆ’∪Ｇ’　とおく。
　　　Ａ∩Ｂ＝｛ ａ ｝ のとき、
　　　　　ａ∈Ｆ∩Ｇ としてよいから、Ｈ＝Ｆ∪Ｇ　、Ｈ’＝Ｆ’∪Ｇ’　とおく。
　　　Ａ∩Ｂ＝｛ ａ ，ｂ ｝ （ ａ ≠ ｂ ）のとき、ａ∈Ｆ∩Ｇ としてよい。
　　　　　ｂ∈Ｆ∩Ｇ　または　ｂ∈Ｆ’∩Ｇ’　のとき、Ｈ＝Ｆ∪Ｇ　、Ｈ’＝Ｆ’∪Ｇ’　とおく。
　　　　　ｂ∈Ｆ∩Ｇ’　のとき、Ｈ＝Ｆ∪Ｂ　、Ｈ’＝Ｆ’　とおく。
　　　　　ｂ∈Ｆ’∩Ｇ　のとき、Ｈ＝Ａ∪Ｇ　、Ｈ’＝Ｇ’　とおく。
このとき、Ａ∪Ｂ＝Ｈ∪Ｈ’　、Ｈ∩Ｈ’＝　となり、Ａ∪Ｂ が連結であることに矛盾する。
　よって、Ａ、Ｂ の少なくとも一方は連結である。

問題　１０　（名古屋大学）　の解答例（目次に戻る）

　行列 ^tＡ、Ａ^tＡ の表す線形写像をそれぞれ Ｆ、Ｇ とする。
任意の X∈ｋｅｒ Ｆ に対して、^tＡＸ＝Ｆ(Ｘ)＝Ｏ　より、Ｇ(Ｘ)＝Ａ^tＡＸ＝ＡＯ＝Ｏ
　よって、Ｘ∈ｋｅｒ Ｇ　が成り立つので、ｋｅｒ Ｆ ⊂ ｋｅｒ Ｇ
逆に、 任意の X∈ｋｅｒ Ｇ に対して、Ａ^tＡＸ＝Ｇ(Ｘ)＝Ｏ　より、^tＸＡ^tＡＸ＝Ｏ
　よって、｜^tＡＸ｜²＝（^tＡＸ，^tＡＸ）＝^tＸＡ^tＡＸ＝Ｏ　がいえるので、^tＡＸ＝Ｏ
したがって、X∈ｋｅｒ Ｆ　が成り立つので、ｋｅｒ Ｇ ⊂ ｋｅｒ Ｆ
　以上から、ｋｅｒ Ｆ ＝ ｋｅｒ Ｇ　が成り立つ。
このとき、
　ｒａｎｋ ^tＡ ＝ ｄｉｍ(ＩｍＦ) ＝ ｍ−ｄｉｍ(ｋｅｒ Ｆ) ＝ ｍ−ｄｉｍ(ｋｅｒ Ｇ) ＝ ｄｉｍ(ＩｍＧ)
ｄｉｍ(ＩｍＧ) ＝ ｒａｎｋ Ａ^tＡ だから、ｒａｎｋ ^tＡ ＝ ｒａｎｋ Ａ^tＡ　が成り立つ。
　ここで、ｒａｎｋ ^tＡ ＝ ｒａｎｋ Ａ なので、
　　　　　　　　　　　　ｒａｎｋ Ａ ＝ ｒａｎｋ Ａ^tＡ　
が成り立つ。

問題　１１　（東北大学）　の解答例（目次に戻る）

（１）　Ｆ（ｘ）＝ｄ（ｘ ，Ｂ）とおくと、Ｆは、Ａ上の連続関数である。Ａはコンパクト集合だから、
　　ある ａ∈Ａ が存在して、任意の ｘ ∈Ａ　に対して、ｄ（ａ ，Ｂ）≦ｄ（ｘ ，Ｂ）
　　　いま、ｄ（ａ ，Ｂ）＝０ とすると、Ｂは閉集合だから、ａ∈Ｂ となり、Ａ∩Ｂ＝ に矛盾
　　よって、任意の ｘ ∈Ａ　に対して、ｄ（ｘ ，Ｂ）＞０ より、ｄ（Ａ ，Ｂ）＞０
（２）　Ａ＝｛（ｘ ，ｙ）∈Ｒ²｜ｙ＝０ ｝、Ｂ＝｛（ｘ ，ｙ）∈Ｒ²｜ｘｙ＝１ ｝ とおくと、Ａ 、Ｂはともに
　　Ｒ² の閉集合で、Ａ∩Ｂ＝ である。しかるに、ｄ（Ａ ，Ｂ）＝０

問題　１２　（北海道大学）　の解答例（目次に戻る）

　題意より、Ｆ(Ｚ)＝ｕ(ｘ，ｙ)＋ｉｖ(ｘ，ｙ)　、Ｇ(Ｚ)＝ｅｘｐｕ(ｘ，ｙ)＋ｉｗ(ｘ，ｙ)　と書ける。ただし、
Ｚ＝ｘ＋ｉｙ とする。　Ｃａｕｃｈｙ-Ｒｉｅｍａｎｎの方程式より、
　　　　　　ｕ_ｘ＝ｖ_ｙ　、ｕ_ｙ＝−ｖ_ｘ　、ｅｘｐｕ・ｕ_ｘ＝ｗ_ｙ　、ｅｘｐｕ・ｕ_ｙ＝−ｗ_ｘ
が成り立つ。
　このとき、ｅｘｐｕ・ｕ_ｘ²＋ｅｘｐｕ・ｕ_ｘｘ＝ｗ_ｘｙ　、ｅｘｐｕ・ｕ_ｙ²＋ｅｘｐｕ・ｕ_ｙｙ＝−ｗ_ｘｙ　なので、

　　　　　　　　ｅｘｐｕ（ｕ_ｘ²＋ｕ_ｙ²）＋ｅｘｐｕ（ｕ_ｘｘ＋ｕ_ｙｙ）＝０

ｕ は調和関数なので、ｕ_ｘｘ＋ｕ_ｙｙ＝０　が成り立つ。　よって、ｅｘｐｕ（ｕ_ｘ²＋ｕ_ｙ²）＝０

ｅｘｐｕ≠０　より、ｕ_ｘ²＋ｕ_ｙ²＝０　なので、ｕ_ｘ ＝ｕ_ｙ ＝０　即ち、ｖ_ｘ ＝ｖ_ｙ ＝ｗ_ｘ ＝ｗ_ｙ ＝０

よって、ｕ、ｖ、ｗ は、定数となり、したがって、Ｆ(Ｚ)、Ｇ(Ｚ) は定数である。

問題　１３　（北海道大学）　の解答例（目次に戻る）

　ｍについての数学的帰納法により示す。
ｍ＝１　のとき、ｘ₁（ｇ）α₁＝０　において、ｘ₁（ｇ）≠０　より、α₁＝０　なので成り立つ。
いま、ｍ＞１　とし、ｍ より少ない個数の準同型に対して命題が成り立つとする。
　仮定より、　ｘ₁≠ｘ_m　なので、ｘ₁（ｈ）≠ｘ_m（ｈ）　となる ｈ∈Ｇ が存在する。
このとき、
　　　　　　ｘ₁（ｇ）ｘ₁（ｈ）α₁＋ｘ₂（ｇ）ｘ₂（ｈ）α₂＋・・・＋ｘ_m（ｇ）ｘ_m（ｈ）α_m＝０
　　　　　　ｘ₁（ｇ）ｘ_m（ｈ）α₁＋ｘ₂（ｇ）ｘ_m（ｈ）α₂＋・・・＋ｘ_m（ｇ）ｘ_m（ｈ）α_m＝０
辺々引いて、
　　　　ｘ₁（ｇ）（ｘ₁（ｈ）−ｘ_m（ｈ））α₁＋・・・＋ｘ_m-1（ｇ）（ｘ_m-1（ｈ）−ｘ_m（ｈ））α_m-1＝０
帰納法の仮定により、
　　　　　　（ｘ₁（ｈ）−ｘ_m（ｈ））α₁＝・・・＝（ｘ_m-1（ｈ）−ｘ_m（ｈ））α_m-1＝０
ここで、ｘ₁（ｈ）≠ｘ_m（ｈ）より、
　　　　　　　　　　　　　　　　　　　α₁＝０
よって、ｘ₂（ｇ）α₂＋・・・＋ｘ_m（ｇ）α_m＝０　から、α₂＝・・・＝α_m＝０　となり、命題は
ｍ についても成り立つ。
　以上から、数学的帰納法により、命題は、すべての自然数ｍについて成り立つ。

問題　１４　（大阪大学）　の解答例（目次に戻る）

　Ｖ が有限次元ベクトル空間のとき、　ｄｉｍ V ＝ｄｉｍ（ｋｅｒＦ）＋ｄｉｍＦ(Ｖ)　　が成り立つ。
このことより、Ｖ の一次変換 Ｆ が １対１であることと、Ｆ が上への一次変換であることと
は同値であることが分かる。
　Ｖ が無限次元空間のとき、このことは必ずしも成立しない。
Ｖ＝Ｃ［Ｘ］ とおくと、Ｖ はＣ上無限次元空間である。Ｆ： Ｖ → Ｖ を、Ｆ（ｆ(ｘ)）＝ ｆ’(ｘ) で
定義すると、Ｆ は Ｖ 上の一次変換である。このとき、Ｆ は全射であるが単射でない。
　実際に、ｋｅｒＦ ＝ Ｃ だからである。
次に、Ｆ： Ｖ → Ｖ を、Ｆ（ｆ(ｘ)）＝ ｘｆ(ｘ) で定義すると、Ｆ は Ｖ 上の一次変換である。
このとき、Ｆ は単射であるが全射でない。
　実際に、Ｃ （⊂Ｃ［Ｘ］）にうつる Ｃ［Ｘ］ の要素は存在しない。また、ｘｆ(ｘ) ＝ ０ とする
と、ｘ は多項式として ０ でないから、ｆ(ｘ) ＝ ０ となる。

問題　１５　（北海道大学）　の解答例（目次に戻る）

　Ｇ(Ｚ) ＝ Ｆ(Ｚ)−Ｆ(ａ) とおくと、Ｇ(Ｚ) は、| Ｚ−ａ | ＜１ で正則で、かつ、Ｇ(ａ) ＝ ０
このとき、Ｃａｕｃｈｙ の積分公式により、

　　　　　　　

となる。

問題　１６　（東京都立大学）　の解答例（目次に戻る）

　ｄｅｔ Ａ ＝１＋ａｄｅ＋ｂｃｆ−ａｃ−ｂｅ−ｄｆ　なので、
|ｄｅｔ Ａ|≧１−|ａｄｅ|−|ｂｃｆ|−|ａｃ|−|ｂｅ|−|ｄｆ|＞１−1/8−1/8−1/4−1/4−1/4＝０
　よって、ｄｅｔ Ａ ≠ ０　が成り立つ。

問題　１７　（名古屋大学）　の解答例（目次に戻る）

（１）　　ｄ（Ｐ，Ｆ(Ｐ)）≦ｄ（Ｐ，Ｑ）＋ｄ（Ｑ，Ｆ(Ｑ)）＋ｄ（Ｆ(Ｐ)，Ｆ(Ｑ)）
　　　　 ｄ（Ｑ，Ｆ(Ｑ)）≦ｄ（Ｐ，Ｑ）＋ｄ（Ｐ，Ｆ(Ｐ)）＋ｄ（Ｆ(Ｐ)，Ｆ(Ｑ)）　より、
　　　　　　|Ｇ(Ｐ)−Ｇ(Ｑ)|≦ｄ（Ｐ，Ｑ）＋ｄ（Ｆ(Ｐ)，Ｆ(Ｑ)）＜２ｄ（Ｐ，Ｑ）
　　が成り立つので、任意のε＞０　に対して、δ＝ε/２　とおけば、
　　　　　ｄ（Ｐ，Ｑ）＜δ　ならば、|Ｇ(Ｐ)−Ｇ(Ｑ)|＜２δ＝ε
　　であることが、任意のＰ、Ｑ∈Ｓ　に対して成り立つ。
　　　　よって、Ｇは、Ｓ上の連続関数である。
（２）　Ｓはコンパクトだから、最小値が存在する。すなわち、あるＰ∈Ｓ　が存在して、
　　全てのＱ∈Ｓ　に対して、Ｇ(Ｐ)≦Ｇ(Ｑ)　が成り立つ。
　　　いま、Ｐ≠Ｆ(Ｐ)　と仮定すると、
　　　　　　ｄ（Ｆ(Ｐ)，Ｆ(Ｆ(Ｐ))）＜ｄ（Ｐ，Ｆ(Ｐ)）　　すなわち、　Ｇ(Ｆ(Ｐ))＜Ｇ(Ｐ)
　　となり、Ｇ(Ｐ)が最小値であることに矛盾する。
　　　よって、　Ｆ(Ｐ)＝Ｐ　が成り立つ。
　　また、Ｐ≠Ｑ　となる　Ｐ、Ｑ∈Ｓ　で、Ｆ(Ｐ)＝Ｐ、Ｆ(Ｑ)＝Ｑ　が成り立つと仮定すると、
　　　　　　ｄ（Ｐ，Ｑ）＝ｄ（Ｆ(Ｐ)，Ｆ(Ｑ)）＜ｄ（Ｐ，Ｑ）
　　となり、矛盾である。
　　　よって、Ｆ(Ｐ)＝Ｐ を満たす点Ｐは唯一つである。

問題　１８　（奈良女子大学）　の解答例（目次に戻る）

　Ｆ(２Ｘ)＝Ｆ(Ｘ＋Ｘ)＝Ｆ(Ｘ)＋Ｆ(Ｘ)＝２Ｆ(Ｘ)、　Ｆ(３Ｘ)＝３Ｆ(Ｘ)、・・・　より、
自然数 ｎ に対して、Ｆ(ｎＸ)＝ｎＦ(Ｘ) が成り立つ。
　また、Ｆ(０)＝Ｆ(０)＋Ｆ(０)　より、Ｆ(０)＝０　で、Ｆ(０)＝Ｆ(Ｘ＋（−Ｘ）)＝Ｆ(Ｘ)＋Ｆ(−Ｘ)＝０
より、Ｆ(−Ｘ)＝−Ｆ(Ｘ)　が成り立つ。
このとき、自然数 ｎ に対して、Ｆ(（−ｎ）Ｘ)＝−Ｆ(ｎＸ)＝（−ｎ）Ｆ(Ｘ)　であるので、
整数 ｍ に対して、Ｆ(ｍＸ)＝ｍＦ(Ｘ) が成り立つ。
　また、自然数 ｎ に対して、
Ｆ(Ｘ)＝Ｆ(ｎ・（１/ｎ）Ｘ)＝ ｎ・Ｆ(（１/ｎ）Ｘ)　より、Ｆ(（１/ｎ）Ｘ)＝（１/ｎ）Ｆ(Ｘ)　が成り立つ。
　したがって、有理数 ｒ ＝ ｍ/ｎ （ｍ は整数、ｎ は自然数）に対して、
Ｆ(ｒＸ)＝Ｆ(（ｍ/ｎ）Ｘ)＝Ｆ(ｍ・（１/ｎ）Ｘ)＝ｍＦ(（１/ｎ）Ｘ)＝ｍ・（１/ｎ）Ｆ(Ｘ)＝（ｍ/ｎ）Ｆ(Ｘ)＝ｒＦ(Ｘ)
が成り立つ。
ここで、Ｆ(１)＝ａ とおくと、有理数 ｒ に対して、Ｆ(ｒ)＝ｒＦ(１)＝ａｒ　となる。
　任意の実数 Ｘ に対して、Ｘ に収束する有理数の点列｛ｒ_ｎ｝が存在する。
関数 Ｆ(Ｘ) は連続なので、任意の実数 Ｘ に対して、
　Ｆ(Ｘ)＝Ｆ(ｌｉｍ ｒ_ｎ)＝ｌｉｍ Ｆ(ｒ_ｎ)＝ｌｉｍ ａｒ_ｎ＝ａＸ　（ｌｉｍ はいずれも、ｎ→∞ とする。）
が成り立つ。（この問題に関連して、こちらを参照）

問題　１９　（大阪大学）　の解答例（目次に戻る）

　単位元を、ｅ とおくと、題意より、任意の ａ∈Ｇ に対して、ａ^ｎ＝ｅ が成り立つ。
いま、Ｇ₁＝｛ ａ∈Ｇ | ａ^ｎ₁＝ｅ ｝、Ｇ₂＝｛ ａ∈Ｇ | ａ^ｎ₂＝ｅ ｝　とおくと、Ｇ＝Ｇ₁×Ｇ₂ である。

Ｇ₁ の位数を ｍ₁、Ｇ₂ の位数を ｍ₂ とする。

ｎ＝ｍ₁・ｍ₂ だから、ｎ₁・ｎ₂＝ｍ₁・ｍ₂ である。

　いま、ｎ の任意の一つの素因数を、ｐ とし、任意の ａ∈Ｇ の位数を、ｄ とする。

ｄ が ｐ で割り切れる場合、ａ^d/p の位数は、ｐ である。

ｄ が ｐ で割り切れない場合、ａ によって生成される群を、Ｈ とおく。： Ｈ＝＜ａ＞
　このとき、商群 Ｇ/Ｈ の位数は、ｎ/ｄ で、ｎ よりも小さく、また、ｐ が素数であることから、
　ｎ/ｄ は ｐ で割り切れる。
　従って、群の位数に関する帰納法により、商群 Ｇ/Ｈ の元 ｂＨ で、位数が、ｐ であるもの
　が存在する。ｂ の位数を、ｋ とすると、（ｂＨ）^k ＝ ｂ^kＨ＝ｅＨ＝Ｈ　で、ｂＨ の位数は、ｐ で
　あるから、ｋ は、ｐ で割り切れる。このとき、ｂ^ｋ/p の位数は、ｐ である。

　以上により、位数 ｎ のアーベル群 Ｇ に対して、位数 ｎ の任意の素因数 ｐ を位数とする
ような ａ∈Ｇ が存在する。

　いま、ｍ₁ と ｎ₂ が互いに素でないとすると、ｍ₁ と ｎ₂ に共通な一つの素因数 ｐ がある。
この素因数 ｐ は、群 Ｇ₁ の位数 ｍ₁ の素因数なので、上記より、位数が ｐ の元 ｂ∈Ｇ₁
が存在する。このとき、ｎ₂ は、ｐ で割り切れるので、ｂ^ｎ₂＝ｅ である。よって、ｂ∈Ｇ₁∩Ｇ₂
であるから、ｂ＝ｅ となる。これは、矛盾である。
　よって、ｍ₁ と ｎ₂ は互いに素である。

同様にして、ｎ₁ と ｍ₂ も互いに素である。これより、ｎ₁・ｎ₂＝ｍ₁・ｍ₂ において、

　　　　　　ｎ₁ は、ｍ₁ で割り切れ、かつ、ｎ₂ は、ｍ₂ で割り切れる。
　　　　　　ｍ₁ は、ｎ₁ で割り切れ、かつ、ｍ₂ は、ｎ₂ で割り切れる。

　よって、ｎ₁ ＝ ｍ₁、ｎ₂ ＝ ｍ₂ となる。

　従って、 Ｇ₁ の位数は ｎ₁、Ｇ₂ の位数は ｎ₂ で、Ｇ₁ の定義より、位数 ｎ₁ の部分群は、
Ｇ₁ に限る。

問題　２０　（東北大学）　の解答例（目次に戻る）

（１）　帰納的に、ｄ（ｘ_ｎ+1，ｘ_ｎ）≦ａ^ｎ・ｄ（ｘ₁，ｘ₀） が成り立つ。
　　　三角不等式より、ｍ≧ｎ ならば、
　　　　ｄ（ｘ_ｍ，ｘ_ｎ）≦ｄ（ｘ_ｍ，ｘ_ｍ-1）＋・・・＋ｄ（ｘ_ｎ+1，ｘ_ｎ）≦（ａ^ｍ-1＋・・・＋ａ^ｎ）ｄ（ｘ₁，ｘ₀）
　　　すなわち、
　　　　　　　　　　　ｄ（ｘ_ｍ，ｘ_ｎ）≦ａ^ｎ（１−ａ^ｍ−ｎ）/（１−ａ）
　　　ここで、０＜ａ＜１ より、ｎ → ∞ のとき、ａ^ｎ → ０ なので、ｄ（ｘ_ｍ，ｘ_ｎ） → ０
　　　　したがって、点列｛ｘ_ｎ｝は、コーシー列である。
（２）　ｎ≧１ のとき、
　　　　　　　　　　　ｄ（Ｆ(ｘ*) ，ｘ*）≦ｄ（Ｆ(ｘ*)，Ｆ(ｘ_ｎ)）＋ｄ（Ｆ(ｘ_ｎ)，ｘ_ｎ）＋ｄ（ｘ_ｎ，ｘ*）
　　　　　　　　　　　　　　　　　　　　≦ａ・ｄ（ｘ*，ｘ_ｎ）＋ｄ（ｘ_ｎ+1，ｘ_ｎ）＋ｄ（ｘ_ｎ，ｘ*）
　　　ｎ → ∞ のとき、右辺の各項は、０ に収束するので、
　　　　　　　　　　　ｄ（Ｆ(ｘ*) ，ｘ*）＝０
　　　　よって、Ｆ(ｘ*) ＝ｘ* が成り立つ。
（３）　Ｆ(ｘ) ＝ｘ とする。ｄ（ｘ ，ｘ*）＝ｄ（Ｆ(ｘ)，Ｆ(ｘ*)）≦ａ・ｄ（ｘ，ｘ*）
　　　よって、　（１−ａ）ｄ（ｘ，ｘ*）≦０　より、ｄ（ｘ，ｘ*）＝０　が成り立つ。
　　　　したがって、ｘ ＝ｘ*

問題　２１　（）　の解答例

　　　以下工事中