「たすき掛け」は、「平方完成」などとならんで高校初年級でマスターしなければならない最
重要項目の一つであろう。ここで躓く者も多く、高校数学の一つの試金石と呼ぶに相応しい。
（注） 昔の家では着物を着ている人が多く、掃除などをするときに着物の袖が邪魔になるの
で、たすきを背中で斜め十文字に交差させ両肩に廻して結んでいた。後ろから見ると、
たすきが×になって見える。その方法を、たすき掛けと言う。（↓左下図参照）
合併した企業のトップ人事で交互にトップを交代する「たすき掛け」人事とか、世間でもよく
使われる。
「たすき掛け」も「平方完成」も２次方程式の解法に絡んでくる。「平方完成」という言葉は中
学では教わらないと思うが、その萌芽は教科書にも見られ、解の公式の理解に繋がっていく。
解の公式が使えれば「平方完成」から解放されると思いきや今度は２次関数の方でも呼び
出しがかかる。「平方完成」が中学から高校にかけてしばしば目にする機会が多いのに対し
て、「たすき掛け」自体は高校になってからの学びとなり、これがなかなか高校生に「たすき
掛け」が定着しない原因の一つと思われる。
「たすき掛け」は、２次式の因数分解の方策なわけであるが、中学の２次式の因数分解は
ｘ2＋ａｘ＋ｂ
のタイプに限定され、和がａ、積がｂとなる２数α、βを発見することにより、
ｘ2＋ａｘ＋ｂ＝（ｘ＋α）（ｘ＋β）
と因数分解される。これに対して、「たすき掛け」は、一般の２次式
ａｘ2＋ｂｘ＋ｃ
に有効な方法で、次のように考えるものである。
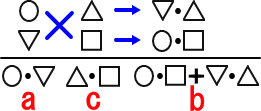
ａｘ2＋ｂｘ＋ｃ＝（○ｘ＋△）（▽ｘ＋□）
と因数分解されるとき、○、△、▽、□は次の式を満たす。
ａ＝○・▽ 、ｂ＝○・□＋▽・△ 、ｃ＝▽・□
この関係を満たす４数 ○、△、▽、□ を見つけるのに、次のような模式図で計算する方法
が、所謂、「たすき掛け」である。
例 ６ｘ2＋ｘ－２ を因数分解せよ。
（解） ａ＝６、ｂ＝１、ｃ＝－２ で、まず、ａ＝６ となる２数○、▽の可能性は、１と６、２と３
次に、ｃ＝－２ となる２数△、□の可能性は、「－」は保留しておいて、１と２
ここで、ｂ＝１ に注意して、「－」をどのように考慮しても○、▽が１と６では、ｂ＝１ は作
れないことに気がつく。
よって、○、▽は、２と３ で、△、□は、「－」は保留しておいて、１と２
あとは試行錯誤をして、次のようなたすき掛けで因数分解ができる。
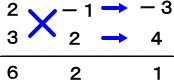
すなわち、 ６ｘ2＋ｘ－２＝（２ｘ－１）（３ｘ＋２） （終）
＃ ａの「２」と「３」は固定しておいて、後はｃが「１」と「２」なのか「２」と「１」なのかを「－」を絡
めながら考えると、たすき掛けのパターンは直ぐ見つけられるだろうし、経験を積めば、そ
れほど試行錯誤しなくてもいいようになるでしょう。
このように、中学までの和と差から２数を見つけるのに対して、「たすき掛け」の方法は試
行錯誤が入り若干込み入っていて、慣れないと難しく感じるかも知れない。中学校で学んだ
ことが活かせないというあたりが、「たすき掛け」が高校生に定着しない理由なのだと思われ
る。
中学では、ｘ2＋ａｘ＋ｂ の因数分解に限定され、高校で初めて一般の場合 ａｘ2＋ｂｘ＋ｃ
の因数分解が指導されるわけであるが、中学と高校に分断されているところが問題なのだ
ろう。中学でいっそのこと一般の場合の因数分解を「たすき掛け」で指導した方が定着度は
上がるのではないだろうか。
多分、中高一貫校ではそのような指導になっていることと推察される。
例 ｘ2＋５ｘ＋６ を因数分解せよ。
中学方式だと、和が５で積が６の２数は、２と３ なので、 ｘ2＋５ｘ＋６＝（ｘ＋２）（ｘ＋３）
であるが、たすき掛けを使っても次のようにできる。
（解） ａ＝１、ｂ＝５、ｃ＝６ で、まず、ａ＝１ となる２数○、▽は、１と１
次に、ｃ＝６ となる２数△、□の可能性は、「－」は保留しておいて、１と６ または ２と３
ここで、ｂ＝５ に注意して、△、□が１と６ または －１と－６ では、ｂ＝５ は作れない
ことに気がつく。
よって、○、▽は、１と１ で、△、□は、ｂ＝５＞０ から、２と３ と確定される。
以上から、次のようなたすき掛けで因数分解ができる。
すなわち、 ｘ2＋５ｘ＋６＝（ｘ＋２）（ｘ＋３） （終）
中学でも、このように因数分解を指導してくれれば、高校での因数分解の指導は軽減され
ることだろう。
ただ世の中には、どうしても「たすき掛け」は無理！という方もおられる。そのような方のた
めに、次のような「たすき掛け」回避策を伝授することにしている。
まず、ｘ2＋５ｘ＋６＝０ の解が、ｘ＝－２、－３ であることから、ｘ＋２＝０、ｘ＋３＝０ より
（ｘ＋２）（ｘ＋３）＝０ すなわち、 ｘ2＋５ｘ＋６＝（ｘ＋２）（ｘ＋３）
と因数分解されることを見せてから、いよいよ本題に入る。
６ｘ2＋ｘ－２＝０ の解を、解の公式を用いて、ｘ＝１/２、－２/３ であることから、
２ｘ－１＝０、３ｘ＋２＝０ より、 （２ｘ－１）（３ｘ＋２）＝０
よって、 ６ｘ2＋ｘ－２＝（２ｘ－１）（３ｘ＋２） と因数分解される。
たすき掛けの計算を多少軽減する方法として、西元教善先生の裏技が参考になると思う。
（→ 参考：「指導者のためのたすき掛け」）
また、算数おはじきセットのように、タイルを用いた「たすき掛け」の方法も知られている。
面積を用いる考え方で因数分解を捉えようとする方法である。
次の３種のタイルを用意する。面積は、それぞれ ｘ2、ｘ、１ である。
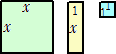
このタイルを用いて、次の因数分解の問題を解いてみよう。
（１） ｘ2＋６ｘ＋８
（２） ２ｘ2＋７ｘ＋６
（解）（１） 面積 ｘ2、ｘ、１ のタイルをそれぞれ １個、６個、８個用いて長方形を作ると、
よって、 ｘ2＋６ｘ＋８＝（ｘ＋４）（ｘ＋２） と因数分解される。
（２） 面積 ｘ2、ｘ、１ のタイルをそれぞれ ２個、７個、６個用いて長方形を作ると、
よって、 ２ｘ2＋７ｘ＋６＝（２ｘ＋３）（ｘ＋２） と因数分解される。
（コメント） このタイルによる「たすき掛け」の方法も、基本的には、面積１のタイルをどのよ
うな長方形にすればよいかを考えるところがポイントで、従来の「たすき掛け」の方法
と何ら変わるところはない。上記の問題 ２ｘ2＋７ｘ＋６ だと、「７」を「３」と「４」に分け
ればいいと気がつくことが重要で、これが出来る人は多分筆算でもたすき掛けができ
るだろうと思う。
上記では、係数が全て正の場合であったが、係数が負の場合も多少困難さを伴うが、タイ
ルを用いた「たすき掛け」は可能である。
例えば、６ｘ2－７ｘ－３ を因数分解してみよう。負の係数については、次のような負の面積
－ｘ、－１を持つタイルを別途用意する。
このとき、面積 ｘ2、－ｘ、－１ のタイルをそれぞれ ６個、７個、３個用いて長方形を作ろう
とすると作れないので、面積 －ｘ のタイルを２個増やし、面積 ｘ のタイルを２個追加するこ
とにより長方形を作ることができる。
よって、 ６ｘ2－７ｘ－３＝（２ｘ－３）（３ｘ＋１） と因数分解される。
（補足） まず、面積－１のタイルが３個なので、長方形を作るには横一列に並べるしかない。
さらに、面積 －ｘ のタイルが７個なので、３×３＝９ から、面積 －ｘ のタイルが９個必
要であることに気がつくので、面積 ｘ2 のタイル６個は上図のように配置される。後は
面積 ｘ のタイルを２個追加して長方形が完成する。
この場合、正の面積を持つタイルと同じ形状の負の面積を持つタイルが互いに接して併存
することはないことに注意する。
たすき掛けに代わる新しい因数分解の方法として、「取って掛け」という方法が知られてい
る。
（例） ６ｘ2－７ｘ－３ を因数分解する場合、ｘ2 の係数６を取って、定数校－３に掛けた２次式
ｘ2－７ｘ－１８
を考える。この因数分解は中学レベルの問題で、足して「－７」、掛けて「－１８」から、
ｘ2－７ｘ－１８＝（ｘ－９）（ｘ＋２）
と因数分解される。このことから、元の２次式 ６ｘ2－７ｘ－３ のｘ2 の係数６を「９」と「２」を割
り切るような２つの数 「３」と「２」に分解し、１次式の定数項を割り、割り算に使わなかった方
を１次式の ｘ の係数とする。
すなわち、 ６ｘ2－７ｘ－３＝（２ｘ－９/３）（３ｘ＋２/２）＝（２ｘ－３）（３ｘ＋１）
（コメント） 初めて見る解法で度肝を抜かれた気分！こんな解法があるんだと感動しました。
この原理を考えてみました。
ａｘ2＋ｂｘ＋ｃ＝（ｓｘ＋ｔ）（ｕｘ＋ｖ） と因数分解されたものとすると、 ａ＝ｓｕ である。
両辺をａ倍し、 （ａｘ）2＋ｂ（ａｘ）＋ａｃ＝ａ（ｓｘ＋ｔ）（ｕｘ＋ｖ）
ここで、 ａｘ＝Ｘ とおくと、 Ｘ2＋ｂＸ＋ａｃ＝ａ（ｓＸ/ａ＋ｔ）（ｕＸ/ａ＋ｖ）
＝ａ（Ｘ/ｕ＋ｔ）（Ｘ/ｓ＋ｖ）
＝（Ｘ＋ｕｔ）（Ｘ＋ｓｖ）
と書ける。このことから、
ａｘ2＋ｂｘ＋ｃ＝（Ｘ＋ｕｔ）（Ｘ＋ｓｖ）/ａ
＝（ａｘ＋ｕｔ）（ａｘ＋ｓｖ）/ａ＝（ｓｕｘ＋ｕｔ）（ｓｕｘ＋ｓｖ）/ｓｕ
＝（ｓｘ＋（ｕｔ）/ｕ）（ｕｘ＋（ｓｖ）/ｓ）＝（ｓｘ＋ｔ）（ｕｘ＋ｖ）
と因数分解される。
読者のために練習問題を残しておこう。
問題 ６ｘ2－１７ｘ＋１２ を因数分解せよ。
（解） ｘ2－１７ｘ＋７２＝（ｘ－９）（ｘ－８） より、 ６ｘ2－１７ｘ＋１２＝（２ｘ－３）（３ｘ－４）
問題 ３ｘ2＋１０ｘ－８ を因数分解せよ。
（解） ｘ2＋１０ｘ－２４＝（ｘ＋１２）（ｘ－２） より、 ３ｘ2＋１０ｘ－８＝（ｘ＋４）（３ｘ－２）
（コメント） この「取って掛け」という方法は、「たすき掛け」を苦手とする方の救世主となりえ
るだろうか．．．。
（追記） 令和２年１２月１３日付け
上記の「取って掛け」という方法は、因数分解のオーストラリア法と言われるらしい。
ａｘ2＋ｂｘ＋ｃ＝（ｓｘ＋ｔ）（ｕｘ＋ｖ） と因数分解されたものとすると、
ａ＝ｓｕ 、ｂ＝ｓｖ＋ｔｕ 、ｃ＝ｔｖ なので、 ａｃ＝（ｓｕ）×（ｔｖ）
これを、 ａｃ＝（ｓｖ）×（ｔｕ） の形に組み分けを変える点が肝要である。「取って掛け」と
いう方法では、最後の「１次式の定数項を割り、割り算に使わなかった方を１次式の ｘ の係
数とする」という処理が分かりづらいかもしれない。例を用いて、次のように計算するのがス
マートに思える。
例 ６ｘ2－１７ｘ＋１２ を因数分解せよ。
まず、ａｃ＝６×１２＝７２ で、ｂ＝－１７ から、 ａｃ＝（－８）×（－９） と分解できる。
このとき、
６ｘ2－１７ｘ＋１２＝（６ｘ－８）（６ｘ－９）/６＝（６ｘ－８）/２・（６ｘ－９）/３＝（３ｘ－４）（２ｘ－３）
問題 ４ｘ2－５ｘ－２１ を因数分解せよ。
（解） ａｃ＝４×（－２１）＝－８４ で、ｂ＝－５ から、 ａｃ＝（－１２）×７ と分解できる。
このとき、 ４ｘ2－５ｘ－２１＝（４ｘ－１２）（４ｘ＋７）/４＝（ｘ－３）（４ｘ＋７） （終）
（追記） 令和３年１月２８日付け
上記の「取って掛け」という方法を用いれば、ａｘ2＋ｂｘ＋ｃ のタイプの因数分解は、
ｘ2＋ａｘ＋ｂ のタイプの因数分解に還元される。
ここで、和が ａ 、積が ｂ となる２数が簡単に見つかればいいのだが、簡単に見つからな
い、そんな意地悪な問題がこの世には存在する。
例 ｘ2＋６４ｘ－１０９２ を因数分解せよ。
１０９２＝２×２×３×７×１３ で、いろいろ組合せを考えて、和が６４となる２数 －１４と７８
を見いだすことはそれほど易しいことではないだろう。
このような因数分解の問題に対して、次のような方法があることを最近知ることができた。
（因数分解の手順）
まず、ｘ の係数６４の半分を求める。： ６４/２＝３２
次に、この２乗を求める。： ３２2＝１０２４
次に、この１０２４から定数項－１０９２を引く。：１０２４－（－１０９２）＝２１１６
この２１１６の平方根を求める。：√２１１６＝４６
このとき、 ３２±４６を求める。： ３２±４６＝７８、－１４
この２数を用いて、次のように因数分解できる。： ｘ2＋６４ｘ－１０９２＝（ｘ＋７８）（ｘ－１４）
（コメント） 基本的には、ｘの係数が偶数のときの、解の公式利用の因数分解ですね！
（追記） 令和６年１１月１日付け
最近また、「取って掛け」という方法に触れる機会があった。「たすき掛け」に代わる方法と
して、世間の注目を集めているようだ。
求め方の原理は簡単である。
ａｃｘ2＋（ａｄ＋ｂｃ）ｘ＋ｂｄ＝（ａｘ＋ｂ）（ｃｘ＋ｄ） と因数分解されるが、
ａｃｘ2＋（ａｄ＋ｂｃ）ｘ＋ｂｄ を ｘ2＋（ａｄ＋ｂｃ）ｘ＋ｂｄ・ａｃ と書き換えてあげると、
ｘ2＋（ａｄ＋ｂｃ）ｘ＋ｂｄ・ａｃ＝（ｘ＋ａｄ）（ｘ＋ｂｃ）
と因数分解されることは明らかだろう。
そこで、 （ｘ＋ａｄ/ａｃ）（ｘ＋ｂｃ/ａｃ）＝（ｘ＋ｄ/ｃ）（ｘ＋ｂ/ａ） から、
（ｃｘ＋ｄ）（ａｘ＋ｂ） と書き直してあげると、因数分解は終了である。
例 ４ｘ2－５ｘ－２１ を因数分解せよ。
（解） ｘ2－５ｘ－２１・４＝（ｘ－１２）（ｘ＋７） において、
（ｘ－１２/４）（ｘ＋７/４）＝（ｘ－３）（ｘ＋７/４） から、因数分解は、
（ｘ－３）（４ｘ＋７） と完成する。 （終）
手順通りにやれば機械的に出来るかな？
例 ６ｘ2＋ｘ－２ を因数分解せよ。
（解） ｘ2＋ｘ－２・６＝（ｘ＋４）（ｘ－３） → （ｘ＋４/６）（ｘ－３/６）＝（ｘ＋２/３）（ｘ－１/２）
したがって、 ６ｘ2＋ｘ－２＝（３ｘ＋２）（２ｘ－１） と因数分解される。 （終）
以下工事中