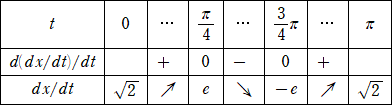嵟戝偲嵟彫丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂暯惉俀侽擭侾侾寧俆擔晅偗偱丄摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵丄俽乮俫乯偝傫偑丄師偺傛偆側
嵟戝嵟彫偺栤戣傪採埬偝傟偨丅
丂丂倶2亄倷2亖侾丂偑側傝偨偮偲偒丄乮倶亄倷乯4亄乮倶亅倷乯2丂偺嵟戝抣偲嵟彫抣傪媮傔傛丅
丂俽乮俫乯偝傫偐傜偺忣曬偵傛傟偽丄敾暿幃傪梡偄偨傝丄偦偺懠偵攠夘曄悢傪梡偄偨傝側偳偟
偰丄彮側偔偲傕俈捠傝偺夝朄偑懚嵼偡傞偲偄偆丅
丂俽乮俫乯偝傫偼丄弖帪偵俆屄偺夝朄傪巚偄偮偐傟偨偲偄偆丅巹傕丄偙偺栤戣偺暿夝偑偳傟傎
偳偁傞偺偐丄偳偺傛偆側暿夝偑壜擻側偺偐戝偄偵嫽枴偑偁偭偨偺偱丄偙偺儁乕僕偵偦傟傜
偺暿夝傪傑偲傔偨偄偲巚偆丅
暿夝偦偺侾丂丒丒丒丂堦斣嵟弶偵巚偄偮偄偨夝朄
丂倶亖們倧倱兤丄倷亖倱倝値兤丂偲偍偔偲丄
丂梌幃亖乮們倧倱兤亄倱倝値兤乯4亄乮們倧倱兤亅倱倝値兤乯2
丂亖乮侾亄倱倝値俀兤乯2亄侾亅倱倝値俀兤亖乮倱倝値俀兤乯2亄倱倝値俀兤亄俀亖乮倱倝値俀兤亄侾/俀乯2亄俈/係
亅侾亝倱倝値俀兤亝侾丂傛傝丄丂嵟戝抣偼丂係丄丂嵟彫抣偼丂俈/係
暿夝偦偺俀丂丒丒丒丂偪傚偭偲嫮堷偲傕巚偊傞夝朄乮夝朄偺巜恓偼暿夝偦偺侾偲傎偲傫偳摨偠乯
丂梌幃亖倶4亄係倶3倷亄俇倶2倷2亄係倶倷3亄倷4亄倶2亅俀倶倷亄倷2
丂亖乮侾亅倷2乯2亄係倶倷乮侾亅倷2乯亄俇乮侾亅倷2乯倷2亄係倶倷3亄倷4亄侾亅倷2亅俀倶倷亄倷2
丂亖亅係倷4亄係倷2亄俀倶倷亄俀亖係倷2乮侾亅倷2乯亄俀倶倷亄俀亖乮俀倶倷乯2亄俀倶倷亄俀
丂亖乮俀倶倷亄侾/俀乯2亄俈/係
偙偙偱丄憡壛暯嬒偲憡忔暯嬒偺娭學傛傝丄丂倶2亄倷2亞俀乥倶倷乥丂偱丄丂倶2亄倷2亖侾丂傛傝丄
丂侾亞俀乥倶倷乥丂偡側傢偪丄丂亅侾亝俀倶倷亝侾
偙偺偲偒丄丂嵟戝抣偼丂係丄丂嵟彫抣偼丂俈/係
乮曗懌乯丂忋婰偺寁嶼偱偼丄梌幃傪扨弮偵揥奐偟偨偑丄師偺傛偆偵寁嶼偟偰傕傛偄丅
丂倶2亄倷2亖侾丂傛傝丄丂乮倶亄倷乯2亅俀倶倷亖侾丂側偺偱丄丂乮倶亄倷乯2亖俀倶倷亄侾
傛偭偰丄
梌幃亖乮俀倶倷亄侾乯2亄倶2亅俀倶倷亄倷2亖乮俀倶倷亄侾乯2亅俀倶倷亄侾亖乮俀倶倷乯2亄俀倶倷亄俀
丂埲壓丄忋婰偲摨條偱偁傞丅
乮僐儊儞僩乯丂懅巕偵偙偺栤戣傪峫偊偰傕傜偭偨傜丄暿夝偦偺俀偺曗懌偺曽偱夝偄偰偄傑偟偨偹両
丂丂丂丂丂偙偪傜偺曽偑夝偒曽偲偟偰帺慠側偺偱偟傚偆偐丠偦偺侾偱夝偄偨巹偭偰丄傕偟偐偟偰曄
丂丂丂丂丂傢傝幰偐側丠
暿夝偦偺俁丂丒丒丒丂庴尡僥僋僯僢僋傪堄幆偟偨夝朄
丂倶亄倷亖倎丂丄倶倷亖倐丂偲偍偔偲丄倶丄倷
偼俀師曽掱幃丂倲2亅倎倲亄倐亖侽丂偺俀偮偺幚悢夝側偺偱丄
丂敾暿幃傪 俢
偲偍偔偲丄丂俢亖倎2亅係倐亞侽丂偑惉傝棫偮丅
丂偙偺偲偒丄丂倶2亄倷2亖乮倶亄倷乯2亅俀倶倷亖倎2亅俀倐亖侾丂側偺偱丄忋幃偵戙擖偟偰丄
丂倎2亅俀乮倎2亅侾乯亞侽丂偡側傢偪丄丂侽亝倎2亝俀丂偲側傞丅
傛偭偰丄
梌幃亖倎4亄倶2亄倷2亅俀倶倷亖倎4亅俀倐亄侾亖倎4亅乮倎2亅侾乯亄侾亖倎4亅倎2亄俀亖乮倎2亅侾/俀乯2亄俈/係
偙偺偲偒丄丂嵟戝抣偼丂係丄丂嵟彫抣偼丂俈/係
暿夝偦偺係丂丒丒丒丂偪傚偭偲攠夘曄悢偵嬅偭偨夝朄
丂倶亄倷亖俀倣丂丄倶亅倷亖俀値丂偲偍偔偲丄丂倶亖倣亄値丂丄丂倷亖倣亅値
偙偺偲偒丄丂倶2亄倷2亖侾丂傛傝丄丂乮倣亄値乯2亄乮倣亅値乯2亖侾丂側偺偱丄丂倣2亄値2亖侾/俀
丂値2亖侾/俀亅倣2亞侽丂側偺偱丄丂侽亝倣2亝侾/俀
傛偭偰丄
梌幃亖侾俇倣4亄係値2亖侾俇倣4亄係乮侾/俀亅倣2乯亖侾俇倣4亅係倣2亄俀亖侾俇乮倣2亅侾/俉乯2亄俈/係
偙偺偲偒丄丂嵟戝抣偼丂係丄丂嵟彫抣偼丂俈/係
暿夝偦偺俆丂丒丒丒丂暿夝偦偺係偺夝朄傪暿側帇揰偱帋傒偨夝朄
丂倶亄倷亖俀倣丂丄倶亅倷亖俀値丂偲偍偔偲丄丂倶亖倣亄値丂丄丂倷亖倣亅値
偙偺偲偒丄丂倶2亄倷2亖侾丂傛傝丄丂乮倣亄値乯2亄乮倣亅値乯2亖侾丂側偺偱丄丂倣2亄値2亖侾/俀
丂値2亖侾/俀亅倣2亞侽丂側偺偱丄丂侽亝倣2亝侾/俀丂偲側傞丅
偙偙偱丄丂梌幃亖侾俇倣4亄係値2丂偱偁傞偺偱丄丂倣2亖倃丂丄値2亖倄丂偲偍偔偲丄栤戣偼丄
丂倃亄倄亖侾/俀丂乮侽亝倃亝侾/俀乯丂偺偲偒丄丂侾俇倃2亄係倄丂偺嵟戝抣丄嵟彫抣傪栤偆傕偺偵東栿
偝傟傞丅
丂侾俇倃2亄係倄亖倠丂偲偍偒丄丂倄亖侾/俀亅倃丂傪戙擖偟偰惍棟偡傞偲丄侾俇倃2亅係倃亄俀亅倠亖侽
偲偄偆俀師曽掱幃偑摼傜傟傞丅偙偺俀師曽掱幃偑丄侽亝倃亝侾/俀丂偺斖埻偵偍偄偰丄彮側偔偲
傕堦偮夝偑偁傞傛偆偵丄掕悢
倠 偺抣偺斖埻傪掕傔傟偽傛偄丅
丂傑偢丄俀師娭悢丂俥乮倃乯亖侾俇倃2亅係倃亄俀亅倠丂偵偍偄偰丄
丂敾暿幃
俢/係亖係亅侾俇乮俀亅倠乯亖侾俇倠亅俀俉亞侽丂傛傝丄丂倠亞俈/係
丂傑偨丄幉偺幃偼丄丂倃亖侾/俉丂偱丄丂侽亝倃亝侾/俀丂偺斖埻撪偵偁傞丅
丂俥乮侾/俀乯亖係亅俀亄俀亅倠亖係亅倠亞侽丂傛傝丄丂倠亝係
丂埲忋偐傜丄丂俈/係亝倠亝係丂偲側傞偺偱丄丂嵟戝抣偼丂係丄丂嵟彫抣偼丂俈/係
暿夝偦偺俇丂丒丒丒丂俴倎倗倰倎値倗倕
偺枹掕忔悢朄傪棙梡偡傞夝朄
丂俧乮 倶 丆 倷 乯亖倶2亄倷2亅侾亖侽丂偺偲偒丄丂俥乮 倶 丆 倷 乯亖乮倶亄倷乯4亄乮倶亅倷乯2丂偺嬌抣傪媮傔
傞偙偲傪峫偊傞丅丂俴倎倗倰倎値倗倕 偺忔悢傪 兩
偲偡傞偲丄楢棫曽掱幃
丂俧乮 倶 丆 倷 乯亖侽丂丄俥倶乮 倶 丆 倷 乯亄兩俧倶乮 倶 丆 倷
乯亖侽丂丄俥倷乮 倶 丆 倷 乯亄兩俧倷乮 倶 丆 倷 乯亖侽
偺夝 乮 倶 丆 倷 乯偑丄嬌抣傪梌偊傞岓曗偲側傞丅
丂幚嵺偵丄丂係乮倶亄倷乯3亄俀乮倶亅倷乯亄俀兩倶亖侽丂丄丂係乮倶亄倷乯3亅俀乮倶亅倷乯亄俀兩倷亖侽
偐傜曈乆堷偔偲丄丂係乮倶亅倷乯亄俀兩乮倶亅倷乯亖侽丂傛傝丄丂俀乮倶亅倷乯乮兩亄俀乯亖侽丂偲側傞丅
丂倶亅倷亖侽丂偲偡傞偲丄丂倶亖倷亖 侾/
侾/ 丂偱偁傞丅
丂偱偁傞丅
丂偙偺偲偒丄丂俥乮 倶 丆 倷 乯亖乮倶亄倷乯4丂偺宍偐傜丄俥乮 倶 丆 倷 乯偼嬌戝偱丄
嬌戝抣丂俥乮 倶 丆 倷 乯亖係丂偲側傞丅
丂兩亖亅俀丂偲偡傞偲丄丂係乮倶亄倷乯3亄俀乮倶亅倷乯亅係倶亖侽丂偡側傢偪丄
丂係乮倶亄倷乯3亅俀乮倶亄倷乯亖侽丂偐傜丄丂俀乮倶亄倷乯乮俀乮倶亄倷乯2亅侾乯亖侽
傛偭偰丄丂倶亄倷亖侽丂丄侾/ 丂丄亅侾/
丂丄亅侾/ 丂偲側傞丅
丂偲側傞丅
丂倶亄倷亖侽丂偺偲偒丄丂倶亖 侾/
侾/ 丂丄倷亖
丂丄倷亖 侾/
侾/ 丂乮暋崋摨弴乯
丂乮暋崋摨弴乯
偙偺偲偒丄丂俥乮 倶 丆 倷 乯亖乮倶亅倷乯2丂偺宍偐傜丄俥乮 倶 丆 倷 乯偼嬌戝偱丄嬌戝抣丂俥乮 倶 丆 倷 乯亖俀
丂倶亄倷亖 侾/
侾/ 丂偺偲偒丄倶2亄倷2亖乮倶亄倷乯2亅俀倶倷亖侾/俀亅俀倶倷亖侾丂傛傝丄丂倶倷亖亅侾/係
丂偺偲偒丄倶2亄倷2亖乮倶亄倷乯2亅俀倶倷亖侾/俀亅俀倶倷亖侾丂傛傝丄丂倶倷亖亅侾/係
偙偺偲偒丄丂倶丂丄倷 偼丄俀師曽掱幃丂倲2 乮侾/
乮侾/ 乯倲亅侾/係亖侽丂偺俀偮偺夝側偺偱丄
乯倲亅侾/係亖侽丂偺俀偮偺夝側偺偱丄
丂倶亖乮
 亄
亄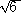 乯/係丂丄倷亖乮
乯/係丂丄倷亖乮
 亅
亅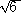 乯/係
乯/係
傑偨偼丄丂倶亖乮
 亅
亅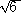 乯/係丂丄倷亖乮
乯/係丂丄倷亖乮
 亄
亄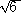 乯/係丂乮暋崋摨弴乯
乯/係丂乮暋崋摨弴乯
偙偺偲偒丄丂俥乮 倶 丆 倷 乯亖侾/係亄乮倶亅倷乯2丂偺宍偐傜丄俥乮 倶 丆 倷 乯偼嬌彫偱丄
嬌彫抣丂俥乮 倶 丆 倷 乯亖侾/係亄俁/俀亖俈/係丂偲側傞丅
丂埲忋偐傜丄嵟戝抣偼丂係丄嵟彫抣偼丂俈/係
暿夝偦偺俈丂丒丒丒丂僌儔僼昤夋偵傛傞夝朄乮僐儞僺儏乕僞棙梡乯
丂丂倶2亄倷2亖侾丂傛傝丄丂乮倶亄倷乯2亅俀倶倷亖侾丂側偺偱丄丂乮倶亄倷乯2亖俀倶倷亄侾
丂傛偭偰丄
梌幃亖乮俀倶倷亄侾乯2亄倶2亅俀倶倷亄倷2亖乮俀倶倷亄侾乯2亅俀倶倷亄侾亖係倶2倷2亄俀倶倷亄俀
偦偙偱丄丂 丂丂乮惵懢慄乯
丂丂乮惵懢慄乯
丂 丂丂乮愒懢慄乯
丂丂乮愒懢慄乯
偺僌儔僼傪丄僌儔僼昤夋僜僼僩傪梡偄偰昤偔偲丄壓恾偺傛偆偵側傞丅
丂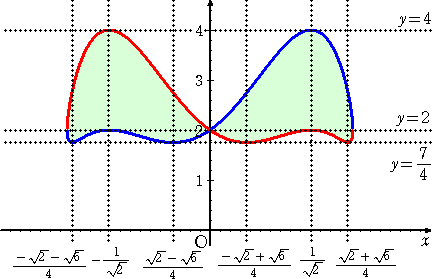
忋恾偐傜丄丂嵟戝抣偼丂係丄丂嵟彫抣偼丂俈/係
乮僐儊儞僩乯丂偙偺僌儔僼偐傜丄暿夝偦偺俇偺夦偟偐偭偨晹暘偑曗姰偝傟傑偡偹両
乮捛婰乯丂暯惉俀侾擭係寧俈擔晅偗
丂暯栰師榊丂挊丂乽夝朄偺敪尒乿丂乮妛惗幮乯丂偲偄偆彂愋傪壗偲偼側偟偵撉傫偱偄偨傜丄嵟
戝丒嵟彫偵偮偄偰丄怴偟偄帇嵗乮彮側偔偲傕巹偵偲偭偰丏丏丏両乯偲巚傢傟傞婰弎偵憳嬾偟偨丅
丂曄悢 倶 偺斖埻乮掕媊堟乯偑丄柦戣 俢乮倶乯 偵傛傝婯掕偝傟偰偄傞偲偒丄娭悢 倷亖俥乮倶乯
偺嵟彫抣 俵 傪媮傔傞偵偼丄柦戣 俢乮倶乯 偑恀偲側傞偁傞抣 倶亖倣 偵懳偟偰丄忢偵丄
丂忦審柦戣丂俢乮倶乯丂仺丂俥乮倶乯亅俥乮倣乯亞侽
偑惉傝棫偮偲偒偺 俵亖俥乮倣乯 偺抣傪掕傔傟偽傛偄丅
丂慡偔摨條偵丄嵟戝抣偵偮偄偰傕丄師偺傛偆偵懆偊傞偙偲偑弌棃傞丅
丂曄悢 倶 偺斖埻乮掕媊堟乯偑丄柦戣 俢乮倶乯 偵傛傝婯掕偝傟偰偄傞偲偒丄娭悢 倷亖俥乮倶乯
偺嵟戝抣 俶 傪媮傔傞偵偼丄柦戣 俢乮倶乯 偑恀偲側傞偁傞抣 倶亖値 偵懳偟偰丄忢偵丄
丂忦審柦戣丂俢乮倶乯丂仺丂俥乮倶乯亅俥乮値乯亞侽
偑惉傝棫偮偲偒偺 俶亖俥乮値乯 偺抣傪掕傔傟偽傛偄丅
丂偙傟傜偼丄嵟戝抣偲嵟彫抣偺掕媊偦偺傕偺偲尵偭偰傕夁尵偱偼側偔丄柍棟側偔椆夝偝傟傞
偙偲偲巚偆丅偙偺傛偆側帇揰偵棫偮偲丄掕媊堟偑暋嶨側応崌偵傕懳墳偱偒偦偆側丏丏丏梊姶両
丂偄偔偮偐嬶懱椺傪捠偟偰丄忋婰偺峫偊曽傪夛摼偡傞偙偲偵偟傛偆丅
椺丂倶 亞 侾 偺偲偒丄丂俥乮倶乯亖倶2亅係倶亄俁丂偺嵟彫抣傪媮傔傛丅
丂嫵壢彂摍偺傛偔抦傜傟偨夝朄偱偼丄師偺傛偆偱偁偭偨丅
乮夝乯丂俥乮倶乯亖倶2亅係倶亄俁亖乮倶亅俀乯2亅侾丂偱丄幉偺幃 倶亖俀 亞侾丂偐傜丄倶亖俀 偱嵟彫偱丄
丂嵟彫抣偼丄亅侾丂丂乮廔乯
丂偙偺栤戣傪怴偟偄帇嵗偱懆偊傞偲師偺傛偆偵側傞偱偁傠偆丅
乮夝乯丂柦戣丂倶 亞 侾丂偑恀偲側傞偁傞抣 倶亖倣丂傪峫偊傞偺偱丄倣亞侾丂偲偟偰傛偄丅
丂偙偺偲偒丄忦審柦戣丂倶 亞 侾丂仺丂俥乮倶乯亅俥乮倣乯亞侽丂偑惉傝棫偮傛偆偵丄倣 偺抣傪掕傔傟
偽傛偄丅偦偙偱丄俧乮倶乯亖俥乮倶乯亅俥乮倣乯丂偲偍偔偲丄俀師曽掱幃 俧乮倶乯亖侽丂偼丄倶亖倣丂傪夝偵
傕偮丅偡側傢偪丄丂倶2亅係倶亄俁亅俥乮倣乯亖侽丂偐傜丄敾暿幃傪俢偲偡傞偲丄
丂俢/係亖係亅乮俁亅俥乮倣乯乯亖俥乮倣乯亄侾亞侽丂傛傝丄丂俥乮倣乯亞亅侾
丂幚嵺偵丄俀師晄摍幃丂倶2亅係倶亄俁亅俥乮倣乯亞侽丂傪夝偄偰丄
丂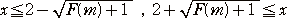
傛偭偰丄忦審柦戣丂倶 亞 侾丂仺丂俥乮倶乯亅俥乮倣乯亞侽丂偑忢偵惉傝棫偮偨傔偵偼
丂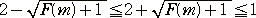
偱側偗傟偽側傜側偄丅乮仼丂偙偙偺晹暘偺寁嶼偱丄椞堟偺峫偊偑梡偄傜傟傞両乯
丂偲偙傠偱丄丂倶亖倣丂偼丄俀師曽掱幃 俧乮倶乯亖侽丂偺夝側偺偱丄
丂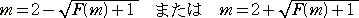
丂倣亞侾丂傛傝丄丂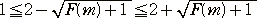
偟偨偑偭偰丄丂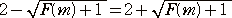 丂偑惉傝棫偮丅
丂偑惉傝棫偮丅
偙傟傪夝偄偰丄丂俥乮倣乯亖亅侾丂偱偁傞丅偙傟偑媮傔傞嵟彫抣偱偁傞丅
傑偨丄丂俥乮倣乯亖亅侾丂傛傝丄丂倣亖俀
丂埲忋偐傜丄丂倶亖俀丂偺偲偒丄丂嵟彫抣丂亅侾丂傪偲傞丅丂乮廔乯
乮僐儊儞僩乯丂偄偮傕偺夝摎偵斾傋丄戝曄偩偭偨偐側丠丂偙偺帇嵗偑妶桇偡傞偲偒傕偁傞偙偲傪
丂丂丂丂丂怣偠傞偙偲偵偟傛偆丏丏丏丅
椺丂倶2亅倶亅俀 亞 侽丂偺偲偒丄丂俥乮倶乯亖倶2亅俀倶亄俁丂偺嵟彫抣傪媮傔傛丅
丂嫵壢彂摍偺傛偔抦傜傟偨夝朄偱偼丄師偺傛偆偱偁偭偨丅
乮夝乯丂倶2亅倶亅俀 亞 侽丂偡側傢偪丄丂乮倶亅俀乯乮倶亄侾乯亞侽丂傛傝丄丂倶亝亅侾丄倶亞俀
丂丂俥乮倶乯亖倶2亅俀倶亄俁亖乮倶亅侾乯2亄俀丂傛傝丄倶亖俀 偱嵟彫偱丄嵟彫抣偼丄俁丂丂乮廔乯
丂偙偺栤戣傪怴偟偄帇嵗偱懆偊傞偲師偺傛偆偵側傞偱偁傠偆丅
乮夝乯丂柦戣丂倶2亅倶亅俀 亞 侽丂偡側傢偪丄丂倶亝亅侾丄倶亞俀丂偑恀偲側傞偁傞抣 倶亖倣丂傪峫
偊傞偺偱丄丂倣亝亅侾丄倣亞俀丂偲偟偰傛偄丅
偙偺偲偒丄忦審柦戣丂倶亝亅侾丄倶亞俀丂仺丂俥乮倶乯亅俥乮倣乯亞侽丂偑惉傝棫偮傛偆偵丄倣 偺抣傪
掕傔傟偽傛偄丅
丂偦偙偱丄俧乮倶乯亖俥乮倶乯亅俥乮倣乯丂偲偍偔偲丄俀師曽掱幃 俧乮倶乯亖侽丂偼丄倶亖倣丂傪夝偵傕偮丅
偡側傢偪丄丂倶2亅俀倶亄俁亅俥乮倣乯亖侽丂偐傜丄敾暿幃傪俢偲偡傞偲丄
丂俢/係亖侾亅乮俁亅俥乮倣乯乯亖俥乮倣乯亅俀亞侽丂傛傝丄丂俥乮倣乯亞俀
幚嵺偵丄俀師晄摍幃丂倶2亅俀倶亄俁亅俥乮倣乯亞侽丂傪夝偄偰丄
丂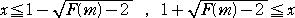
傛偭偰丄忦審柦戣丂倶亝亅侾丄倶亞俀丂仺丂俥乮倶乯亅俥乮倣乯亞侽丂偑忢偵惉傝棫偮偨傔偵偼
丂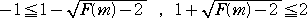
偱側偗傟偽側傜側偄丅
丂偲偙傠偱丄丂倶亖倣丂偼丄俀師曽掱幃 俧乮倶乯亖侽丂偺夝側偺偱丄
丂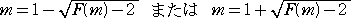
偱偁傞丅
偙偙偱丄丂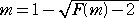 丂乮倣亙侾乯丂側傜偽丄倣亝亅侾丂傛傝丄
丂乮倣亙侾乯丂側傜偽丄倣亝亅侾丂傛傝丄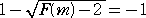
偱側偗傟偽側傜側偄丅偙傟傪夝偄偰丄 俥乮倣乯亖俇
丂傑偨丄丂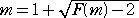 丂乮倣亜侾乯丂側傜偽丄丂倣亞俀丂傛傝丄
丂乮倣亜侾乯丂側傜偽丄丂倣亞俀丂傛傝丄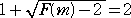
偱側偗傟偽側傜側偄丅偙傟傪夝偄偰丄 俥乮倣乯亖俁
丂俁亝俇丂側偺偱丄媮傔傞嵟彫抣偼丄丂俁丂偱偁傞丅
傑偨丄丂俥乮倣乯亖俁丂偱丄 倣亝亅侾丄倣亞俀丂偵拲堄偟偰丄丂倣亖俀
丂埲忋偐傜丄丂倶亖俀丂偺偲偒丄丂嵟彫抣丂俁丂傪偲傞丅丂乮廔乯
乮僐儊儞僩乯丂姷傟偰偔傞偲丄偩傫偩傫偼傑偭偰偄偒偦偆側夝朄偱偡偹両
丂暯惉俀侾擭俉寧俋擔晅偗偱丄俽乮俫乯偝傫傛傝師偺栤戣傪捀偄偨丅
乮梀傃怱偱捛壛偟偰偔偩偝偄丏丏丏偲偺偙偲側偺偱捛壛偟傑偟偨丒丒丒丂倖(^^;)丂乯
丂暯惉俀侽擭搙偺嶉嬍戝妛戝妛堾棟岺妛尋媶壢悢棟揹巕忣曬愱峌悢妛僐乕僗乮攷巑慜婜
壽掱乯偺擖帋栤戣傜偟偄偱偡丅
俼2 偱掕媊偝傟偨娭悢 俥乮 倶 丆 倷 乯亖 倶2倷丂丄俧乮 倶 丆 倷 乯亖 倶2亄倷4 傪峫偊傞丅
乮侾乯 俥倶亖兩俧倶丂丄俥倷亖兩俧倷丂丄俧乮 倶 丆 倷 乯亖侾丂傪枮偨偡幚悢偺慻 乮 倶 丆 倷 丆兩 乯
丂丂傪偡傋偰媮傔傛丅
乮俀乯 忦審 俧乮 倶 丆 倷 乯亖侾 偺壓偱丆娭悢 俥乮 倶 丆 倷 乯偺嵟戝抣偲嵟彫抣傪媮傔傛丅
丂乮侾乯偺梌偊曽偑丄Lagrange偺忔悢側偺偱丄偦偺夝朄偵廬偭偰夝偄偰偹両偲偄偆偙偲側偺偩
傠偆偑丄乮俀乯偩偗傪峫偊傟偽丄偦傫側嬄乆偟偔夝偐側偔偰傕丄悢妛嘨偺斖埻偱夝寛偱偒偦偆側
丏丏丏梊姶両
丂乮侾乯偵偮偄偰偼丄巜帵捠傝偵夝偔偟偐側偄偱偡傛偹両
乮夝乯丂忦審傛傝丄丂俀倶倷亖兩丒俀倶丂側偺偱丄丂倶亖侽丂傑偨偼丂倷亖兩
丂傑偨丄丂倶2亖兩丒係倷3丂丄丂倶2亄倷4亖侾丂偑惉傝棫偮丅
丂倶亖侽丂偺偲偒丄丂倷亖亇侾丂偱丄丂兩亖侽
丂倷亖兩丂偺偲偒丄丂侾亅兩4亖係兩4丂傛傝丄丂兩亖亇侾/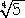 丂側偺偱丄丂倶亖亇俀/
丂側偺偱丄丂倶亖亇俀/
埲忋偐傜丄
乮 倶 丆 倷 丆兩 乯亖乮 侽 丆 侾 丆侽 乯丄乮 侽 丆 亅侾 丆侽 乯丄
丂丂乮 俀/ 丆 侾/
丆 侾/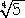 丆侾/
丆侾/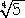 乯丄乮 俀/
乯丄乮 俀/ 丆 亅侾/
丆 亅侾/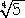 丆亅侾/
丆亅侾/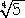 乯丄
乯丄
丂丂乮 亅俀/ 丆 侾/
丆 侾/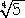 丆侾/
丆侾/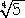 乯丄乮 亅俀/
乯丄乮 亅俀/ 丆 亅侾/
丆 亅侾/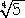 丆亅侾/
丆亅侾/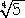 乯丄
乯丄
偺俇慻偁傞丅丂乮廔乯
丂乮俀乯偵偮偄偰偼丄師偺傛偆偵夝偔曽偑娙柧偩傠偆丅
乮夝乯丂倶2亄倷4亖侾丂傛傝丄丂倶2亖侾亅倷4亞侽丂側偺偱丄丂亅侾亝倷亝侾
偙偺偲偒丄丂倸亖倶2倷亖倷亅倷5丂乮亅侾亝倷亝侾乯丂偺嵟戝丒嵟彫傪媮傔傟偽傛偄丅
丂倸乫亖侾亅俆倷4亖侽丂偲偍偔偲丄丂倷亖亇侾/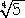
丂倸乭亖亅俀侽倷3丂傛傝丄
丂倷亖侾/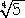 丂偺偲偒丄丂倸乭亙侽丂傛傝丄丂倸 偼嬌戝丂丂偙偺偲偒丄丂倶亖亇俀/
丂偺偲偒丄丂倸乭亙侽丂傛傝丄丂倸 偼嬌戝丂丂偙偺偲偒丄丂倶亖亇俀/
丂倷亖亅侾/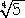 丂偺偲偒丄丂倸乭亜侽丂傛傝丄丂倸 偼嬌彫丂丂偙偺偲偒丄丂倶亖亇俀/
丂偺偲偒丄丂倸乭亜侽丂傛傝丄丂倸 偼嬌彫丂丂偙偺偲偒丄丂倶亖亇俀/
偲側傞丅僌儔僼傪昤偗偽丄壓恾偺傛偆偵側傞丅
丂丂丂丂丂丂丂丂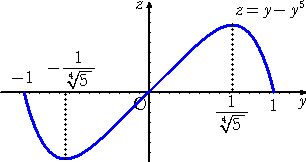
丂僌儔僼偐傜傕柧傜偐側傛偆偵丄
丂乮 倶 丆 倷 乯亖乮 俀/ 丆 侾/
丆 侾/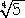 乯丄乮 亅俀/
乯丄乮 亅俀/ 丆 侾/
丆 侾/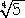 乯丂偺偲偒丄嵟戝偱丄
乯丂偺偲偒丄嵟戝偱丄
嵟戝抣偼丄丂係/乮俆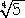 乯丂偱偁傞丅
乯丂偱偁傞丅
丂乮 倶 丆 倷 乯亖乮 俀/ 丆 亅侾/
丆 亅侾/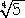 乯丄乮 亅俀/
乯丄乮 亅俀/ 丆 亅侾/
丆 亅侾/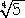 乯丂偺偲偒丄嵟彫偱丄
乯丂偺偲偒丄嵟彫偱丄
嵟彫抣偼丄丂亅係/乮俆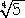 乯丂偱偁傞丅
乯丂偱偁傞丅
乮僐儊儞僩乯丂Lagrange 偺忔悢傪梡偄傞応崌偼丄倷 偺晞崋偐傜嵟戝丒嵟彫傪敾抐偡傞偺偐側丠
乮捛婰乯丂椷榓俇擭俋寧俇擔晅偗
丂戝妛擖帋偱偼丄嵟戝抣偲嵟彫抣傪媮傔傞栤戣偼昿弌偱偁傠偆丅
師偑搶杒戝妛丂棟宯乮侾俋俉侽乯偱弌戣偝傟偨丅
栤戣俀丂丂亅係亝倶亝侾 偺斖埻偱丄娭悢 俥乮倶乯亖佺倶倶+1 乥乮倲亄侾乯乮倲亄俀乯乥倓倲 偺嵟戝抣偲嵟
丂丂彫抣傪媮傔傛丅
乮夝乯丂倶亝亅俁丂偺偲偒丄
俥乮倶乯亖佺倶倶+1 乮倲亄侾乯乮倲亄俀乯倓倲亖佺倶倶+1 乷乮倲亄侾乯2亄乮倲亄侾乯乸倓倲
亖乵乮倲亄侾乯3/俁亄乮倲亄侾乯2/俀乶倶倶+1亖乷乮倶亄俀乯3亅乮倶亄侾乯3乸/俁亄乷乮倶亄俀乯2亅乮倶亄侾乯2乸/俀
偙偺偲偒丄俥乫乮倶乯亖乮倶亄俀乯2亅乮倶亄侾乯2亄乮倶亄俀乯亅乮倶亄侾乯亖俀乮倶亄俀乯亙侽
亅俁亝倶亝亅俀丂偺偲偒丄
俥乮倶乯亖佺倶-2 乷乮倲亄侾乯2亄乮倲亄侾乯乸倓倲亅佺-2倶+1 乷乮倲亄侾乯2亄乮倲亄侾乯乸倓倲
亖乵乮倲亄侾乯3/俁亄乮倲亄侾乯2/俀乶倶-2亅乵乮倲亄侾乯3/俁亄乮倲亄侾乯2/俀乶-2倶+1
亖侾/俁亅乷乷乮倶亄俀乯3亄乮倶亄侾乯3乸/俁亄乷乮倶亄俀乯2亄乮倶亄侾乯2乸/俀乸
偙偺偲偒丄俥乫乮倶乯亖亅俀乮倶亄俀乯2亝侽丂偱丄丂俥乫乮倶乯亖侽丂傛傝丄丂倶亖亅俀
亅俀亝倶亝亅侾丂偺偲偒丄
俥乮倶乯亖亅佺倶-1 乷乮倲亄侾乯2亄乮倲亄侾乯乸倓倲亄佺-1倶+1 乷乮倲亄侾乯2亄乮倲亄侾乯乸倓倲
亖亅乵乮倲亄侾乯3/俁亄乮倲亄侾乯2/俀乶倶-1亄乵乮倲亄侾乯3/俁亄乮倲亄侾乯2/俀乶-1倶+1
亖乷乮倶亄俀乯3亄乮倶亄侾乯3乸/俁亄乷乮倶亄俀乯2亄乮倶亄侾乯2乸/俀
偙偺偲偒丄俥乫乮倶乯亖俀乮倶亄俀乯2亞侽丂偱丄丂俥乫乮倶乯亖侽丂傛傝丄丂倶亖亅俀
倶亞亅侾丂偺偲偒丄
俥乮倶乯亖佺倶倶+1 乷乮倲亄侾乯2亄乮倲亄侾乯乸倓倲亖乵乮倲亄侾乯3/俁亄乮倲亄侾乯2/俀乶倶倶+1
亖乷乮倶亄俀乯3亅乮倶亄侾乯3乸/俁亄乷乮倶亄俀乯2亅乮倶亄侾乯2乸/俀
偙偺偲偒丄俥乫乮倶乯亖乮倶亄俀乯2亅乮倶亄侾乯2亄乮倶亄俀乯亅乮倶亄侾乯亖俀乮倶亄俀乯亜侽
埲忋偐傜丄倶亖亅俀丂偺偲偒丄俥乮倶乯偼嬌彫偐偮嵟彫偱丄嵟彫抣偼丄
丂俥乮亅俀乯亖亅侾/俁亄侾/俀亖侾/俇
偙偙偱丄俥乮亅係乯亖乮亅俉亄俀俈乯/俁亄乮係亅俋乯/俀亖俀俁/俇
丂俥乮侾乯亖乮俀俈亅俉乯/俁亄乮俋亅係乯/俀亖俆俁/俇
側偺偱丄倶亖侾丂偺偲偒丄俥乮倶乯偼嵟戝偱丄嵟戝抣偼丄丂俆俁/俇丂丂乮廔乯
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俇擭俋寧俉擔晅偗乯
丂|t亄1||t亄2| 偼楢懕娭悢側偺偱丄旝暘愊暘妛偺婎杮掕棟偑巊偊偰丄
丂F乫(x)亖|x亄2||x亄3| - |x亄1||x亄2|
偑偄偒側傝摼傜傟丄F乫(x)亖 0 側傜偽 x亖 -2 偲偡偖偵傢偐傝偦偆偱偡丅偳偆偱偟傚偆丠
乮僐儊儞僩乯丂DD++ 偝傫丄偛巜揈偁傝偑偲偆偛偞偄傑偡丅妋偐偵丄偦偆傗偭偰傕傛偐偭偨偱偡偹丅
丂|t亄侾||t亄俀| 偺尨巒娭悢傪 俧乮倲乯偲偍偔偲丄丂俧乫乮倲乯亖|t亄侾||t亄俀|丂偱偁傞丅
丂俥乮倶乯亖佺倶倶+1 |t亄侾||t亄俀|倓倲亖乵俧乮倲乯乶倶倶+1亖俧乮倶亄侾乯亅俧乮倶乯丂側偺偱丄
丂俥乫乮倶乯亖俧乫乮倶亄侾乯亅俧乫乮倶乯亖|倶亄俀||倶亄俁|亅|倶亄侾||倶亄俀|亖|倶亄俀|乮|倶亄俁|亅|倶亄侾|乯
傛偭偰丄丂倶亝亅俁丂偺偲偒丄丂俥乫乮倶乯亖俀乮倶亄俀乯亝侽
丂亅俁亝倶亝亅侾丂偺偲偒丄丂俥乫乮倶乯亖俀乮倶亄俀乯|倶亄俀|
丂倶亞亅侾丂偺偲偒丄丂俥乫乮倶乯亖俀乮倶亄俀乯亞侽
傛傝丄倶亖亅俀丂偺偲偒丄俥乮倶乯偼嬌彫偐偮嵟彫偱丄嵟彫抣偼丄侾/俇
傑偨丄倶亖侾丂偺偲偒丄俥乮倶乯偼嵟戝偱丄嵟戝抣偼丄丂俆俁/俇
乮捛婰乯丂椷榓俇擭俋寧俀俆擔晅偗
丂師偺栤戣偼丄旝暘朄偱偼偪傚偭偲壸偑廳偄偑丄恾宍揑偵峫偊傞偲斾妑揑梕堈偵夝偔偙偲偑
弌棃傞偙偲偵嬃偐偝傟傞丅
栤戣丂丂幚悢 倶 偵懳偟偰丄娭悢  偺嵟彫抣傪媮傔傛丅
偺嵟彫抣傪媮傔傛丅
乮夝乯丂 丂偲幃曄宍偡傞丅
丂偲幃曄宍偡傞丅
丂偙偺偲偒丄俹乮 倶 丆侽乯丄俙乮亅俀丆侾乯丄俛乮俀丆亅俀乯偲偍偔偲丄丂俥乮倶乯亖俙俹亄俛俹丂偲昞偝傟傞丅
傛偭偰丄俥乮倶乯偑嵟彫偲側傞偺偼丄俁揰俙丄俹丄俛偑堦捈慄忋偵偁傞偲偒偱偁傞丅
丂捈慄俙俛偺曽掱幃偼丄倷亖亅乮俁/係乯倶亅侾/俀丂偱丄倷亖侽丂偲偍偔偲丄倶亖亅俀/俁丂偐傜丄
俹乮亅俀/俁丆侽乯丂偺偲偒丄嵟彫偱丄嵟彫抣偼丄俆 偱偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俇擭俋寧俀俉擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉侾乯偺栤戣偼丄擖帋偺掕斣偲傕偄偊傞栤戣偱偁傞丅
栤戣俀丂丂暯柺忋偱晄摍幃 侽亝倷亝俀倶亝俇 偍傛傃 亅倶2亄係倶亅俁亝倷亝俀 傪摨帪偵枮偨偡椞
丂丂堟傪D偲偡傞丅
乮侾乯丂倎 偼 侽亝倎亝俀 偺斖埻偺掕悢偲偡傞丅偙偺偲偒丄晄摍幃 倎亝倶亝倎亄侾 傪枮偨偡椞堟偲D
丂偲偺嫟捠晹暘偺柺愊S(倎)傪媮傔傛丅
乮俀乯丂倎 偑 侽亝倎亝俀 偺斖埻傪摦偔偲偒丄S(倎)偺嵟戝抣偍傛傃嵟彫抣傪媮傔傛丅
乮夝乯乮侾乯丂侽亝倎亝侾丂偺偲偒丄
丂S(倎)亖佺a1 俀倶倓倶亄佺1a+1 (俀亅乮亅倶2亄係倶亅俁乯乯倓倶
丂亖佺a1 俀倶倓倶亄佺1a+1 (倶2亅係倶亄俆乯倓倶亖乮侾/俁乯倎3亅俀倎2亄俀倎亄侾
侾亝倎亝俀丂偺偲偒丄
丂S(倎)亖佺aa+1 (俀亅乮亅倶2亄係倶亅俁乯乯倓倶
丂亖佺aa+1 (倶2亅係倶亄俆乯倓倶亖倎2亅俁倎亄侾侽/俁
乮俀乯丂侽亝倎亝侾丂偺偲偒丄S乫(倎)亖倎2亅係倎亄俀亖侽丂偐傜丄丂倎亖俀亅 丂偱嬌戝偐偮嵟戝偱
丂偱嬌戝偐偮嵟戝偱
丂嵟戝抣偼丄丂乮係 亅侾乯/俁
亅侾乯/俁
丂倎亖侽丂偺偲偒丄丂S(侽)亖侾丂丄倎亖侾丂偺偲偒丄丂S(侾)亖係/俁
侾亝倎亝俀丂偺偲偒丄S(倎)亖倎2亅俁倎亄侾侽/俁亖乮倎亅俁/俀乯2亄侾俁/侾俀亞侾俁/侾俀亜侾
埲忋偐傜丄S(倎)偼丄倎亖俀亅 丂偺偲偒嵟戝偱嵟戝抣丂乮係
丂偺偲偒嵟戝偱嵟戝抣丂乮係 亅侾乯/俁
亅侾乯/俁
丂倎亖侽丂偺偲偒嵟彫偱丄嵟彫抣丂侾丂偱偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侽寧係擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉侾乯偺栤戣傕丄擖帋偺掕斣偲偄偊傞栤戣偱偁傞丅
栤戣丂丂嬫娫 侽亝倶亝侾 偵偍偄偰丄娭悢丂俥乮倶乯亖亅倶3亄俁倎倶丂乮倎 偼掕悢乯丂偺嵟戝抣偲嵟彫
丂丂抣傪媮傔傛丅
乮夝乯丂俥乫乮倶乯亖亅俁倶2亄俁倎亖亅俁乮倶2亅倎乯
倎亝侽丂偺偲偒丄俥乫乮倶乯亝侽丂偐傜丄俥乮倶乯偼扨挷偵尭彮偡傞丅
傛偭偰丄倶亖侽丂偺偲偒丄嵟戝偱丄嵟戝抣丂侽丂丄倶亖侾丂偺偲偒丄嵟彫偱丄嵟彫抣丂俁倎亅侾
侽亙倎亙侾丂偺偲偒丄倶亖併倎丂偺偲偒丄嬌戝偐偮嵟戝偱丄嵟戝抣丂俀倎併倎
丂偙偺偲偒丄俥乮侽乯亖侽丂丄俥乮侾乯亖俁倎亅侾丂偐傜丄
丂侽亙倎亝侾/俁丂偺偲偒丄丂嵟彫抣丂俁倎亅侾丂乮倶亖侾乯
丂倎亖侾/俁丂偺偲偒丄丂嵟彫抣丂侽丂乮倶亖侽丄侾乯
丂侾/俁亙倎亙侾丂偺偲偒丄丂嵟彫抣丂侽丂乮倶亖侽乯
倎亞侾丂偺偲偒丄嬫娫 侽亝倶亝侾 偵偍偄偰丄俥乫乮倶乯亞侽丂偐傜丄俥乮倶乯偼扨挷偵憹壛偡傞丅
傛偭偰丄倶亖侽丂偺偲偒嵟彫偱丄嵟彫抣丂侽丂丄倶亖侾丂偺偲偒嵟戝偱丄嵟戝抣丂俁倎亅侾丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾侾寧侾俋擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俇乯偺栤戣偼丄懍搙偑棈傓栤戣偱偁傞丅
栤戣俀丂丂悢捈慄忋偺俀偮偺摦揰俹丄俻偼帪崗侽偺偲偒尨揰偵偁傝丄帪崗 倲 偙偍偗傞丄偦傟偧
丂丂傟偺懍搙 倳(倲)丄倴乮倲乯 偼丄倳(倲)亖係倲2亅俇倎倲亅倎2丄倴(倲)亖倲2亄俇倎倲亅侾侽倎2丂偱偁傞丅偨偩偟丄
丂丂倎 偼幚悢偲偡傞丅
乮侾乯丂帪崗 倲 偵偍偗傞俀揰俹丄俻偺娫偺嫍棧 俥(倲) 傪媮傔傛丅
乮俀乯丂侽亝倲亝俁 偵偍偗傞 俥(倲) 偺嵟戝抣偲丄偦偺偲偒偺 倲 偺抣傪媮傔傛丅
乮俁乯丂乮俀乯偱媮傔偨嵟戝抣傪嵟傕彫偝偔偡傞 倎 偺抣傪媮傔傛丅
乮夝乯乮侾乯丂俹乮乮係/俁乯倲3亅俁倎倲2亅倎2倲乯丄俻乮乮侾/俁乯倲3亄俁倎倲2亅侾侽倎2倲乯丂傛傝丄
丂俥(倲) 亖乥倲3亅俇倎倲2亄俋倎2倲乥亖乥倲乥乮倲亅俁倎乯2
乮俀乯丂乮侾乯傛傝丄
 |
丂 |
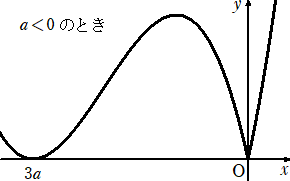 |
丂侽亝倲亝俁 偵偍偄偰丄俥(倲) 亖倲3亅俇倎倲2亄俋倎2倲丂傛傝丄
丂俥乫(倲) 亖俁倲2亅侾俀倎倲亄俋倎2亖俁乮倲亅倎乯乮倲亅俁倎乯
倎亜侽丂偺偲偒丄倶亖倎丂偱嬌戝丄倶亖俁倎丂偱嬌彫
丂俥(倎) 亖係倎3丂偱丄倲3亅俇倎倲2亄俋倎2倲亖係倎3丂偲偍偔偲偒丄乮倲亅倎乯2乮倲亅係倎乯亖侽
侽亙倎亝俁/係丂丄俁亝倎丂偺偲偒丄倶亖俁丂偺偲偒丄嵟戝抣丂俀俈乮倎亅侾乯2
俁/係亝倎亝俁丂偺偲偒丄倶亖倎丂偺偲偒丄嵟戝抣丂係倎3
倎亖侽丂偺偲偒丄俥(倲) 亖倲3丂偱丄侽亝倲亝俁 偵偍偄偰丄倶亖俁丂偺偲偒丄嵟戝抣 俀俈
倎亙侽丂偺偲偒丄倶亖俁丂偺偲偒丄嵟戝抣丂俀俈乮倎亅侾乯2
埲忋偐傜丄倎亝俁/係丄俁亝倎丂偺偲偒丄倶亖俁丂偺偲偒丄嵟戝抣丂俀俈乮倎亅侾乯2
丂俁/係亝倎亝俁丂偺偲偒丄倶亖倎丂偺偲偒丄嵟戝抣丂係倎3
乮俁乯丂乮俀乯偺僌儔僼偐傜丄
丂丂
丂傛偭偰丄媮傔傞 倎 偺抣偼丄丂倎亖俁/係丂丂乮廔乯
乮捛婰乯丂椷榓俇擭侾俀寧侾俆擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俉乯偺栤戣偼丄慺杙側挿曽宍偺柺愊偑棈傓栤戣偱偁傞丅
栤戣俀丂丂揰俷傪拞怱偲偡傞敿宎侾偺墌傪拞怱妏係兤乮侽亙兤亙兾/係乯偱愗偭偨偍偆偓宍偵丄
丂丂壓恾偺傛偆偵撪愙偡傞挿曽宍俙俛俠俢傪峫偊傞丅
丂丂
乮侾乯丂佢俙俷俛亖俀倶 偲偟偰丄挿曽宍俙俛俠俢偺柺愊 俽兤乮倶乯傪媮傔傛丅
乮俀乯丂俽兤乮倶乯傪嵟戝偵偡傞 倶 偺抣偲丄嵟戝抣俵乮兤乯傪媮傔傛丅
乮俁乯丂兤偑 侽亙兤亙兾/係 偺斖埻偱曄壔偡傞偲偒丄娭悢俵乮兤乯偺僌儔僼傪偐偗丅
乮夝乯乮侾乯丂俙俛亖俀倱倝値倶丂偱偁傞丅傑偨丄俙俢亖倛丂偲偍偔偲丄乮們倧倱倶亅倛乯倲倎値俀兤亖倱倝値倶丂傛傝丄
丂倛亖們倧倱倶亅倱倝値倶/倲倎値俀兤丂側偺偱丄挿曽宍俙俛俠俢偺柺愊偼丄
丂 俽兤乮倶乯亖俀倱倝値倶乮們倧倱倶亅倱倝値倶/倲倎値俀兤乯亖倱倝値俀倶亅俀倱倝値2倶/倲倎値俀兤
乮俀乯丂俽乫兤乮倶乯亖俀們倧倱俀倶亅係倱倝値倶們倧倱倶/倲倎値俀兤亖俀們倧倱俀倶亅俀倱倝値俀倶/倲倎値俀兤
丂亖乮俀倱倝値俀兤們倧倱俀倶-俀們倧倱俀兤倱倝値俀倶乯/倱倝値俀兤亖俀倱倝値乮俀兤-俀倶乯/倱倝値俀兤
丂侽亙兤亙兾/係丂偱丄侽亙倶亙俀兤丂傛傝丄丂侽亙俀兤亙兾/俀丂丄亅係兤亙亅俀倶亙侽丂側偺偱丄
丂亅係兤亙俀兤亅俀倶亙兾/俀丂偡側傢偪丄丂亅兾亙俀兤亅俀倶亙兾/俀
偙偺斖埻偱丄倱倝値乮俀兤-俀倶乯亖侽丂傪夝偔偲丄丂倶亖兤丂偱丄
丂侽亙倶亙兤丂偺偲偒丄丂倱倝値乮俀兤-俀倶乯亜侽丂偱丄兤亙倶亙俀兤丂偺偲偒丄丂倱倝値乮俀兤-俀倶乯亙侽
傛偭偰丄倶亖兤丂偺偲偒丄俽兤乮倶乯 偼嬌戝偐偮嵟戝偲側傞丅嵟戝抣偼丄
丂俵乮兤乯亖倱倝値俀兤亅俀倱倝値2兤/倲倎値俀兤亖倱倝値俀兤亅倱倝値兤們倧倱俀兤/們倧倱兤
丂亖倱倝値乮俀兤亅兤乯/們倧倱兤亖倱倝値兤/們倧倱兤亖倲倎値兤
乮俁乯丂媮傔傞僌儔僼偼壓恾丅
丂丂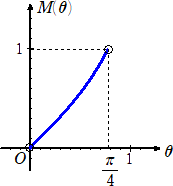 丂丂乮廔乯
丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾寧俈擔晅偗
丂師偺搶杒戝妛丂暥宯乮侾俋俉俉乯偺栤戣偼丄婎杮揑側椙栤偱偁傞丅
栤戣丂丂俁師娭悢俥乮倶乯偼丄倶亖侾 偱嬌彫抣侽丄倶亖亅俁 偱嬌戝抣俁俀傪偲傞丅
乮侾乯丂俥乮倶乯傪媮傔傛丅
乮俀乯丂揰俙(侽丆俥乮侽乯乯偵偍偗傞嬋慄 俠丗倷亖俥乮倶乯 偺愙慄俴偑傆偨偨傃俠偲岎傢傞揰傪俛偲偡傞丅
丂丂揰俹偑俠忋傪俙偐傜俛傑偱摦偔偲偒丄俹偲俴偲偺嫍棧偺嵟戝抣傪媮傔傛丅
乮夝乯乮侾乯丂戣堄傛傝丄丂俥乫乮倶乯亖倎乮倶亅侾乯乮倶亄俁乯亖倎乮倶2亄俀倶亅俁乯丂偲偍偗傞丅
丂偡側傢偪丄丂俥乮倶乯亖倎乮乮侾/俁乯倶3亄倶2亅俁倶乯亄倐
偙偺偲偒丄丂俥乮侾乯亖亅乮俆/俁乯倎亄倐亖侽丂丄俥乮亅俁乯亖俋倎亄倐亖俁俀
偙傟傪夝偄偰丄丂倎亖俁丂丄倐亖俆丂傛傝丄丂俥乮倶乯亖倶3亄俁倶2亅俋倶亄俆
乮俀乯丂揰俙(侽丆俆乯偵偍偗傞嬋慄 俠 偺愙慄俴偺曽掱幃偼丄丂倷亖亅俋倶亄俆
倶3亄俁倶2亅俋倶亄俆亖亅俋倶亄俆丂傛傝丄丂倶3亄俁倶2亖侽丂側偺偱丄俛乮亅俁丆俁俀乯
俹乮倲丆倲3亄俁倲2亅俋倲亄俆乯偲俴丗俋倶亄倷亅俆亖侽偲偺嫍棧倛偼丄丂倛亖乥倲3亄俁倲2乥/併俉俀
丂倷亖倲3亄俁倲2丂偲偍偔偲丄丂倷乫亖俁倲2亄俇倲亖俁倲乮倲亄俀乯亖侽丂傛傝丄丂倲亖侽丄亅俀
倷乭亖俇倲亄俇丂傛傝丄倲亖亅俀 偺偲偒丄倷乭亖亅俇亙侽 偐傜丄倷 偼丄倲亖亅俀 偺偲偒丄嬌戝偐偮嵟戝
偱嵟戝抣偼丄丂係丂偲側傞丅
丂偟偨偑偭偰丄俹偲俴偲偺嫍棧偺嵟戝抣偼丄丂係/併俉俀丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾寧侾俆擔晅偗
丂師偺搶杒戝妛丂棟宯乮侾俋俉俋乯偺栤戣偼丄傛偔峫偊傜傟偨椙栤偱偁傞丅
栤戣俆丂丂倎丄倐 傪 倎亞侾丄倎亗俀丄倐亜侽 側傞掕悢偲偟丄倶 偺娭悢 俥乮倶乯亖俀倕2x亅倎倕x亄倐倶 傪
丂丂峫偊傞丅
乮侾乯丂俥乮倶乯偑扨挷憹壛偲側傞偲偒丄倎丄倐 偺枮偨偡傋偒忦審傪媮傔傛丅
乮俀乯丂倷亖俥乮倶乯丄倷亖倐倶丄倶亖侽 偵傛傝埻傑傟傞恾宍偺柺愊俽傪媮傔傛丅
乮俁乯丂乮侾乯偺忦審偺傕偲偱丄倎 傪摦偐偡偲偒丄俽偺嵟戝抣俵傪倐偺娭悢偲偟偰昞偣丅
乮夝乯乮侾乯丂俥乫乮倶乯亖係倕2x亅倎倕x亄倐亞侽
倕x亖倲丂偲偍偔偲丄倲亜侽丂偵偍偄偰丄丂係倲2亅倎倲亄倐亞侽
倷亖係倲2亅倎倲亄倐丂偲偍偔偲丄丂倷亖係乮倲亅乮侾/俉乯倎乯2亄倐亅倎2/侾俇
倎亞侾丄倎亗俀丂側偺偱丄丂倷亞侽丂偱偁傞偨傔偺昁梫廫暘忦審偼丄丂倐亅倎2/侾俇亞侽
乮俀乯丂俥乮倶乯亖倐倶丂偲偍偔偲丄丂俀倕2x亅倎倕x亖侽
丂倕x亗侽丂側偺偱丄丂俀倕x亅倎亖侽丂懄偪丄丂倕x亖倎/俀丂傛傝丄丂倶亖倢倧倗乮倎/俀乯
倎亞侾丄倎亗俀丄俥乮侽乯亖俀亅倎丂偵拲堄偟偰丄
侾亝倎亙俀丂偺偲偒丄俥乮侽乯亖俀亅倎亜侽丂偱丄倶亖倢倧倗乮倎/俀乯亙侽
俥乮倶乯偼扨挷憹壛側偺偱丄
俽亖佺倢倧倗乮倎/俀乯0 乮俀倕2x亅倎倕x乯倓倶亖[倕2x亅倎倕x]倢倧倗乮倎/俀乯0亖倎2/係亅倎亄侾
倎亜俀丂偺偲偒丄俥乮侽乯亖俀亅倎亙侽丂偱丄倶亖倢倧倗乮倎/俀乯亜侽
俥乮倶乯偼扨挷憹壛側偺偱丄
俽亖佺0倢倧倗乮倎/俀乯 乮亅俀倕2x亄倎倕x乯倓倶亖[亅倕2x亄倎倕x]0倢倧倗乮倎/俀乯亖倎2/係亅倎亄侾
偟偨偑偭偰丄壗傟偵偟偰傕丂俽亖倎2/係亅倎亄侾丂偱偁傞丅
乮俁乯丂乮侾乯傛傝丄倐亅倎2/侾俇亞侽丂側偺偱丄丂亅係併倐亝倎亝係併倐丂懄偪丄
丂侾亝倎亝係併倐丂乮倎亗俀乯
偙偺斖埻偱丄俽亖倎2/係亅倎亄侾亖乮侾/係乯乮倎亅俀乯2丂偺嵟戝抣俵傪媮傔傞丅
侾亝係併倐亙俁丂懄偪丄丂侾/侾俇亝倐亙俋/侾俇丂偺偲偒丄倎亖侾丂偱嵟戝偱丄嵟戝抣俵亖侾/係
俁亝係併倐丂懄偪丄丂倐亞俋/侾俇丂偺偲偒丄倎亖係併倐丂偱嵟戝偱丄
丂嵟戝抣俵亖乮侾/係乯乮係併倐亅俀乯2亖乮俀併倐亅侾乯2丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俁寧俀俀擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋侽乯偺栤戣偼丄娭悢曽掱幃傪夝偔偺偑傑偢帋楙偱偁傞丅
栤戣丂丂娭悢俥乮倶乯偼旝暘壜擻偱丄偡傋偰偺 倶丄倷 偵懳偟偰丄師偺摍幃
丂丂俀俥乮乮倶亄倷乯/俀)亖俥乮倶乯亄 俥乮倷乯
傪枮偨偟偰偄傞偲偡傞丅
乮侾乯丂俥乮侽乯亖侽 偺偲偒丄俥乮倶乯傪媮傔傛丅
乮俀乯丂乮侾乯偱媮傔偨俥乮倶乯偺偆偪丄師偺愊暘丂佺02兾 乮俥乮倶乯亅倱倝値倶乯2倓倶丂偺抣傪嵟彫偵偡傞
丂丂俥乮倶乯傪媮傔傛丅
乮夝乯乮侾乯丂俀俥乮乮倶亄倷乯/俀)亖俥乮倶乯亄 俥乮倷乯丂偺椉曈傪 倷 傪屌掕偟偰 倶 偵偮偄偰旝暘偟偰丄
丂俥乫乮乮倶亄倷乯/俀)亖俥乫乮倶乯
偙偙偱丄丂倷亖亅倶丂偲偍偔偲丄俥乫乮倶乯亖俥乫乮侽乯丂偱偁傞丅偡側傢偪丄俥乫乮侽乯亖俠丂偲偍偔偲丄
丂俥乫乮倶乯亖俠丂偐傜丄丂俥乮倶乯亖俠倶亄俢丂乮俢偼掕悢乯丂偲彂偗傞丅俥乮侽乯亖侽 傛傝丄丂俢亖侽
埲忋偐傜丄丂俥乮倶乯亖俠倶丂乮俠偼掕悢乯丂偲側傞丅
乮俀乯丂佺02兾 乮俥乮倶乯亅倱倝値倶乯2倓倶亖佺02兾 乮俠倶亅倱倝値倶乯2倓倶
亖佺02兾 乮俠2倶2亅俀俠倶倱倝値倶亄倱倝値2倶乯倓倶
偙偙偱丄佺02兾 俠2倶2倓倶亖乮俉/俁乯俠2兾3
佺02兾 倶倱倝値倶倓倶亖[亅倶們倧倱倶乶02兾亄佺02兾 們倧倱倶倓倶亖亅俀兾亄[倱倝値倶乶02兾亖亅俀兾
佺02兾 倱倝値2倶倓倶亖乮侾/俀乯佺02兾 乮侾亅們倧倱俀倶乯倓倶亖乮侾/俀乯[倶亅乮侾/俀乯倱倝値倶乶02兾亖兾
側偺偱丄丂佺02兾 乮俥乮倶乯亅倱倝値倶乯2倓倶亖乮俉/俁乯俠2兾3亄係俠兾亄兾
丂倷亖乮俉/俁乯俠2兾3亄係俠兾亄兾丂偲偍偔偲丄丂倷乫亖乮侾俇/俁乯俠兾3亄係兾亖侽丂傛傝丄
丂俠亖亅俁/乮係兾2乯丂偺偲偒丄佺02兾 乮俥乮倶乯亅倱倝値倶乯2倓倶丂偼嵟彫偲側傞丅
丂偟偨偑偭偰丄丂俥乮倶乯亖亅乮俁/乮係兾2乯乯倶丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俁寧俀俇擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋侽乯偺栤戣偼丄柺愊偺寁嶼偑偟偭偐傝弌棃傞偐傪栤偆偰偄傞丅
栤戣丂丂倎 傪 侽亙倎亙侾 側傞悢偲偟丄俀偮偺曻暔慄 俠1丗倷亖亅俁倶2丄俠2丗倷亖俁倶2亅侾俉倎倶亄侾俀倎2
丂丂偵傛偭偰埻傑傟傞恾宍偺 倶亝侾 偺晹暘偺柺愊傪S偲偡傞丅
乮侾乯丂侽亙倎亝侾/俀 偺偲偒丄S傪倎偱昞偣丅
乮俀乯丂侾/俀亙倎亙侾 偺偲偒丄S傪倎偱昞偣丅
乮俁乯丂侽亙倎亙侾 偵偍偗傞S偺嵟戝抣偲丄偦偺偲偒偺倎傪媮傔傛丅
乮夝乯乮侾乯丂俁倶2亅侾俉倎倶亄侾俀倎2亖亅俁倶2丂偲偍偔偲丄倶2亅俁倎倶亄俀倎2亖乮倶亅倎乯乮倶亅俀倎乯亖侽
傛傝丄丂倶亖倎丄俀倎丂偱丄侽亙倎亝侾/俀 偺偲偒丄丂俀倎亝侾丂偱偁傞丅
俽亖佺a2a 乮亅俁倶2亅乮俁倶2亅侾俉倎倶亄侾俀倎2乯乯倓倶亖亅俇佺a2a 乮倶亅倎乯乮倶亅俀倎乯倓倶亖倎3
乮俀乯丂侾/俀亙倎亙侾 偺偲偒丄
俽亖佺a1 乮亅俁倶2亅乮俁倶2亅侾俉倎倶亄侾俀倎2乯乯倓倶亖亅俇佺a1 乮倶亅倎乯乮倶亅俀倎乯倓倶
丂亖俆倎3亅侾俀倎2亄俋倎亅俀
乮俁乯丂侽亙倎亝侾/俀 偺偲偒丄俽亖倎3丂傛傝丄俽乫亖俁倎2亜侽丂側偺偱丄俽偼扨挷偵憹壛偡傞丅
侾/俀亙倎亙侾 偺偲偒丄俽亖俆倎3亅侾俀倎2亄俋倎亅俀丂傛傝丄
丂俽乫亖侾俆倎2亅俀係倎亄俋亖俁乮俆倎2亅俉倎亄俁乯亖俁乮倎亅侾乯乮俆倎亅俁乯亖侽丂偐傜丄
丂倎亖侾丄俁/俆
丂傛偭偰丄俽偼丄倎亖俁/俆丂偺偲偒嬌戝偐偮嵟戝偱丄嵟戝抣偼丄係/俀俆丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俆寧俀侽擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俁乯偺栤戣偼丄乮俀乯偺嵟戝抣偺寁嶼偑挻僴乕僪両
栤戣丂丂曻暔慄俠丗倷亖亅乮侾/俀乯倶2亄係倶亅俇 傪峫偊傞丅揰(侽丆侾)傪捠傝丄孹偒偑 倲 偺捈慄傪俴
丂丂偲偡傞丅偨偩偟丄係亅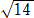 亝倲亝係亄
亝倲亝係亄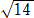 偲偡傞丅
偲偡傞丅
乮侾乯丂俠忋偺揰俹偵偍偗傞朄慄偑捈慄俴偲揰俻偱捈岎偡傞偲偒丄俹偲俻偺嵗昗傪媮傔傛丅
乮俀乯丂慄暘俹俻偺挿偝傪嵟戝偵偡傞 倲 偺抣傪媮傔傛丅
乮夝乯乮侾乯丂倷乫亖亅倶亄係亖倲丂傛傝丄丂倶亖係亅倲
偙偺偲偒丄丂倷亖亅乮侾/俀乯乮係亅倲乯2亄係乮係亅倲乯亅俇亖亅乮侾/俀乯倲2亄俀丂傛傝丄
丂俹乮係亅倲丆亅乮侾/俀乯倲2亄俀乯
揰俹偵偍偗傞朄慄偺曽掱幃偼丄
丂倷亖亅乮侾/倲乯乮倶亅係亄倲乯亅乮侾/俀乯倲2亄俀亖亅乮侾/倲乯倶亅乮侾/俀乯倲2亄係/倲亄侾
俴丗倷亖倲倶亄侾丂偲楢棫偟偰丄丂亅乮侾/倲乯倶亅乮侾/俀乯倲2亄係/倲亄侾亖倲倶亄侾丂偐傜丄
丂倶亖乮俉亅倲3乯/乮俀乮倲2亄侾乯乯
偙偺偲偒丄丂倷亖乮俉倲亅倲4乯/乮俀乮倲2亄侾乯乯亄侾丂傛傝丄
丂俻乮乮俉亅倲3乯/乮俀乮倲2亄侾乯乯丆乮俉倲亅倲4乯/乮俀乮倲2亄侾乯乯亄侾乯
乮俀乯丂俹俻2亖乮乮俉亅倲3乯/乮俀乮倲2亄侾乯乯亅係亄倲乯2亄乮乮俉倲亅倲4乯/乮俀乮倲2亄侾乯乯亄乮侾/俀乯倲2亅侾乯2
丂亖乮倲2亅俉倲亄俀乯2/乮係乮倲2亄侾乯乯
倷亖乮倲2亅俉倲亄俀乯2/乮係乮倲2亄侾乯乯丂偲偍偔偲丄
倷乫亖乮乮倲2亅俉倲亄俀乯乮俀倲亅俉乯乮倲2亄侾乯亅倲乮倲2亅俉倲亄俀乯2乯/乮俀乮倲2亄侾乯2乯
亖乮倲3亅俉乯乮倲2亅俉倲亄俀乯/乮俀乮倲2亄侾乯2乯亖乮倲亅俀乯乮倲2亄俀倲亄係乯乮倲2亅俉倲亄俀乯/乮俀乮倲2亄侾乯2乯
倷乫亖侽丂偲偍偔偲丄丂倲亖俀丄係亇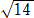 丂偱丄係亅
丂偱丄係亅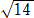 亙俀亙係亄
亙俀亙係亄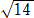
栤戣偺忦審丂係亅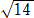 亝倲亝係亄
亝倲亝係亄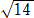 傛傝丄丂倲2亅俉倲亄俀亝侽丂偱丄倲2亄俀倲亄係亜侽丂偱偁傞丅
傛傝丄丂倲2亅俉倲亄俀亝侽丂偱丄倲2亄俀倲亄係亜侽丂偱偁傞丅
傛偭偰丄倷偼丄倲亖俀 偱丄嬌戝偐偮嵟戝偲側傞丅
埲忋偐傜丄慄暘俹俻偺挿偝傪嵟戝偵偡傞 倲 偺抣偼丄倲亖俀丂偲側傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俆寧俀俀擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋俁乯偺栤戣偼丄嶰妏宍偺柺愊偵娭偡傞栤戣偱偁傞丅
栤戣丂丂尨揰傪俷偲偟丄俀揰俙乮倰們倧倱兤丆倰倱倝値兤乯丄俛乮倱們倧倱乮兤亄兾/俀乯丆倱倱倝値乮兤亄兾/俀乯乯
丂丂偑懭墌 倶2/倎2亄倷2/倐2亖侾 乮倎亜侽丄倐亜侽乯偺忋偵偁傞偲偡傞丅偨偩偟丄倰亜侽丄倱亜侽 丅
乮侾乯丂仮俷俙俛偺柺愊俽傪 倎丄倐丄兤 偱昞偣丅
乮俀乯丂兤偑 侽亝兤亝兾 偺斖埻偱曄壔偡傞偲偒丄俽偺嵟戝抣偲嵟彫抣傪媮傔傛丅
乮夝乯乮侾乯丂俛乮亅倱倱倝値兤丆倱們倧倱兤乯丂偱偁傞偺偱丄
仮俷俙俛亖乮侾/俀乯乥倰倱們倧倱2兤亄倰倱倱倝値2兤乥亖倰倱/俀
戣堄傛傝丄丂倰2們倧倱2兤/倎2亄倰2倱倝値2兤/倐2亖侾丂偡側傢偪丄侾/倰2亖們倧倱2兤/倎2亄倱倝値2兤/倐2
傑偨丄倱2倱倝値2兤/倎2亄倱2們倧倱2兤/倐2亖侾丂偡側傢偪丄侾/倱2亖倱倝値2兤/倎2亄倱2們倧倱2兤/倐2
傛偭偰丄
侾/乮倰倱乯2亖乮們倧倱2兤/倎2亄倱倝値2兤/倐2乯乮倱倝値2兤/倎2亄們倧倱2兤/倐2乯
亖倱倝値2兤們倧倱2兤/倎4亄乮們倧倱4兤亄倱倝値4兤乯/(倎倐)2亄倱倝値2兤們倧倱2兤/倐4
亖倱倝値2俀兤/乮係倎4乯亄乮侾亅俀倱倝値2兤們倧倱2兤乯/(倎倐)2亄倱倝値2俀兤/乮係倐4乯
亖倱倝値2俀兤/乮係倎4乯亄乮侾亅乮侾/俀乯倱倝値2俀兤乯/(倎倐)2亄倱倝値2俀兤/乮係倐4乯
亖倱倝値2俀兤乮侾/乮係倎4乯亅侾/乮俀(倎倐)2乯亄侾/乮係倐4乯乯亄侾/(倎倐)2
傛傝丄
俽亖乮侾/俀乯丒併乮侾/乮倱倝値2俀兤乮侾/乮係倎4乯亅侾/乮俀(倎倐)2乯亄侾/乮係倐4乯乯亄侾/(倎倐)2乯乯
乮俀乯丂侽亝倱倝値2俀兤亝侾丂傛傝丄倱倝値2俀兤亖侽丂偡側傢偪丄兤亖侽丄兾/俀丄兾丂偺偲偒丄嵟戝偱丄
丂嵟戝抣丂倎倐/俀
倱倝値2俀兤亖侾丂偡側傢偪丄兤亖兾/係丄俁兾/係丂偺偲偒丄嵟彫偱丄
丂嵟彫抣丂乮侾/俀乯丒併乮侾/乮侾/乮係倎4乯亅侾/乮俀(倎倐)2乯亄侾/乮係倐4乯亄侾/(倎倐)2乯乯
亖乮侾/俀乯丒併乮侾/乮侾/乮係倎4乯亄侾/乮俀(倎倐)2乯亄侾/乮係倐4乯乯
亖併乮侾/乮侾/倎4亄俀/(倎倐)2亄侾/倐4乯乯亖侾/乮侾/倎2亄侾/倐2乯亖倎2倐2/乮倎2亄倐2乯丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俇寧係擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋係乯偺栤戣偼丄懍搙儀僋僩儖偵娭偡傞栤戣偱偁傞丅
栤戣丂丂倶倷暯柺偺尨揰傪俷偲偟丄捈慄俴丗倶亖侾丄嬋慄俠丗倷亖倶倢倧倗倶丂乮倶亜侽乯偲丄俴忋傪摦偔揰俹
丂丂傪峫偊傞丅帪崗 倲 (侽亝倲亝俀兾乯偺偲偒偺俹偺懍搙儀僋僩儖偼丄乮侽丆 們倧倱倲乯偱丄俹偼 倲亖侽
們倧倱倲乯偱丄俹偼 倲亖侽
丂丂偺偲偒丄揰乮侾丆侽乯偵偁傞丅捈慄俷俹偲俠偲偺岎揰傪俻偲偡傞丅偨偩偟丄懳悢偼帺慠懳悢偲偡
丂丂傞丅摦揰俻偺懍搙儀僋僩儖偺 倶 惉暘偑嵟戝丄嵟彫偲側傞帪崗偲丄偦偺偲偒偺俻偺嵗昗傪偦
丂丂傟偧傟媮傔傛丅
乮夝乯丂戣堄傛傝丄俹乮侾丆 倱倝値倲乯丂偲彂偗傞丅捈慄俷俹偺曽掱幃偼丄丂倷亖
倱倝値倲乯丂偲彂偗傞丅捈慄俷俹偺曽掱幃偼丄丂倷亖 倱倝値倲丒倶
倱倝値倲丒倶
丂倶倢倧倗倶亖 倱倝値倲丒倶丂偱丄倶亜侽丂傛傝丄丂倶亖倕丱乮
倱倝値倲丒倶丂偱丄倶亜侽丂傛傝丄丂倶亖倕丱乮 倱倝値倲乯丂偑揰俻偺 倶 嵗昗偲側傞丅
倱倝値倲乯丂偑揰俻偺 倶 嵗昗偲側傞丅
摦揰俻偺懍搙儀僋僩儖偺 倶 惉暘偼丄丂倓倶/倓倲亖 們倧倱倲丒倕丱乮
們倧倱倲丒倕丱乮 倱倝値倲乯
倱倝値倲乯
偙偺偲偒丄
倓乮倓倶/倓倲乯/倓倲亖亅 倱倝値倲丒倕丱乮
倱倝値倲丒倕丱乮 倱倝値倲乯亄俀們倧倱2倲丒倕丱乮
倱倝値倲乯亄俀們倧倱2倲丒倕丱乮 倱倝値倲乯
倱倝値倲乯
丂亖亅 乮
乮 倱倝値2倲亄倱倝値倲亅
倱倝値2倲亄倱倝値倲亅 乯倕丱乮
乯倕丱乮 倱倝値倲乯
倱倝値倲乯
丂亖亅 乮
乮 倱倝値倲亅侾乯乮倱倝値倲亄
倱倝値倲亅侾乯乮倱倝値倲亄 乯倕丱乮
乯倕丱乮 倱倝値倲乯亖侽丂偲偍偔偲丄丂倲亖兾/係丄俁兾/係
倱倝値倲乯亖侽丂偲偍偔偲丄丂倲亖兾/係丄俁兾/係
丂丂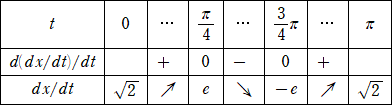
丂憹尭昞傛傝丄丂倲亖兾/係丂偺偲偒丄嵟戝偱丄倲亖俁兾/係丂偺偲偒丄嵟彫偲側傞丅
偦偺偲偒偺俻偺嵗昗偼丄壗傟傕丂乮倕丆倕乯丂偱偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俈寧俀俇擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮侾俋俋俈乯偺栤戣偼丄桿摫偑廏堩偱偁傞丅
栤戣丂丂乮侾乯丂摍幃 (侾亄倱倝値兤亄們倧倱兤乯2亖俀乮侾亄倱倝値兤乯乮侾亄們倧倱兤乯 偑惉傝棫偮偙偲傪
丂丂徹柧偣傛丅
乮俀乯丂兤偺娭悢 乮侾亄倱倝値兤乯乮侾亄們倧倱兤乯 偺 侽亱亝兤亙俁俇侽亱 偺斖埻偱偺嵟戝抣偍傛傃
丂丂嵟彫抣傪媮傔傛丅
乮夝乯乮侾乯丂(侾亄倱倝値兤亄們倧倱兤乯2
丂亖侾亄倱倝値2兤亄們倧倱2兤亄俀倱倝値兤亄俀倱倝値兤們倧倱兤亄俀們倧倱兤
丂亖俀乮侾亄倱倝値兤亄倱倝値兤們倧倱兤亄們倧倱兤乯亖俀乮侾亄倱倝値兤乯乮侾亄們倧倱兤乯
乮俀乯丂乮侾亄倱倝値兤乯乮侾亄們倧倱兤乯亖乮侾/俀乯(侾亄倱倝値兤亄們倧倱兤乯2
亖乮侾/俀乯(侾亄 倱倝値乮兤亄係俆亱乯乯2
倱倝値乮兤亄係俆亱乯乯2
侽亱亝兤亙俁俇侽亱 偺斖埻偱丄丂係俆亱亝兤亙俁俇侽亱亄係俆亱丂傛傝丄
亅 亝
亝 倱倝値乮兤亄係俆亱乯亝
倱倝値乮兤亄係俆亱乯亝 丂側偺偱丄丂侾亅
丂側偺偱丄丂侾亅 亝侾亄
亝侾亄 倱倝値乮兤亄係俆亱乯亝侾亄
倱倝値乮兤亄係俆亱乯亝侾亄
傛偭偰丄丂侽亝(侾亄 倱倝値乮兤亄係俆亱乯乯2亝俁亄俀
倱倝値乮兤亄係俆亱乯乯2亝俁亄俀 丂傛傝丄
丂傛傝丄
丂嵟戝抣丂乮俁亄俀 乯/俀丂乮兤亄係俆亱亖俋侽亱丂懄偪丄丂兤亖係俆亱丂偺偲偒乯
乯/俀丂乮兤亄係俆亱亖俋侽亱丂懄偪丄丂兤亖係俆亱丂偺偲偒乯
丂嵟彫抣丂侽
乮兤亄係俆亱亖俀俀俆亱丄俁侾俆亱丂懄偪丄丂兤亖侾俉侽亱丄俀俈侽亱丂偺偲偒乯丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俉寧俀擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮侾俋俋俉乯偺栤戣偼丄婎杮栤戣偩傠偆丅旝暘偟偰傕夝偗傞偑丄愨懳
抣傪巊偊偽梕堈偲側傞丅
栤戣丂丂兤偺娭悢 俥乮兤乯亖乮併乮侾亅們倧倱兤乯亄併乮侾亄倱倝値兤乯乯2 傪峫偊傞丅
乮侾乯丂倶亖們倧倱兤亄倱倝値兤 偲偍偔偲偒丄俥乮兤乯傪 倶 傪梡偄偰昞偣丅
乮俀乯丂俥乮兤乯偺嵟戝抣丄嵟彫抣傪媮傔傛丅
乮夝乯乮侾乯丂俥乮兤乯亖俀亅乮們倧倱兤亄倱倝値兤乯亄俀併乮侾亅乮們倧倱兤亄倱倝値兤乯亄倱倝値兤們倧倱兤乯
丂倶亖們倧倱兤亄倱倝値兤丂偲偍偔偲丄丂倱倝値兤們倧倱兤亖乮倶2亅侾乯/俀丂側偺偱丄
丂俥乮兤乯亖俀亅倶亄俀併乮侾亅倶亄乮倶2亅侾乯/俀乯亖俀亅倶亄併乮俀倶2亅係倶亄俀乯
丂亖俀亅倶亄 乥倶亅侾乥
乥倶亅侾乥
乮俀乯丂倶亖 倱倝値乮兤亄兾/係乯丂傛傝丄丂亅
倱倝値乮兤亄兾/係乯丂傛傝丄丂亅 亝倶亝
亝倶亝
傛偭偰丄亅 亝倶亝侾丂偺偲偒丄俥乮兤乯亖俀亅倶亅
亝倶亝侾丂偺偲偒丄俥乮兤乯亖俀亅倶亅 乮倶亅侾乯丂偐傜丄侾亝俥乮兤乯亝係亄俀
乮倶亅侾乯丂偐傜丄侾亝俥乮兤乯亝係亄俀
丂侾亝倶亝 丂偺偲偒丄俥乮兤乯亖俀亅倶亄
丂偺偲偒丄俥乮兤乯亖俀亅倶亄 乮倶亅侾乯丂偐傜丄侾亝俥乮兤乯亝係亅俀
乮倶亅侾乯丂偐傜丄侾亝俥乮兤乯亝係亅俀
埲忋偐傜丄丂嵟戝抣偼丄係亄俀 丂丄嵟彫抣偼丄侾丂丂乮廔乯
丂丄嵟彫抣偼丄侾丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俋寧俀俁擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋俋乯偺栤戣偼丄壗偲側偔夝偒偨偔側傞栤戣偱偁傞丅
栤戣丂丂俀偮偺妏兛丄兝乮侽亱亙兛丄兝亙俋侽亱乯偑丄倲倎値兛亄俀倲倎値兝亖俁 傪傒偨偡偲偡傞丅
乮侾乯丂俿亖侾/們倧倱2兛亄係/們倧倱2兝亄係們倧倱乮兛亅兝乯/乮們倧倱兛們倧倱兝乯偺抣傪媮傔傛.
乮俀乯丂俴亖侾/們倧倱兛亄俀/們倧倱兝偺嵟彫抣偲丄偦偺偲偒偺兛丄兝偺抣傪媮傔傛丅
乮夝乯乮侾乯丂俿亖侾亄倲倎値2兛亄係乮侾亄倲倎値2兝乯亄係乮侾亄倲倎値兛倲倎値兝乯
丂丂亖俋亄倲倎値2兛亄係倲倎値兛倲倎値兝亄係倲倎値2兝亖俋亄乮倲倎値兛亄俀倲倎値兝乯2亖侾俉
乮俀乯丂俴2亖乮侾/們倧倱兛亄俀/們倧倱兝乯亖侾/們倧倱2兛亄係/們倧倱2兝亄係/乮們倧倱兛們倧倱兝乯丂傛傝丄
丂俿亅俴2亖係乮們倧倱乮兛亅兝乯亅1乯/乮們倧倱兛們倧倱兝乯丂懄偪丄
丂俴2亖侾俉亄係乮侾亅們倧倱乮兛亅兝乯乯/乮們倧倱兛們倧倱兝乯丂偐傜丄俴偑嵟彫偲側傞偺偼丄
丂們倧倱乮兛亅兝乯亖侾丂偺偲偒偱丄嵟彫抣偼丄丂俁
偙偙偱丄丂侽亱亙兛丄兝亙俋侽亱丂傛傝丄丂亅俋侽亱亙兛亅兝亙俋侽亱丂側偺偱丄
丂兛亅兝亖侽丂懄偪丄丂兛亖兝丂偙偺偲偒丄倲倎値兛亖侾丂偐傜丄丂兛亖係俆亱
丂埲忋偐傜丄兛亖兝亖係俆亱丂偺偲偒丄俴偼嵟彫偱丄嵟彫抣丂俁 丂丂乮廔乯
丂丂乮廔乯
乮捛婰乯丂椷榓俈擭俋寧俀俈擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮俀侽侽侽乯偺栤戣偼丄俀師娭悢偺婎杮栤戣偩傠偆丅
栤戣丂丂兛丄兝偼丄|兛亄兝|亙俀傪枮偨偡暋慺悢偲偡傞丅偙偺偲偒丄娭悢
丂丂俥乮倶乯亖乮侾/係乯|兛亄兝|2倶2亅乮|兛|亄|兝|乯倶亄侾
偺侽亝倶亝侾偵偍偗傞嵟彫抣傪媮傔傛丅
乮夝乯丂|兛亄兝|亖侽丂偺偲偒丄俥乮倶乯偼 倶亖侾 偺偲偒嵟彫偱丄嵟彫抣偼丄亅乮|兛|亄|兝|乯亄侾
|兛亄兝|亗侽丂偺偲偒丄俥乮倶乯偼俀師娭悢偱丄幉偺曽掱幃偼丄倶亖俀乮|兛|亄|兝|乯/|兛亄兝|2
偙偙偱丄丂|兛亄兝|亙俀 傛傝丄俀/|兛亄兝|亜侾
傑偨丄丂|兛亄兝|亝|兛|亄|兝|丂傛傝丄丂|兛|亄|兝|/|兛亄兝|亞侾丂側偺偱丄
丂幉偺曽掱幃偼丄倶亖俀乮|兛|亄|兝|乯/|兛亄兝|2亜侾丂偱偁傞丅
傛偭偰丄俥乮倶乯偼 倶亖侾 偺偲偒嵟彫偱丄嵟彫抣偼丄乮侾/係乯|兛亄兝|2亅乮|兛|亄|兝|乯亄侾
丂偙傟偼丄|兛亄兝|亖侽丂偺応崌傕娷傓丅丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾侾寧俋擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮俀侽侽俀乯偺栤戣偼丄俀師娭悢偺婎杮栤戣偩傠偆丅
栤戣丂丂 侽亱亝兤亝侾俉侽亱偲偟偰丄倶 偺娭悢俥乮倶乯傪 俥乮倶乯亖倶2亄乮俀們倧倱兤/ 乯倶亅俀倱倝値兤
乯倶亅俀倱倝値兤
丂丂偲掕傔傞丅倶 偑惍悢傪摦偔偲偒偺俥乮倶乯偺嵟彫抣傪倣乮兤乯偲偍偔丅
乮侾乯丂兤偑 們倧倱兤亞 /俀 傪傒偨偡応崌偵丄倣乮兤乯偑嵟彫偲側傞兤偺抣傪媮傔傛丅
/俀 傪傒偨偡応崌偵丄倣乮兤乯偑嵟彫偲側傞兤偺抣傪媮傔傛丅
乮俀乯丂倣乮兤乯偑嵟彫偲側傞兤偺抣偲丄偦偺偲偒偺嵟彫抣傪媮傔傛丅
乮夝乯乮侾乯丂俥乮倶乯亖乮倶亄們倧倱兤/ 乯2亅乮侾/俁乯們倧倱2兤亅俀倱倝値兤
乯2亅乮侾/俁乯們倧倱2兤亅俀倱倝値兤
丂幉偺曽掱幃偼丄丂倶亖亅們倧倱兤/
丂們倧倱兤亞 /俀 偺偲偒丄丂侽亱亝兤亝俁侽亱偱偁傞丅偙偺偲偒丄亅們倧倱兤/
/俀 偺偲偒丄丂侽亱亝兤亝俁侽亱偱偁傞丅偙偺偲偒丄亅們倧倱兤/ 亝亅侾/俀
亝亅侾/俀
偐傜丄倶亖亅侾丂偺偲偒嵟彫偱丄嵟彫抣倣乮兤乯偼丄丂倣乮兤乯亖侾亅乮俀們倧倱兤/ 乯亅俀倱倝値兤
乯亅俀倱倝値兤
偙偺偲偒丄丂倣乮兤乯亖侾亅乮俀/ 乯乮
乯乮 倱倝値兤亄們倧倱兤乯亖侾亅乮係/
倱倝値兤亄們倧倱兤乯亖侾亅乮係/ 乯乮倱倝値乮兤亄俁侽亱乯
乯乮倱倝値乮兤亄俁侽亱乯
俁侽亱亝兤亄俁侽亱亝俇侽亱丂傛傝丄倣乮兤乯偼丄兤亄俁侽亱亖俇侽亱丂偡側傢偪丄兤亖俁侽亱丂偺
偲偒嵟彫偲側傞丅
乮俀乯丂乮侾乯丂傛傝丄丂們倧倱兤亞 /俀 傪傒偨偡応崌偵丄倣乮兤乯偼丄兤亖俁侽亱偺偲偒丄嵟彫偱丄
/俀 傪傒偨偡応崌偵丄倣乮兤乯偼丄兤亖俁侽亱偺偲偒丄嵟彫偱丄
丂嵟彫抣偼丄亅侾丂偱偁傞丅
丂亅 /俀亝們倧倱兤亝
/俀亝們倧倱兤亝 /俀丂偺偲偒丄丂俁侽亱亝兤亝侾俆侽亱
/俀丂偺偲偒丄丂俁侽亱亝兤亝侾俆侽亱
丂倶亖侽丂偺偲偒嵟彫偱丄嵟彫抣倣乮兤乯偼丄倣乮兤乯亖亅俀倱倝値兤
丂傛偭偰丄兤亖俋侽亱偺偲偒丄嵟彫偱丄嵟彫抣偼丄亅俀
丂們倧倱兤亝亅 /俀丂偺偲偒丄丂侾俆侽亱亝兤亝侾俉侽亱
/俀丂偺偲偒丄丂侾俆侽亱亝兤亝侾俉侽亱
丂倶亖侾丂偺偲偒嵟彫偱丄嵟彫抣倣乮兤乯偼丄
丂倣乮兤乯亖侾亄乮俀們倧倱兤/ 乯亅俀倱倝値兤亖侾亅乮係/
乯亅俀倱倝値兤亖侾亅乮係/ 乯乮倱倝値乮兤亅俁侽亱乯
乯乮倱倝値乮兤亅俁侽亱乯
丂侾俀侽亱亝兤亅俁侽亱亝侾俆侽亱丂傛傝丄倣乮兤乯偼丄兤亅俁侽亱亖侾俀侽亱偡側傢偪丄兤亖侾俆侽亱
偺偲偒嵟彫偱丄嵟彫抣偼丄亅侾丂偲側傞丅
丂埲忋偐傜丄兤亖俋侽亱偺偲偒丄倣乮兤乯偼嵟彫偲側傝丄嵟彫抣偼丄亅俀丂偱偁傞丅丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾侾寧侾侾擔晅偗
丂師偺搶杒戝妛丂慜婜暥宯乮俀侽侽俀乯偺栤戣傕丄婎杮揑側栤戣偩傠偆丅
栤戣丂丂 倲亞侾 偵偍偄偰丄娭悢 俥乮倲乯亖佺-11 |乮倶亅倲亄俀乯乮倶亄倲乯|倓倶 傪嵟彫偵偡傞 倲 偺抣偲丄
丂丂偦偺偲偒偺嵟彫抣傪媮傔傛丅
乮夝乯丂倲亞俁丂偺偲偒丄丂亅倲亝亅侾丂丄倲亅俀亞侾丂側偺偱丄
俥乮倲乯亖亅佺-11 乮倶亅倲亄俀乯乮倶亄倲乯倓倶 亖亅佺-11 乮倶2亄俀倶亄倲乮俀亅倲乯乯倓倶
丂亖亅乵倶3/俁亄倶2亄倲乮俀亅倲乯倶乶-11亖俀倲2亅係倲亅俀/俁
丂偙偺偲偒丄丂俥乫乮倲乯亖係倲亅係亜侽
侾亝倲亝俁丂偺偲偒丄丂亅倲亝亅侾丂丄倲亅俀亝侾丂側偺偱丄
俥乮倲乯亖亅佺-1t-2 乮倶亅倲亄俀乯乮倶亄倲乯倓倶亄佺t-21 乮倶亅倲亄俀乯乮倶亄倲乯倓倶
亖亅乵倶3/俁亄倶2亄倲乮俀亅倲乯倶乶-1t-2亄乵倶3/俁亄倶2亄倲乮俀亅倲乯倶乶t-21
亖乮係/俁乯倲3亅俇倲2亄俉倲亅俀/俁
丂偙偺偲偒丄丂俥乫乮倲乯亖係倲2亅侾俀倲亄俉亖係乮倲亅侾乯乮倲亅俀乯亖侽丂偲偍偔偲丄丂倲亖侾丄俀
丂倲亖侾丂偺偲偒丄嬌戝偱丄倲亖俀丂偺偲偒丄嬌彫偲側傞丅
傛偭偰丄娭悢 俥乮倲乯偑嵟彫偲側傞偺偼丄倲亖俀丂偺偲偒偱丄嵟彫抣偼丄俀丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾侾寧侾俀擔晅偗
丂師偺搶杒戝妛丂屻婜棟宯乮俀侽侽俀乯偺栤戣偼丄俀師娭悢偺婎杮栤戣偩傠偆丅
栤戣丂丂 倫亜侽 偲偡傞丅倶倷暯柺忋偺揰俙偑曻暔慄 倷2亖係倫倶 忋傪摦偔偲偒丄揰俙偲 倶 幉忋偺
丂丂揰乮倲丆侽乯偺嫍棧偺嵟彫抣俧乮倲乯傪媮傔傛丅偝傜偵丄倶亞侽 偺偲偒丄佺0x 俧乮倲乯倓倲 傪媮傔傛丅
乮夝乯丂揰俙乮倶丆倷乯丄倃乮倲丆侽乯丂偲偍偔偲丄
俙倃2亖乮倶亅倲乯2亄倷2亖乮倶亅倲乯2亄係倫倶亖乮倶亅倲亄俀倫乯2亄係倫倲亅係倫2
偙偺偲偒丄幉偺曽掱幃偼丄丂倶亖倲亅俀倫
倶亞侽 側偺偱丄丂倲亅俀倫亝侽丂傑偨偼丂倲亅俀倫亜侽丂偲応崌暘偗偟偰峫偊傞丅
丂倲亅俀倫亝侽丂偺偲偒丄丂倶亖侽丂偱嵟彫偱丄俙倃偺嵟彫抣偼丄乥倲乥
丂倲亅俀倫亜侽丂偺偲偒丄丂倶亖倲亅俀倫丂偱嵟彫偱丄俙倃偺嵟彫抣偼丄俀併乮倫倲亅倫2乯
埲忋偐傜丄丂倲亝俀倫丂偺偲偒丄丂俧乮倲乯亖乥倲乥
丂倲亜俀倫丂偺偲偒丄丂俧乮倲乯亖俀併乮倫倲亅倫2乯
丂侽亝倶亝俀倫 偺偲偒丄佺0x 俧乮倲乯倓倲亖佺0x 倲倓倲亖倶2/俀
丂俀倫亝倶丂偺偲偒丄
佺0x 俧乮倲乯倓倲亖佺0俀倫 俧乮倲乯倓倲亄佺俀倫x 俧乮倲乯倓倲
丂亖佺0俀倫 倲倓倲亄佺俀倫x 俀併乮倫倲亅倫2乯倓倲
丂亖俀倫2亄俀併倫佺俀倫x 併乮倲亅倫乯倓倲
丂亖俀倫2亄俀併倫乵乮俀/俁乯乮倲亅倫乯丱乮俁/俀乯乶俀倫x
丂亖乮係/俁乯併倫乷乮倶亅倫乯丱乮俁/俀乯亄乮俀/俁乯倫2丂丂乮廔乯
乮捛婰乯丂椷榓俈擭侾侾寧俀俀擔晅偗
丂師偺搶杒戝妛丂慜婜棟宯乮俀侽侽俁乯偺栤戣偼丄側偐側偐岻柇偵嶌傜傟偨栤戣偱偁傞丅
栤戣丂丂 俀偮偺娭悢傪丂倲亖們倧倱兤亄 倱倝値兤丂丄
倱倝値兤丂丄
丂丂倷亖亅係們倧倱俁兤亄們倧倱俀兤亅 倱倝値俀兤亄俀們倧倱兤亄俀
倱倝値俀兤亄俀們倧倱兤亄俀 倱倝値兤
倱倝値兤
偲偡傞丅
乮侾乯丂們倧倱俁兤傪 倲 偺娭悢偱昞偣丅
乮俀乯丂倷 傪 倲 偺娭悢偱昞偣丅
乮俁乯丂侽亱亝兤亝侾俉侽亱偺偲偒丄倷 偺嵟戝抣丄嵟彫抣偲偦偺偲偒偺兤偺抣傪媮傔傛丅
乮夝乯乮侾乯丂們倧倱俁兤亖係們倧倱3兤亅俁們倧倱兤亖們倧倱兤乮係們倧倱2兤亅俁乯
丂偙偙偱丄丂倲亅們倧倱兤亖 倱倝値兤丂偐傜丄
倱倝値兤丂偐傜丄
丂倲2亅俀倲們倧倱兤亄們倧倱2兤亖俁倱倝値2兤亖俁亅俁們倧倱2兤
傛偭偰丄丂係們倧倱2兤亅俁亖亅倲2亄俀倲們倧倱兤丂偲彂偗傞偺偱丄
丂們倧倱俁兤亖們倧倱兤乮亅倲2亄俀倲們倧倱兤乯亖亅倲2們倧倱兤亄俀倲們倧倱2兤
偙偙偱丄丂們倧倱2兤亖乮俁亅倲2亄俀倲們倧倱兤乯/係丂傪戙擖偟偰丄
丂們倧倱俁兤亖亅倲2們倧倱兤亄倲乮俁亅倲2亄俀倲們倧倱兤乯/俀亖倲乮俁亅倲2乯/俀
乮俀乯丂倷亖亅俀倲乮俁亅倲2乯亄們倧倱俀兤亅 倱倝値俀兤亄俀倲
倱倝値俀兤亄俀倲
偙偙偱丄丂們倧倱俀兤亅 倱倝値俀兤亖們倧倱2兤亅倱倝値2兤亅俀
倱倝値俀兤亖們倧倱2兤亅倱倝値2兤亅俀 倱倝値兤們倧倱兤
倱倝値兤們倧倱兤
偝傜偵丄倲2亖們倧倱2兤亄俀 倱倝値兤們倧倱兤亄俁倱倝値2兤丂傛傝丄
倱倝値兤們倧倱兤亄俁倱倝値2兤丂傛傝丄
丂俀 倱倝値兤們倧倱兤亖倲2亅們倧倱2兤亅俁倱倝値2兤
倱倝値兤們倧倱兤亖倲2亅們倧倱2兤亅俁倱倝値2兤
側偺偱丄們倧倱俀兤亅 倱倝値俀兤亖們倧倱2兤亅倱倝値2兤亅乮倲2亅們倧倱2兤亅俁倱倝値2兤乯亖俀亅倲2
倱倝値俀兤亖們倧倱2兤亅倱倝値2兤亅乮倲2亅們倧倱2兤亅俁倱倝値2兤乯亖俀亅倲2
傛偭偰丄丂倷亖亅俀倲乮俁亅倲2乯亄俀亅倲2亄俀倲亖俀倲3亅倲2亅係倲亄俀
乮俁乯丂倲亖俀倱倝値乮兤亄俁侽亱乯丂偱丄侽亱亝兤亝侾俉侽亱傛傝丄丂亅侾亝倲亝俀丂偱偁傞丅
丂倷乫亖俇倲2亅俀倲亅係亖俀乮倲亅侾乯乮俁倲亄俀乯亖侽丂偲偍偔偲丄丂倲亖侾丄亅俀/俁
傛偭偰丄憹尭昞偼丄
丂丂
偲側傞偺偱丄嵟戝抣偼丄俇丂乮倲亖俀丂偡側傢偪丄兤亖俇侽亱偺偲偒乯
丂嵟彫抣偼丄亅侾丂乮倲亖侾丂偡側傢偪丄兤亖侽亱丄侾俀侽亱偺偲偒乯丂丂乮廔乯
乮捛婰乯丂乮侾乯乮俀乯偵偮偄偰丄傕偭偲旤偟偄夝朄偑偁傝傑偟偨丅乮椷榓俈擭侾侾寧俀俈擔晅偗乯
乮暿夝乯乮侾乯丂倲亖們倧倱兤亄 倱倝値兤亖俀們倧倱乮兤亅兾/俁乯丂偲彂偗傞偺偱丄
倱倝値兤亖俀們倧倱乮兤亅兾/俁乯丂偲彂偗傞偺偱丄
丂們倧倱乮兤亅兾/俁乯亖倲/俀丂偱偁傞丅
偙偺偲偒丄丂們倧倱俁兤亖亅們倧倱乮俁兤亅兾乯亖亅們倧倱俁乮兤亅兾/俁乯
丂亖亅係們倧倱3乮兤亅兾/俁乯亄俁們倧倱乮兤亅兾/俁乯亖亅乮侾/俀乯倲3亄乮俁/俀乯倲亖倲乮俁亅倲2乯/俀
乮俀乯丂倷亖亅俀倲乮俁亅倲2乯亄們倧倱俀兤亅 倱倝値俀兤亄俀倲
倱倝値俀兤亄俀倲
丂偙偙偱丄們倧倱俀兤亅 倱倝値俀兤亖亅俀們倧倱乮俀兤亅俀兾/俁乯亖亅俀們倧倱俀乮兤亅兾/俁乯
倱倝値俀兤亖亅俀們倧倱乮俀兤亅俀兾/俁乯亖亅俀們倧倱俀乮兤亅兾/俁乯
丂亖亅係們倧倱2乮兤亅兾/俁乯亄俀亖亅倲2亄俀
側偺偱丄丂倷亖俀倲3亅倲2亅係倲亄俀丂偲彂偗傞丅丂丂乮暿夝廔乯
乮僐儊儞僩乯丂忋婰偺傛偆偵寁嶼偡傞偲丄僄儗僈儞僩偵媮傔傜傟傑偡偹両
丂丂埲壓丄岺帠拞







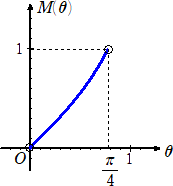 丂丂乮廔乯
丂丂乮廔乯