ヤングの定理 
当ＨＰの投稿において、「ある図形の性質」というものが考えられている。いろいろな方々
のお力添えで、
半径５/２の円内に互いの距離が２以上である点を９個配置することは不可能
であることが示された。
円と点の配置に関する定理として、ヤングの定理（Ｊ．Ｗ．Ｙｏｕｎｇ (1879〜1932)）が知ら
れている。
ヤングの定理
平面上に、ｎ 個の点が与えられている。ただし、どの２点間の距離も １
以下とする。
このとき、ｎ 個の点は全て、半径 
/３ の円の周および内部に存在する。
１辺の長さが１の正三角形の外接円の半径がちょうど、/３ であるので、「どの２点
間の距離も １ 以下」という束縛条件を満たす点は全て、この円の枠内に存在するという
ことである。
この定理を示すために、いくつか準備をしておこう。
補題Ａ 直線上に、ｎ 個の線分が与えられている。ただし、どの２つの線分も重なる部
分があるものとする。
このとき、全ての線分に共通する点が少なくとも一つ存在する。
（証明） 証明は、数学的帰納法による。
ｎ＝２ のとき、明らか
ｎ＝ｋ （ｋ≧２） のとき、成り立つと仮定する。
いま、ｋ＋１ 個の線分 Ｌ1、Ｌ2、・・・、Ｌｋ、Ｌｋ＋1 が直線上にあり、どの２つの線
分も重なる部分があるものとする。このとき、帰納法の仮定により、
ｋ 個の線分 Ｌ1、Ｌ2、・・・、Ｌｋ に対して、空ではない共通部分 Ｌ が存在する。
この Ｌ と Ｌｋ＋1 が重なることを示せば十分である。
いま、Ｌ と Ｌｋ＋1 が重ならないものと仮定する。このとき、Ｌ と Ｌｋ＋1 の間にある点
Ｐが存在する。ところが、ｋ 個の線分 Ｌ1、Ｌ2、・・・、Ｌｋ は、Ｌ と Ｌｋ＋1 の両方と重
なりを持つので、点Ｐは、ｋ 個の線分 Ｌ1、Ｌ2、・・・、Ｌｋ 全てに共通する点になる。
すなわち、Ｐは、Ｌに属する。これは、点Ｐが、Ｌに属さない点としたことに矛盾する。
よって、ｋ＋１ 個の線分 Ｌ1、Ｌ2、・・・、Ｌｋ、Ｌｋ＋1 に共通する点が存在する。
以上から、ｎ＝ｋ＋１ のときも成り立ち、２以上の全ての自然数に対して、命題は
成り立つ。（証終）
この補題Ａは、平面の場合に拡張される。
補題Ｂ 平面上に、ｎ 個の円板が与えられている。ただし、どの３つの円板も重なる部
分があるものとする。
このとき、全ての円板に共通する点が少なくとも一つ存在する。
（証明） 証明は、数学的帰納法による。
ｎ＝３ のとき、明らか
ｎ＝ｋ （ｋ≧３） のとき、成り立つと仮定する。
いま、ｋ＋１ 個の円板 Ｃ1、Ｃ2、・・・、Ｃｋ、Ｃｋ＋1 が平面上にあり、どの３つの円
板も重なる部分があるものとする。このとき、帰納法の仮定により、
ｋ 個の円板 Ｃ1、Ｃ2、・・・、Ｃｋ に対して、空ではない共通部分 Ｃ が存在する。
この Ｃ と Ｃｋ＋1 が重なることを示せば十分である。
いま、Ｃ と Ｃｋ＋1 が重ならないものと仮定する。Ｃｋ＋1 に最も近いＣ上の点をＡとす
る。このとき、左下図のように線分ＯＡに垂直な直線 Ｌ を考える。ＬがＣと交わるもの
 |
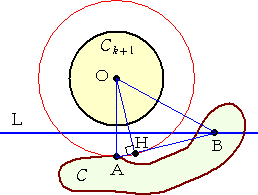とすると、∠ＯＡＢは鋭角で、ＯＡ≦ＯＢ より、
Ｈは線分ＡＢ上にあり、ＯＡ＞ＯＨ。
ところが、点Ａ、ＢはＣに属するので、ｋ 個の
円板 Ｃ1、Ｃ2、・・・、Ｃｋ に属する。このとき、
線分ＡＢは、ｋ 個の円板 Ｃ1、Ｃ2、・・・、Ｃｋ
に属することになり、点Ｈは、ｋ 個の円板
|
Ｃ1、Ｃ2、・・・、Ｃｋ すなわち、Ｃに属することになり、ＯＡ≦ＯＨ でなければならない。
これは矛盾である。 |
以上から、Ｃ と Ｃｋ＋1 の何れにも交わらない直線Ｌが存在することが分かった。
ところが、ｋ 個の円板 Ｃ1、Ｃ2、・・・、Ｃｋ は、Ｃ と Ｃｋ＋1 の両方と重なりを持つの
で、直線Ｌは、ｋ 個の円板 Ｃ1、Ｃ2、・・・、Ｃｋ 全てと交わる。直線Ｌの、ｋ 個の円
板 Ｃ1、Ｃ2、・・・、Ｃｋ との重なりの部分をそれぞれ Ｌ1、Ｌ2、・・・、Ｌｋ とする。
これらのどの２つをとっても重なる部分があることが次のようにして示される。
 |
例えば、 Ｌ1 と Ｌ2 が重なっていることを示す。
Ｃに属する点Ｐは、Ｃ1、Ｃ2 にも属する。
円板 Ｃ1、Ｃ2、 Ｃｋ＋1 は重なる部分があるの
で、そこに点Ｑをとる。このとき、線分ＰＱは直線
Ｌ と点Ｒで交わり、点Ｒは、円板 Ｃ1、Ｃ2 に属す
る点である。 |
したがって、点Ｒは、線分 Ｌ1、Ｌ2 に共通する点で、Ｌ1 と Ｌ2 は重なっている。
同様にして、他のどんな２つの線分に対しても重なる部分のあることが示される。
よって、補題Ａにより、線分 Ｌ1、Ｌ2、・・・、Ｌｋ に共通する点Ｄが存在する。この点
Ｄは、ｋ 個の円板 Ｃ1、Ｃ2、・・・、Ｃｋ に共通する点であるので、点Ｄは、Ｃに属さな
ければならない。しかし、このことは、Ｄの取り方に矛盾する。
ゆえに、Ｃ と Ｃｋ＋1 は重なり、ｋ＋１ 個の円板 Ｃ1、Ｃ2、・・・、Ｃｋ、Ｃｋ＋1 に共通
する点が少なくとも一つ存在する。
以上から、ｎ＝ｋ＋１ のときも成り立ち、３以上の全ての自然数に対して、命題は
成り立つ。（証終）
さて、いよいよヤングの定理の証明にとりかかろう。
平面上の ｎ 個の点から任意に３点をとる。どの２点間の距離も １ 以下であるので、一
般性を失うことなく、３点のうち１点は半径１の円の中心で、もう１点は、その円の半径上
にあるものとしてよい。そうすると、第３の点は、下図の斜線部分の領域内になければなら
ない。
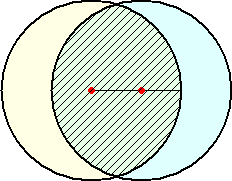
このとき、図形の対称性から、第３の点は、下図の斜線部分の領域にあるものとしてもよ
い。
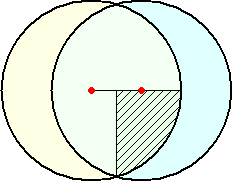
下図のように領域は、第１、第２の点を含む半径 /３ の円により被覆されるので、
第３の点がこの領域内のどこにあろうとも、３点は必ず半径 /３ の円の周および内
部に含まれる。
（厳密には計算をしなければいけないが、ここでは図による了解に留める。）
いま、平面上の ｎ 個の各点を中心として、半径 /３ の円を描く。
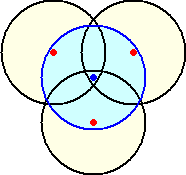
このとき、任意の３点は、半径 /３ の円の周および内部に含まれるので、その中心
は３つの円の共通部分に含まれる点である。
よって、平面上の、ｎ 個の円板のうち、どの３つの円板も重なる部分のあることが示され
た。したがって、補題Ｂにより、全ての円板に共通する点が少なくとも一つ存在する。
この点を中心として、半径 /３ の円を描けば、平面上の ｎ 個の点は全て、この円
の周および内部に含まれる。
（参考文献：ゴロヴィナ、ヤグロム 著 松田信行 訳 幾何の帰納法 （東京図書））