・ ある図形の性質 S.H氏
最近、数学の本を読んでいたら、次のような図形(緑色部分)に対して、面白い性質があるこ
とを知った。
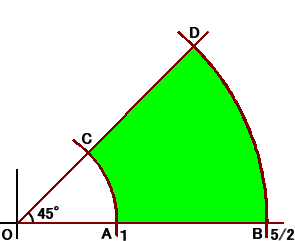
ここで、C、D の座標は、それぞれ
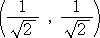 、
、 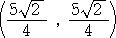
である。
この図形の外接円の直径は 2 より大きいが、図形上の任意の2点間の距離は 2
より小
さい。
前半部分は簡単に示せるので、ここでは後半部分を示すことにする。
図形上の任意の2点を、
P(acosθ,asinθ) 、 Q(bcosφ,bsinφ) ただし、 1
≦ b ≦ a ≦ 5/2
とする。
このとき、余弦定理により、 PQ2 = a2+b2−2abcos(φ−θ)
ここで、−45°≦φ−θ≦45°なので、
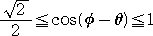
よって、
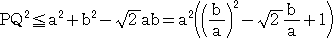
| ここで、 |
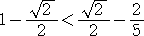 |
なので、 |
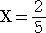 |
のとき、 |
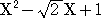 は最大となる。 したがって、 は最大となる。 したがって、 |
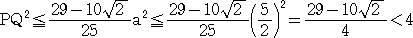
より、
PQ<2
であることが分かる。
この図形の性質を用いると、次のことが示される。
半径が 5/2 の円の周および内部に、10個の点を自由に配置すると、そのうちの
少なくとも2点は、互いの距離が2より小さい。
証明には、「鳩ノ巣原理」が用いられる。(「鳩ノ巣原理」については、こちらを参照)
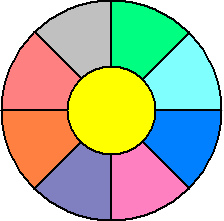 左図のように、円を分割する。ただし、中心の円は
左図のように、円を分割する。ただし、中心の円は
半径が1とし、円周は含まないものとする。その周辺
の8つの小図形が、上で取り上げられた図形で、周
および内部を考える。
このとき、鳩ノ巣原理により、少なくとも2点を含む
図形が、1個以上ある。
その2点について、明らかに互いの距離は2より小
さい。
(追記)
2004年3月2日付けで、当HPの掲示板「出会いの泉」にデニチェンさんから、
数学感動秘話の『ある図形の性質』についてですが、お互いの距離がみんな2以上
となるような9個の点の取り方はあるんでしょうか?
という質問があった。
早朝のバタバタしている時間ということもあり、デニチェンさんの真意を汲み取らずに、見
当違いのことを掲示板の方に書き込んでしまった。直感的には出来ないだろうということで、
そのときは納得していたが、とんでもない勘違いであることに後で気づかされた。
デニチェンさんは、多分、次のようなことを考えておられるのだろう。
半径が 5/2 の円の周および内部に、10個の点を自由に配置すると、そのうちの
少なくとも2点は、互いの距離が2より小さいことは鳩ノ巣原理により明らかであるが、
同じ円上で互いの距離が2以上となるような点の個数を追っていくとき、
2個 、3個 、・・・、7個 、8個
までは配置が可能である。9個の配置の可能性はあるのだろうか?
たとえば、8個の場合については、次のように配置すればよい。
(下図では、小円の半径はすべて 2 としてある。)
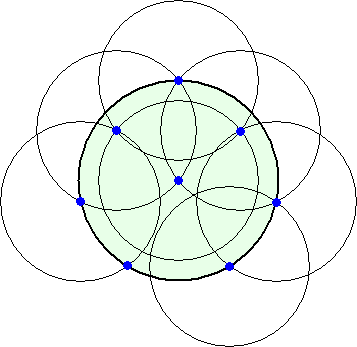
デニチェンさん同様、私も条件を満たすような形で9個の点を配置することは不可能と思
うが、いざ、その証明は?と問われてしまうと考えてしまう。鳩ノ巣原理は、ある条件を満た
すものが存在することを証明する場合に用いられるが、この問題からも分かるように比較
的緩やかな条件でしか証明をしていないということを実感させられた。
9個の点を配置することが不可能であるということを、鳩ノ巣原理を用いて証明することは、
果たして可能なのであろうか?
そういうわけで、今現在証明については検討中です!
この件で、何か情報をお持ちの方、こちらまで、メールにてご教示下さい。
(追々記) ちょっと多忙な時期と重なり、この問題の検討が「ツンドク」状態で、そのままに
なっていた。最近、デニチェンさんからメールをいただき、この問題の存在を思い
出した。その間、らすかるさんやデニチェンさんを始め、いろいろな方からアドバ
イスを伺って、いつかはアップロードをと思っていたが、超多忙に身を任せていた
ため、十分すぎる時が経ってしまった。らすかるさんやデニチェンさんにご心配を
おかけし、大変申し訳なく思っている。ここでは、らすかるさんとデニチェンさんの
解答を参考に再検討してみたいと思う。(H16.8.4)
らすかるさんから、「9個の点の配置が不可能であることを、鳩ノ巣原理を用いては証明
できない」ということをお教えいただいた。(H16.3.20)
証明の概要は次の通りである。
鳩ノ巣原理を用いて、9個の点の配置が不可能であることを示すには、半径が
5/2 の
円を、「領域内の任意の2点間の距離が2より小さい」という性質を持つ 8個の領域に分
けられなければならない。
上記の性質を持つ領域と円周との交わりを考えた場合、円周の端点を結ぶ弦の長さは
2より小さい。
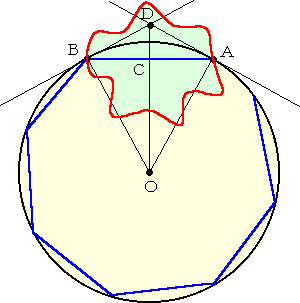 そこで、円周上に長さが2の弦を引い
そこで、円周上に長さが2の弦を引い
ていくと、弦は、8個以上必要である。
実際に、△OAC∽△ADC より、
OA : OC = AD : AC なので、
5/2 : 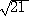 /2 = AD : 1
/2 = AD : 1
よって、
AD=5/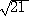
ところで、
2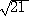 >9 であるので、
>9 であるので、
AD<10/9
従って、弦の長さ2に対する円弧の長
さは、20/9 より小さいので、弦7つ分の
円弧の長さは、140/9 より小さい。
ところが、円周の長さは、2π・(5/2)=5π で、 5π>140/9 なので、弦7つ分の円弧で
は円周全てを覆えない。
よって、上記の性質を持つ領域で、特に円周上の2点を結ぶ弦の長さが2より小さいもの
は、最低8個必要である。また、このような領域は円の中心Oを含まないので、中心を含む
別な領域が必要である。
したがって、所要の条件を満たすためには、領域は、最低 9個必要であることが分かる。
以上から、半径が 5/2 の円を、「領域内の任意の2点間の距離が2より小さい」という性
質を持つ 8個の領域に分けることは不可能であることが示された。
よって、9個の点の配置が不可能であることを、鳩ノ巣原理を用いて証明することは不可
能である。
上記の証明では、「9個の点の配置が可能なのか、不可能なのか」は、何も教えてくれな
い。ただ、鳩ノ巣原理は、この問題については使えないということを確認するのみである。
「9個の点の配置が可能なのか、不可能なのか」という問いに対して、デニチェンさんは、
次のように考えられた。
10個の点の時と同様に、円を左下図のように区切る。今、そこに、条件を満たすように
9個の点が配置されたものと仮定する。このとき、この9個の点は、全ての枠内に1個ず
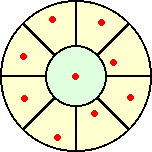
つ存在しなければならない。さらに、区切りの数を増やして
いくと、結局は下図のように、放射線状の線の上に点がな
ければならないことになる。
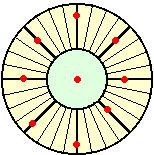
しかし、このことは条件に矛盾する。
したがって、半径5/2の円にお互いの距離が2以上となるように9個の点をとることは不
可能である。
(コメント:デニチェンさんの証明の急所は、「条件を満たすように、9個の点が配置された
ものと仮定する」という部分だろう。そして、区切りの数を増やすことによって、
点の位置を特殊化し、そのような点の配置はありえないことを示している。
極限操作が入っているので、証明としてしっくりこない面があるのだが、読者の
皆さんのご意見を伺いたい。)
(追々々記) らすかるさんから、H16.8.5付けメールにて、「半径5/2の円にお互いの
距離が2以上となるように9個の点をとることは不可能である。」ことの証明を
いただきました。「なるほど!」という証明で、感心しております!
らすかるさん、ありがとうございました。
 (準備) 半径5/2の円Oの円周上に点Pをとり、点Pを中心
(準備) 半径5/2の円Oの円周上に点Pをとり、点Pを中心
とする半径2の円を描く。円Pは、点Pによって他の
点が配置出来なくなる範囲を示す。この時の円Oと
円Pの重なった領域を領域Dとする。
ここで、連立方程式 X2+Y2=(5/2)2
X2+(Y−5/2)2=22
を解くと、円Oと円Pの交点を通る直線の方程式は
Y=17/10 となる。
したがって、この直線に関して点Pと対称な点をQ
とすれば、
OQ=5/2−2(5/2−17/10)=9/10
いま、この点Pを点Oの方向に動かす。すると、円
P、すなわち、他の点が配置出来ない範囲が少しず
つ拡がるが、OP≧OQ の範囲において、領域Dは
常に、円Pに含まれる。
(本題) もし、9個の点が配置出来たとする。点Oを中心とする半径9/10の円の中には、最
大 1個しか点は存在し得ない。よって、小円の外に、8個または9個存在する。
上記の準備により、半径9/10の円より外側にある点の、他の点が配置出来ない範
囲の最小領域は、円周上にある場合である。すると、少なくとも8点が円周上に配置
されることになるが、上図からも分かるように、弦の長さの関係から、円周上に8点を
配置することは不可能である。これは矛盾である。
従って、条件を満たすように、9個の点を配置することは出来ない。
(コメント:らすかるさんの証明は鮮やかですね!感動しました。なんとなく3月以来のモヤモ
ヤがとれたような気がします。
でも、8個全部を円周上ではなくて、円内でも可として、上図の8番目の点が領域D
に属さないようにはできないのでしょうか? また、新たな疑問です!)


 左図のように、円を分割する。ただし、中心の円は
左図のように、円を分割する。ただし、中心の円は
 そこで、円周上に長さが2の弦を引い
そこで、円周上に長さが2の弦を引い

 (準備) 半径5/2の円Oの円周上に点Pをとり、点Pを中心
(準備) 半径5/2の円Oの円周上に点Pをとり、点Pを中心