デカルトの円定理 
3つの円が互いに外接し、さらに、第4の円がこれらの3つの円に外接する場合を考える。
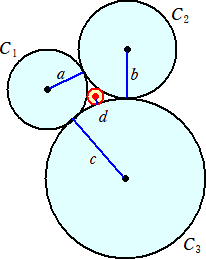
上図のように、4つの円の半径をそれぞれ a、b、c、d とすると、
(1/a+1/b+1/c+1/d)2=2(1/a2+1/b2+1/c2+1/d2)
という等式が成り立つ。ここで、1/(円の半径)は、その円の曲率と言われる。
A=1/a、B=1/b、C=1/c、D=1/d とおくと、各円の曲率A、B、C、Dにより、上記の
等式は、
(A+B+C+D)2=2(A2+B2+C2+D2)
と書き表される。この等式は、デカルトの円定理と言われ、ルネ・デカルト(1596〜1656)が
1642年に発表したとされる。
この等式は、1936年にフレディック・ソディにより再発見され、4つの円はソディの円とも
言われる。
例 半径1の3つの円に外接する円の半径を求めよ。
実際に、3つの円の中心を結ぶ正三角形の1辺の長さは、2なので、高さは、 で、
で、
円の中心は、高さを2:1に内分することから、求める円の半径は、  ×(2/3)−1
×(2/3)−1
デカルトの円定理を用いると、次のように求められる。
(1+1+1+D)2=2(1+1+1+D2)
から、 D2−6D−3=0 なので、 D=3±2
D>0 なので、 D=3+2
よって、 d=1/(3+2 )=(2
)=(2 −3)/3=
−3)/3= ×(2/3)−1 で一致する。
×(2/3)−1 で一致する。
デカルトの円定理は、曲率の2次方程式を解く形になるので、当然、正の解ばかりでなく、
解が0になったり、負の解になる場合も考えられる。
解が0の場合は、円は、直線と考えるのが自然だろう。負の解の場合は、下図のように、
3つの円が内接する場合と考える。
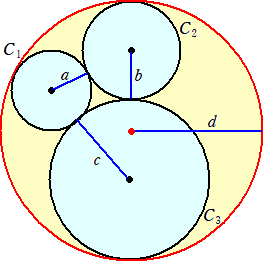
円C3が直線の場合、「フォードの円」の問題となる。「フォードの円」において
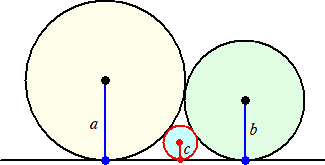 |
半径aの円と半径bの円が外接し、さ
らに共通の直線にも接している。
その2つの円と接線に接する半径c
の円がある。このとき、
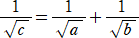 |
が示されたが、この事実は、デカルトの円定理を用いて、次のように示される。
(A+B+C+D)2=2(A2+B2+C2+D2)
において、C=0 とすると、 (A+B+D)2=2(A2+B2+D2)
両辺を展開して、Dの2次方程式 D2−2(A+B)D+(A−B)2=0
よって、解の公式より、 D=A+B±2√(AB) となる。
すなわち、 D=(√A±√B)2 より、 √D=√A±√B
「+」の方を採用すると、A=1/a、B=1/b、D=1/c を代入して、
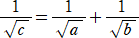
が成り立つ。
(コメント) 「フォードの円」で示されている通り、中心間の距離で示した方が簡単かな?
ここで、読者のために練習問題を残しておこう。
練習問題 半径1、3、12の3つの円が外接している。この3つの円に外接する円の半径
を求めよ。
(解) 求める円の半径を r とすると、デカルトの円定理より、
(1+1/3+1/12+1/r)2=2(1+1/9+1/144+1/r2)
すなわち、 (17/12+1/r)2=2(161/144+1/r2)
よって、 289/144+17/6・(1/r)+(1/r)2=322/144+2(1/r)2 より、
(1/r)2−17/6・(1/r)+11/48=0
このとき、 (1/r−11/4)(1/r−1/12)=0 を解いて、 r=4/11、12
# ここで、r=4/11 が直感的に求める解だと分かるが、r=12も解になるという。これは、
3つの円とどのように接する円なのだろうか、一瞬ちょっと戸惑いがある。
実は、下図のような位置関係になっている。
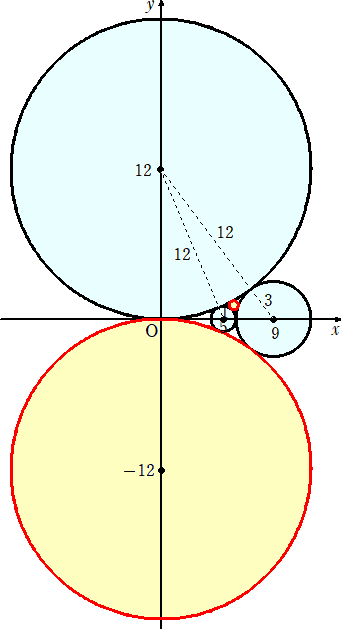
上図は、3つの円
中心(0,12)で半径12の円 、中心(5,0)で半径1の円 、中心(9,0)で半径3の円
に対して、求める円が、
中心(64/11,12/11)で半径4/11の円 、中心(0,−12)で半径12の円
であることを示す。
なるほど!こういう外接の仕方もあるんですね...。正直に告白すると、小さい方の円ば
かりに目が行っていました。
GAI さんからのコメントです。(令和3年7月29日付け)
整数の半径をもつ、3つの円が外接しているとき、第4の円が、このどれにも外接できるも
のが2つ存在し、その半径が有理数となるそれぞれの円の半径の組合せを調べてみたら、
(a,b,c) =(1,6,14) -> r1=21/5、r2=21/47
=(1,8,9) -> r1=72/17、r2=72/161
=(2,9,11) -> r1=198/7、r2=198/271
=(2,10,15) -> r1=15、r2=15/19
・・・・・・・・・・・・・・・・・・・・・・・・
などが可能のようです。(a,b,c)=(1,3,12) の r1=12、r2=4/11 は、このパターンの代表として
ベストなものですね。
以下、工事中!




