六点円について　　　　　　　　　　　　　　　　　　　　　

　三角形の特別な点を通る円として「九点円」が有名であるが、最近、「六点円」という円の
存在を知った。

△ＡＢＣにおいて、３垂線の足を Ｄ、Ｅ、Ｆ とし、

　　　　　３点 Ｄ、Ｅ、Ｆ から各辺に下ろした垂線の足

の合計６点は、同一円周上にある。この円のことを、六点円という。

　六点円は、Ｈｅｎｒｙ Ｍａｒｔｉｎ Ｔａｙｌｏｒ（1842〜1927）の名に因んで、Ｔａｙｌｏｒ円とも呼ばれる。



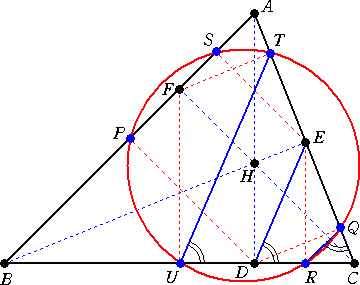
　　　　左図において、

　　　　　　Ｈは△ＡＢＣの垂心













（証明）　４点 Ｔ、Ｑ、Ｒ、Ｕ が同一円周上にあること　：　∠ＣＱＲ＝∠ＣＵＴ　を示せばよい。

　　　　４点 Ｑ、Ｒ、Ｄ、Ｅ が同一円周上にあるので、　∠ＣＱＲ＝∠ＣＤＥ

　　　　また、△ＣＤＥと△ＣＵＴにおいて、　ＣＤ ： ＣＵ＝ＣＨ ： ＣＦ＝ＣＥ ： ＣＴ　なので、

　　　　△ＣＤＥ∽△ＣＵＴ　となり、　∠ＣＤＥ＝∠ＣＵＴ　である。

　　　　よって、　∠ＣＱＲ＝∠ＣＵＴ　となるので、４点 Ｔ、Ｑ、Ｒ、Ｕ は同一円周上にある。

　　　同様にして、４点 Ｐ、Ｕ、Ｒ、Ｓ も同一円周上にある。

　次に、４点 Ｓ、Ｕ、Ｒ、Ｔ が同一円周上にあること　：　∠ＲＵＴ＝∠ＲＳＴ　を示せばよい。

　　４点 Ｂ、Ｃ、Ｅ、Ｆ が同一円周上にあるので、　∠ＡＢＣ＝∠ＡＥＦ

　　４点 Ｆ、Ｅ、Ｔ、Ｓ が同一円周上にあるので、　∠ＡＥＦ＝∠ＡＳＴ

　　　　よって、　∠ＡＢＣ＝∠ＡＳＴ　となるので、ＢＣとＳＴは平行で、　∠ＢＲＳ＝∠ＲＳＴ

　　４点 Ａ、Ｆ、Ｄ、Ｃ が同一円周上にあるので、　∠ＢＤＦ＝∠ＦＡＴ

　　　　すなわち、　∠ＢＤＦ＝∠ＲＵＴ

　　また、上記と同様にして、　△ＢＤＦ∽△ＢＲＳ　なので、　∠ＢＤＦ＝∠ＢＲＳ

　　　以上から、　∠ＲＵＴ＝∠ＲＳＴ　となり、４点 Ｓ、Ｕ、Ｒ、Ｔ が同一円周上にある。

　　よって、６点 Ｐ、Ｑ、Ｒ、Ｓ、Ｔ、Ｕ は、同一円周上にある。　（証終）

（コメント）　スッキリした証明を目指したつもりですが、何となくフラフラしているような．．．。