円の詰め込み 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　ある決まった図形に円とか球を詰め込む問題は適度な入試問題になりやすい。最近解
いたもので、１９９８年度の東京工業大学の入試問題は適度に面白い問題だった。考えよ
うによっては、中学校数学レベルかもしれない。近頃、難関と言われる大学ほど、ときどき
中学校数学レベルの問題を平気で出題するから困ったものだ！
　　　　　　　　　　　　　　　　　　　　　　　（例えば、平成２０年度前期京都大学　など．．．。）

東京工業大学　前期（平成１０（１９９８）年度）

　Ｒを、隣り合う２辺の長さ ａ 、 ｂ が ２ａ＞ｂ＞ａ をみたす長方形とし、Ａを、次の性
質（Ｐ）を持つ半径 ｘ の円とする。

　　（Ｐ）　Ｒの内部にあって隣り合う２辺にだけ接する。

（１） 性質（Ｐ）を持つ円で円Ａに外接するものが４つ存在するために、円Ａの半径 ｘ
　　がみたすべき条件を ａ 、 ｂ を使って表せ。

（２） ｘ が（１）の条件をみたすとき、円Ａに外接する４つの円のうち２番目に大きい
　　円をＢとする。 ｘ が変化するとき円Ａと円Ｂの面積の和の最小値を求めよ。

　上記の（１）は中学校数学レベルで解きうる問題だろう。

　ａ＝８、ｂ＝９　と問題を具体化して考えることにしよう。一般の場合も解法は同様である。

　Ｒを、縦、横の長さがそれぞれ ８ と ９ である長方形とし、Ａを、次の性質（Ｐ）を持
つ半径 ｘ の円とする。

　　（Ｐ）　Ｒの内部にあって隣り合う２辺にだけ接する。

（１） 性質（Ｐ）を持つ円で円Ａに外接するものが４つ存在するために、円Ａの半径 ｘ
　　がみたすべき条件を求めよ。

（２） ｘ が（１）の条件をみたすとき、円Ａに外接する４つの円のうち２番目に大きい
　　円をＢとする。 ｘ が変化するとき円Ａと円Ｂの面積の和の最小値を求めよ。
　　　　　　　　　　　　　　　　　　（（２）は、微分積分の範疇なので、中学生には無理かな？）

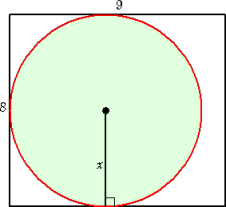
（解）（１）　この場合の解法のポイントは極端な場合を考えることであろう。

ｘ が最大となるのは、右図のように　　 　　　　円Ａが目一杯に拡張する場合である。 　　　　　よって、題意より、 　　　　　　　　　ｘ＜４ 　　　　となる。
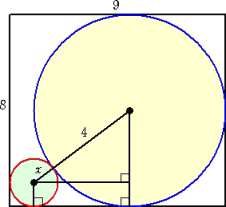	ｘ が最小となるのは、左図のように 円Ａに接する右側の円が目一杯に拡 張する場合である。 　三平方の定理より、 （ｘ＋４）2＝（５−ｘ）2＋（４−ｘ）2 これを解いて、

　　　　　　　　　　　ｘ²＋８ｘ＋１６＝２５−１０ｘ＋ｘ²＋１６−８ｘ＋ｘ²

　　　　　　　　　　　　　　　　ｘ²−２６ｘ＋２５＝０

　　　　　　　　　　　（ｘ−１）（ｘ−２５）＝０　より、　ｘ＝１、２５

　　　　　　　　　　　　　　０＜ｘ＜４　なので、　ｘ＝１

　以上から、求める ｘ の値の範囲は、　１＜ｘ＜４


（２）　面積が２番目に大きい円は、下図のように配置している。

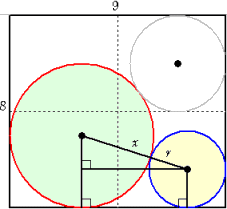このとき、　（ｘ＋ｒ）2＝（ｘ−ｒ）2＋（９−ｘ−ｒ）2 　　（ｘ＋ｒ）2＝ｘ2−２ｒｘ＋ｒ2＋８１−１８（ｘ＋ｒ）＋（ｘ＋ｒ）2 　　　　　ｒ2−２（ｘ＋９）ｒ＋（ｘ−９）2＝０ 　　ｒ＜９　なので、　ｒ＝ｘ＋９−６√ｘ＝（√ｘ−３）2 　　よって、円Ａの面積＋円Ｂの面積をＳとすると、 　　　Ｓ＝πｘ2＋πｒ2＝π（ｘ2＋（√ｘ−３）4）

　√ｘ＝ｔ　とおくと、　１＜ｔ＜２　で、　Ｓ＝π（ｔ⁴＋（ｔ−３）⁴）

　　　　　Ｓ’＝π（４ｔ³＋４（ｔ−３）³）

　　　　　　＝４π（ｔ＋ｔ−３）（ｔ²−ｔ（ｔ−３）＋（ｔ−３）²）

　　　　　　＝４π（２ｔ−３）（ｔ²−３ｔ＋９）＝０　より、　　　ｔ＝３/２

　ｔ＝３/２　でＳは極小かつ最小で、最小値は、８１π/８　（終）

　　同様の趣旨の問題を空間に拡張して考えてみよう。

　１辺の長さが４の立方体の８つの隅で、半径１の球を、１点で交わる３平面の何れ

にも接するように配置する。このとき、８つの球の何れにも外接する球Ｓを考える。

　このときの球Ｓの半径を求めよ。

　空間把握がしっかりしていれば何でもない問題だが、頭の中に図形がイメージできないと
少し辛いかもしれない。

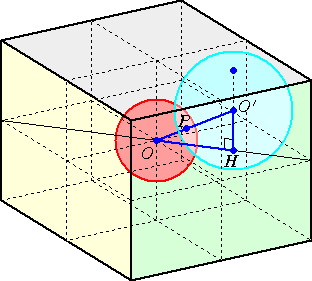　　左図は、８つの隅に接する半径１の球
　のうちの一つが球Ｓと接する状況を示し
　たものである。

　　　　直角三角形ＯＨＯ’において、

　　　三平方の定理より、

　　　　　　　ＯＨ²＋Ｏ’Ｈ²＝ＯＯ’²

　　　すなわち、球Ｓの半径を ｒ とすると、

　　　　　　　²＋１²＝（ｒ＋１）²

　　　これより、　ｒ＝−１　となる。






　　以下、工事中