球帯と球冠　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　球帯とは球面を平行な二平面で切ったときに、その二平面に挟まれる球面の部分を言う。
このとき、上面（上底）は半径 ａ の円、底面（下底）は半径 ｂ の円である。
　　　　　　

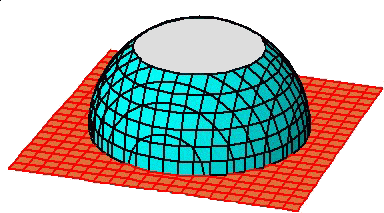
　特に、　ａ＝０　であるような球帯を、球冠と言う。

　この球帯の高さを ｈ とすると、側面積 Ｓ は、非常に美しい形で表される。

　　　　　　　　　　

ただし、ｒ は、側面の球の半径とする。

　この公式を、　　　と分解して考えれば、

　　　　　　（大円の周の長さ）×（球帯の高さ）

という形で表現することができる。

例　原点中心で半径 ３ の球を平面　ｚ＝１　、　ｚ＝２　で切ったときに出来る球帯の側面
　積を求めよ。

　　上記の公式を知っていれば、複雑な計算をすることなく、　２π×３×１＝６π　と即答
　だろう。

（公式の証明）
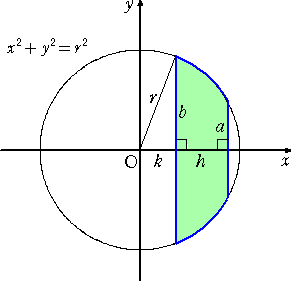　　左図において、

　　　　

　　ここで、　ｘ²＋ｙ²＝ｒ²　より、　ｙ’＝−ｘ/ｙ

　より、
　　　　　

　となる。
　　　　　　　　　　　　　　　　　　　（証明終）




（コメント）　球帯の側面積が、上底、下底の半径に無関係に、高さと球の半径のみで定ま
　　　　　　るところが面白いですね！


（追記）　上記に関連する話題で、「リンゴの皮むき」と題して、当ＨＰがいつもお世話になって
　　　　　いるＨＮ「ＧＡＩ」さんからのご投稿です。（令和３年３月２８日付け）

　ある大きさの球体を真二つに切り、更にその一方の半球を更に半球の高さの半分の位置
で切断して２つに分けた。こうしてできた２つをK1、K2とする。（切断面が一つの方をK1として
おく。）

　元々球体の表面にある部分のK1とK2での表面積をS(K1)、S((k2)で表したとき、

　　S(K1) ： S(K2)

はどの様になるか？

　完璧に球体であるリンゴを半分の半分としたリンゴのそれぞれの皮をむいたら、さてどちら
の皮の面積がどれだけ大きくなるか想像してみよう。


（コメント）　計算するまでもなく、冒頭の球帯の公式から、S(K1) ： S(K2)＝１ ： １　ですね！


　 ＧＡＩさんからのコメントです。（令和３年３月２９日付け）

　正解です。

　体積の大きさ(5：11)に引きずられて、計算で求めるまで同じになることが気付けませんでし
た。従って、球のリンゴの直径をｎ等分した各物体の皮の表面積は全部同じ値を持つんです
ね。


　カルピスさんからのコメントです。（令和３年３月２９日付け）

　円の場合も同じように考えて良いですか？円の直径をｎ等分したら、ｎ個の面積は全て同
じですか？


　らすかるさんからのコメントです。（令和３年３月２９日付け）

　球の表面積がそれに接する円柱の側面積に等しいのは、微小部分を円柱に投影したとき
に面積が変わらないためですが、それは、

「赤道から離れるにつれて断面の半径が小さくなるために、経度方向の長さが√(r^2-x^2)/r
倍に小さくなること」

と

「赤道から離れるにつれて面が傾いていくために、緯度方向の長さがr/√(r^2-x^2)倍に大
きくなること」

の二つで相殺されるためです。

　よって、円では同様のことは起こりません。円の場合は、スライスしたとき、

・面積は√(r^2-x^2)/r倍に小さくなる
・弧長はr/√(r^2-x^2)倍に大きくなる

のように独立して変化します。


　カルピスさんからのコメントです。（令和３年３月２９日付け）

　らすかるさん、有難うございます。

　先程、方眼紙で作図してみたら、どう見ても、大きさが同じ訳ないなと思いました。直径か
ら離れる程、面積は小さくなっていくのですね。


　ＧＡＩさんからのコメントです。（令和３年３月３０日付け）

　カルピスさん、ピザなら外側のカリッカリ部分は同じ長さになります。


　スモークマンさんからのコメントです。（令和３年３月３１日付け）

　円の直径を４等分した時、外側は中心角120°、内側は、60°なので、

　　外1/4の円弧の長さ ： 内1/4の円弧の長さ＝２ ： １

になりませんでしょうかしらん...? 間違ってたらごめんなさい。


（コメント）　「ピザなら」と条件が付いているので、４つに分けるのではなく、６等分をイメージ
　　　　　　しているのでは？


　ＧＡＩさんからのコメントです。（令和３年４月１日付け）

　いえいえ、当方の全くの勘違いでした。直径を4等分しておいて、外周を見る時、中の２つの
部分を合わせて観察してしまっていました。確かに、２：１の比でしたね。


　Dengan kesaktian Indukmuさんからのコメントです。（令和３年３月３０日付け）

　このページがコンパクトにまとまっていて参考になりますね。円帯でググってみても面白い
です。

　たとえば、「円と帯の共通部分の面積」が、このページの内容と照応がとれていて興味深
いです。


（閑話休題）

　球帯の側面積の公式を、半径 ｒ の球に適用すれば、球の表面積の公式が得られる。

　　　左図において、

　　　　　　（大円の周の長さ）＝２πｒ

　　　　　　（球帯の高さ）＝２ｒ

　　　なので、球の表面積は、

　　　　（大円の周の長さ）×（球帯の高さ）＝４πｒ²



　また、球冠については次のような驚嘆に値する美しい公式が成り立つ。

　　左図の球冠において、側面積 Ｓ は、

　　　　

　で与えられる。

　　証明は易しい。

　　（ｒ−ｈ）²＋ｂ²＝ｒ²　より、

　　　　　　２ｒｈ＝ｈ²＋ｂ²＝Ｒ²

　　よって、　　が成り立つ。





（コメント）　球冠も上底側から眺めると円なわけで、その面積が、円の公式っぽい式で与え
　　　　　　られるところが数学らしいですね！

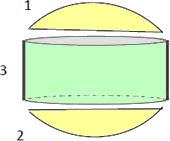
　球冠の側面積が、Ｒのみで定まることから、次の性質が導かれることは自明だろう。

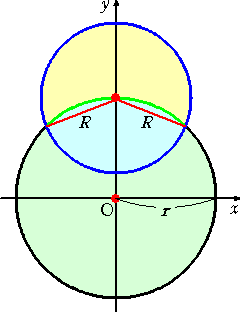　左図において、半径 Ｒ の球と半径 ｒ の球が交わり
かつ、半径 ｒ の球は半径 Ｒ の球の中心を通るものと
する。

　このとき、半径 ｒ の球の半径 Ｒ の球の内部にある
部分の表面積は、ｒ の値によらず一定で、

　　　　　　　　　　πＲ²

で与えられる。

（追記）　平成２１年７月１１日付け

　　当ＨＰの掲示板「出会いの泉」に、７月９日付けで、ＨＮ「ゆっきもも」さんから質問が寄せ
られた。

　　任意の位置でスライスした（正確な半球でないもの)場合の表面積の求め方を教え
　てください。

　この問いかけに対して、当ＨＰがいつもお世話になっている、らすかるさんが明解に回答
された。（平成２１年７月１０日付け）

　　球を同じ幅でスライスすると、それぞれの側面積は同じになる。

　　よって、直径のどの位置で切ったかが分かれば、

　　　４πｒ²×(直径を切り取った長さ)/(直径) = ２πr×(直径を切り取った長さ)

　　で求まる。

（コメント）　らすかるさんの求めた側面積に上底、下底の面積を加えれば、表面積は求め
　　　　　　られる。

　　このページの冒頭で、次の公式

　　　球帯の高さを ｈ とすると、側面積 Ｓ は、　　

　　　（ただし、ｒ は、側面の球の半径）

　を定積分計算で示したが、らすかるさんのように考えると、この公式も覚えやすいですね！


　また、当HPがいつもお世話になっているＨＮ「凡人」さんも球冠の場合についての解答
を寄せられた。（平成２１年７月１０日付け）（←若干文言等を修正させていただきました）

　　半径Ｒの球を、中心からの距離ｄで切った図形（の小さい方）とする。

　　　　

　　側面積を Ｓ とおくと、

　　　

　これに、断面積のπ（Ｒ²−ｄ²）を足して、求める表面積は、π（Ｒ−ｄ）（３Ｒ＋ｄ）　となる。

　一応確認のために、ｄ＝０　とした時は、半球の表面積と一致し、ｄ＝−Ｒ　とすると、全球
の表面積になる。

（コメント）　凡人さん、ありがとうございます。重積分した２πＲ²（１−ｄ/Ｒ）という結果は、上
　　　　　　記で得られた公式より求められる　２πＲ（Ｒ−ｄ）　とも一致していますね！

　　　　　　上記では、球冠の側面積を重積分で求めたが、高校の数学�Vの範囲で十分求め
　　　　　られる。むしろその方が普通かも．．．。
　　　　　（随分昔に東大の入試問題に出題されたかな？）


　当ＨＰをご覧になった Ｙ．Ｓ．さんから、次のような質問をメールでいただいた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年７月１９日付け）

　錠剤の表面積を計算したいと思います。錠剤を次のように


　　1． Upper Biconvex dome

　　2． Lower Biconvex dome

　　3． Middle cylinder




と、３つの部分に分けて考えた場合、1と2の半径と表面積は、以下の計算式

　　radius　of　curvature　ｒ_ｃ　given　by　ｒ_ｃ＝（ｈ²＋（ｄ/２）²）/（２ｈ）
　where　ｄ　is　the　diameter　and　ｈ　is　the　height．

　　Surface　area　of　a　spherical　dome’s　ceiling　is　Ａ＝２πｒ_ｃｈ．

により求められるとあるのですが、何故、このような計算式になるのか分かりません。

　Ｙ．Ｓ．さんの質問に答えて、計算してみた。

（計算）　上面の球冠を、曲率半径 ｒ_c の球面の一部と考え、球冠の底円の直径を ｄ とし、

　　　　　底円から球冠の頂上までの距離を ｈ とする。

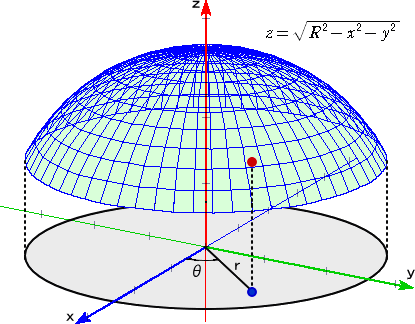
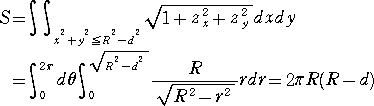
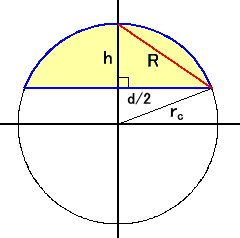　　　左図において、三平方の定理より、

　　　　　（ｒ_c−ｈ）²＋（ｄ/２）²＝ｒ_c²

　　　よって、　２ｒ_c・ｈ＝ｈ²＋（ｄ/２）²　より、

　　曲率半径 ｒ_c は、

　　　　　　ｒ_c＝｛ｈ²＋（ｄ/２）²｝/２ｈ

　　により与えられる。




　このとき、球冠の表面積の公式　：

　　　　　　　　球冠の高さを ｈ とすると、側面積 Ｓ は、　　

　　　　　　　　　（ただし、ｒ は、側面の球の半径）　　　（※　証明はこちら）

により、求める表面積Ａは、　Ａ＝２πｒ_cｈ　により与えられる。



　　　　以下、工事中！