立体の表面積 
2次関数の最大・最小の問題で、次の問題は有名だろう。
周の長さが一定な長方形のうち面積が最大なのは、正方形のときである
(→ 参考:「周の長さ一定な図形」)
例 長さ8mのロープで長方形の土地を囲む。どのように囲ったら面積は最大になるか?
(解) 長方形の縦の長さを x mとすると、横の長さは、4−x mである。
長方形の面積を y m2 とすると、
y=x(4−x)=−x2+4x=−(x−2)2+4 ただし、0<x<4
よって、x=2 のとき、面積は最大となる。
このとき出来る図形は、1辺の長さ 2 mの正方形である。 (終)
この事実は、次のことを我々に示唆する。すなわち、
同じ面積の長方形においては、正方形の場合が最も周の長さは短い
このことを、立体の場合に拡張すれば、
同じ体積の直方体においては、立方体の場合が最も表面積は小さい
とも言える。こんなことを今日この頃お昼を食べながら考えていたら、mita
さんが同趣旨の
問題を、当HPの掲示板「出会いの泉」に出題された。(平成22年10月27日付け)
1辺が 1cm の立方体がたくさんあるものとする。この立方体は切断できないもの
とする。
(1)この立方体を 64 個使って出来る立体の表面積の最小値はいくらか。
(2)この立方体を 300 個使って出来る立体の表面積の最小値はいくらか。
(3)この立方体を 2010 個使って出来る立体の表面積の最小値はいくらか。
立体は中が空洞になってはいけません。それぞれどんな図形になるでしょうか?
この問題に対して、当HPがいつもお世話になっているHN「らすかる」さんが解答を寄せら
れた。(平成22年10月27日付け)
合ってるかどうかわかりませんが...(1)96 (2)276 (3)960
(1)は立方体、(2)(3)は立方体に近い図形。
出題者の mita さんによれば、正解!とのこと。
らすかるさんの解答を目標に考えてみた。
(解) 1辺が
1cm の立方体の表面積は、6cm2 である。
(1)について、
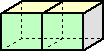 |
この立方体を2個用いる場合の立体の表面積の最小値は、
6×2−2=10cm2
である。
|
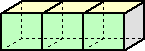
|
この立方体を3個用いる場合の立体の表面積の最小値は、
6×3−2×2=14cm2 である。
|
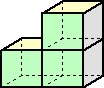
この立方体を4個用いる場合の立体の表面積の最小値は、
6×4−2×4=16cm2 である。
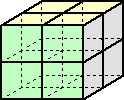
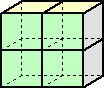
この立方体を8個用いる場合の立体の表面積の最小値は、
6×8−2×12=24cm2 である。
したがって、立方体を64個用いる場合の立体の表面積の最小値は、
24×8−8×12=96cm2 である。・・・・・・・・・らすかるさんの答えと一致!
(2)について、立方数 1、8、27、64、125、216、343、・・・ を考え、さらに、立方体
に近い立体を考えるということで、
300=216+84=216+36×2+6×2
の組合せから、
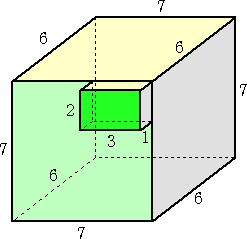
という立体を考える。緑色の直方体は、正方形上どこにあってもよい。
この立体の表面積は、276cm2 で、らすかるさんの答えと一致する!
同様に、(3)について、立方数
1、8、27、64、125、216、343、512、729、1000、1331、1728、2197、・・・
を考え、さらに、立方体に近い立体を考えるということで、
2010=1728+144+132+6=123+122+12×11+3×2
の組合せから、
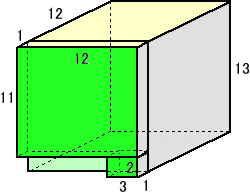
という立体を考える。緑色の直方体のうち小さい方は下部のどこにあってもよい。
この立体の表面積は、
12×12×2+13×12×4+12×2+11×2+2=288+624+24+22+2=960
から、960cm2
で、らすかるさんの答えと一致する!
らすかるさんによれば、12×13×13−18 でも 12×12×14−6 でも同じになると
のこと。
(コメント) mita さん、らすかるさんに感謝します。
当HPがいつもお世話になっているHN「FN」さんが上記の問題を一般化し、「立方体の数
が n 個」のときを考えられました。(平成22年10月28日付け)
(0) n=k3 の場合 1辺が k の立方体のとき、最小
(1) n=k2(k+1) の場合 3辺が k、k、k+1 の直方体のとき、最小
(2) n=k(k+1)2 の場合 3辺が k、k+1、k+1 の直方体のとき、最小
この3つは直感的には明らかそうです。ただ、このあたりの証明を要求されたら、どうした
らいいでしょう。明きらかそうだけど、証明となると難しそうです。なお、それぞれの場合の
表面積は、
(0) 6k2 (1) 6k2+4k (2) 6k2+8k+2
一般の n については、まず、k3≦n<(k+1)3 となる k をとる。次に、n が k2(k+1)
より大きいかどうか、k(k+1)2 より大きいかどうかを調べて、もとになる直方体を決める。
(0)(1)(2)のどれか。あとは、残った立方体を1つの面(置くことさえできればどの面でもよ
い。面積の一番大きい面にしておけば必ずおける。)の上に積んでいく。
1つ目をおくと、表面積は4増える。2つ目以降は1つの面を接するように置けば、2増える。
2つの面を接するようにおけば表面積は増えない。できるだけ増えないように、即ち正方形
を作るように、例えば、下図のような順で置いていけばよい。
(らすかるさんからのアドバイス(平成22年10月28日付け)を参考にさせていただきました。)
923
814
765
直方体を作ったあとで、残った立方体の数を R とする。
R=k2 であれば、増える表面積は、4k
R=k2+1 であれば、さらに、2増えて、R=k2+k までは増えない。
R=k2+k+1 で、また、2増えて、R=k2+2k+1=(k+1)2 までは増えない。
証明となると書きにくいですが、これで最小値は得られそうです。証明はともかく、結果ぐら
いはきちんと書きたかったのですが、うまく書けないので、ExcelのVBAで、最小値を求める
関数 M(N) を書いてみました。
Function M(N)
K = Int(N ^ (1 / 3))
L = 0
R = N - K * K * K
If R > K * K Then
L = 1
R = R - K * K
If R > K * K + K Then
L = 2
R = R - K * K - K
End If
End If
M = S(K, L) + Z(R)
End Function
Function S(K, L)
S = 6 * K * K + 4 * L * K
If L = 2 Then S = S + 2
End Function
Function Z(R)
K = Int(Sqr(R))
Z = 4 * K
R = R - K * K
If R > 0 Then Z = Z + 2
If R > K Then Z = Z + 2
End Function
FNさんの書かれたプログラムを Excel で実行し、次のような M(N)
の表が得られた。
| N |
M(N) |
|
N |
M(N) |
|
N |
M(N) |
|
N |
M(N) |
|
N |
M(N) |
| 1 |
6 |
|
101 |
134 |
|
201 |
212 |
|
301 |
278 |
|
401 |
334 |
| 2 |
10 |
|
102 |
136 |
|
202 |
212 |
|
302 |
278 |
|
402 |
336 |
| 3 |
14 |
|
103 |
138 |
|
203 |
212 |
|
303 |
278 |
|
403 |
336 |
| 4 |
16 |
|
104 |
138 |
|
204 |
212 |
|
304 |
280 |
|
404 |
336 |
| 5 |
20 |
|
105 |
140 |
|
205 |
212 |
|
305 |
280 |
|
405 |
338 |
| 6 |
22 |
|
106 |
140 |
|
206 |
214 |
|
306 |
280 |
|
406 |
338 |
| 7 |
24 |
|
107 |
142 |
|
207 |
214 |
|
307 |
282 |
|
407 |
338 |
| 8 |
24 |
|
108 |
142 |
|
208 |
214 |
|
308 |
282 |
|
408 |
338 |
| 9 |
28 |
|
109 |
142 |
|
209 |
214 |
|
309 |
282 |
|
409 |
340 |
| 10 |
30 |
|
110 |
144 |
|
210 |
214 |
|
310 |
282 |
|
410 |
340 |
| 11 |
32 |
|
111 |
144 |
|
211 |
216 |
|
311 |
284 |
|
411 |
340 |
| 12 |
32 |
|
112 |
144 |
|
212 |
216 |
|
312 |
284 |
|
412 |
340 |
| 13 |
36 |
|
113 |
146 |
|
213 |
216 |
|
313 |
284 |
|
413 |
342 |
| 14 |
38 |
|
114 |
146 |
|
214 |
216 |
|
314 |
284 |
|
414 |
342 |
| 15 |
40 |
|
115 |
146 |
|
215 |
216 |
|
315 |
286 |
|
415 |
342 |
| 16 |
40 |
|
116 |
146 |
|
216 |
216 |
|
316 |
286 |
|
416 |
342 |
| 17 |
42 |
|
117 |
148 |
|
217 |
220 |
|
317 |
286 |
|
417 |
342 |
| 18 |
42 |
|
118 |
148 |
|
218 |
222 |
|
318 |
286 |
|
418 |
344 |
| 19 |
46 |
|
119 |
148 |
|
219 |
224 |
|
319 |
286 |
|
419 |
344 |
| 20 |
48 |
|
120 |
148 |
|
220 |
224 |
|
320 |
288 |
|
420 |
344 |
| 21 |
50 |
|
121 |
150 |
|
221 |
226 |
|
321 |
288 |
|
421 |
344 |
| 22 |
50 |
|
122 |
150 |
|
222 |
226 |
|
322 |
288 |
|
422 |
344 |
| 23 |
52 |
|
123 |
150 |
|
223 |
228 |
|
323 |
288 |
|
423 |
346 |
| 24 |
52 |
|
124 |
150 |
|
224 |
228 |
|
324 |
288 |
|
424 |
346 |
| 25 |
54 |
|
125 |
150 |
|
225 |
228 |
|
325 |
290 |
|
425 |
346 |
| 26 |
54 |
|
126 |
154 |
|
226 |
230 |
|
326 |
290 |
|
426 |
346 |
| 27 |
54 |
|
127 |
156 |
|
227 |
230 |
|
327 |
290 |
|
427 |
346 |
| 28 |
58 |
|
128 |
158 |
|
228 |
230 |
|
328 |
290 |
|
428 |
346 |
| 29 |
60 |
|
129 |
158 |
|
229 |
232 |
|
329 |
290 |
|
429 |
348 |
| 30 |
62 |
|
130 |
160 |
|
230 |
232 |
|
330 |
290 |
|
430 |
348 |
| 31 |
62 |
|
131 |
160 |
|
231 |
232 |
|
331 |
292 |
|
431 |
348 |
| 32 |
64 |
|
132 |
162 |
|
232 |
232 |
|
332 |
292 |
|
432 |
348 |
| 33 |
64 |
|
133 |
162 |
|
233 |
234 |
|
333 |
292 |
|
433 |
348 |
| 34 |
66 |
|
134 |
162 |
|
234 |
234 |
|
334 |
292 |
|
434 |
348 |
| 35 |
66 |
|
135 |
164 |
|
235 |
234 |
|
335 |
292 |
|
435 |
350 |
| 36 |
66 |
|
136 |
164 |
|
236 |
234 |
|
336 |
292 |
|
436 |
350 |
| 37 |
70 |
|
137 |
164 |
|
237 |
236 |
|
337 |
294 |
|
437 |
350 |
| 38 |
72 |
|
138 |
166 |
|
238 |
236 |
|
338 |
294 |
|
438 |
350 |
| 39 |
74 |
|
139 |
166 |
|
239 |
236 |
|
339 |
294 |
|
439 |
350 |
| 40 |
74 |
|
140 |
166 |
|
240 |
236 |
|
340 |
294 |
|
440 |
350 |
| 41 |
76 |
|
141 |
166 |
|
241 |
236 |
|
341 |
294 |
|
441 |
350 |
| 42 |
76 |
|
142 |
168 |
|
242 |
238 |
|
342 |
294 |
|
442 |
352 |
| 43 |
78 |
|
143 |
168 |
|
243 |
238 |
|
343 |
294 |
|
443 |
352 |
| 44 |
78 |
|
144 |
168 |
|
244 |
238 |
|
344 |
298 |
|
444 |
352 |
| 45 |
78 |
|
145 |
168 |
|
245 |
238 |
|
345 |
300 |
|
445 |
352 |
| 46 |
80 |
|
146 |
170 |
|
246 |
238 |
|
346 |
302 |
|
446 |
352 |
| 47 |
80 |
|
147 |
170 |
|
247 |
240 |
|
347 |
302 |
|
447 |
352 |
| 48 |
80 |
|
148 |
170 |
|
248 |
240 |
|
348 |
304 |
|
448 |
352 |
| 49 |
84 |
|
149 |
170 |
|
249 |
240 |
|
349 |
304 |
|
449 |
356 |
| 50 |
86 |
|
150 |
170 |
|
250 |
240 |
|
350 |
306 |
|
450 |
358 |
| 51 |
88 |
|
151 |
174 |
|
251 |
240 |
|
351 |
306 |
|
451 |
360 |
| 52 |
88 |
|
152 |
176 |
|
252 |
240 |
|
352 |
306 |
|
452 |
360 |
| 53 |
90 |
|
153 |
178 |
|
253 |
244 |
|
353 |
308 |
|
453 |
362 |
| 54 |
90 |
|
154 |
178 |
|
254 |
246 |
|
354 |
308 |
|
454 |
362 |
| 55 |
92 |
|
155 |
180 |
|
255 |
248 |
|
355 |
308 |
|
455 |
364 |
| 56 |
92 |
|
156 |
180 |
|
256 |
248 |
|
356 |
310 |
|
456 |
364 |
| 57 |
92 |
|
157 |
182 |
|
257 |
250 |
|
357 |
310 |
|
457 |
364 |
| 58 |
94 |
|
158 |
182 |
|
258 |
250 |
|
358 |
310 |
|
458 |
366 |
| 59 |
94 |
|
159 |
182 |
|
259 |
252 |
|
359 |
310 |
|
459 |
366 |
| 60 |
94 |
|
160 |
184 |
|
260 |
252 |
|
360 |
312 |
|
460 |
366 |
| 61 |
96 |
|
161 |
184 |
|
261 |
252 |
|
361 |
312 |
|
461 |
368 |
| 62 |
96 |
|
162 |
184 |
|
262 |
254 |
|
362 |
312 |
|
462 |
368 |
| 63 |
96 |
|
163 |
186 |
|
263 |
254 |
|
363 |
312 |
|
463 |
368 |
| 64 |
96 |
|
164 |
186 |
|
264 |
254 |
|
364 |
314 |
|
464 |
368 |
| 65 |
100 |
|
165 |
186 |
|
265 |
256 |
|
365 |
314 |
|
465 |
370 |
| 66 |
102 |
|
166 |
186 |
|
266 |
256 |
|
366 |
314 |
|
466 |
370 |
| 67 |
104 |
|
167 |
188 |
|
267 |
256 |
|
367 |
314 |
|
467 |
370 |
| 68 |
104 |
|
168 |
188 |
|
268 |
256 |
|
368 |
314 |
|
468 |
370 |
| 69 |
106 |
|
169 |
188 |
|
269 |
258 |
|
369 |
316 |
|
469 |
372 |
| 70 |
106 |
|
170 |
188 |
|
270 |
258 |
|
370 |
316 |
|
470 |
372 |
| 71 |
108 |
|
171 |
190 |
|
271 |
258 |
|
371 |
316 |
|
471 |
372 |
| 72 |
108 |
|
172 |
190 |
|
272 |
258 |
|
372 |
316 |
|
472 |
372 |
| 73 |
108 |
|
173 |
190 |
|
273 |
260 |
|
373 |
316 |
|
473 |
372 |
| 74 |
110 |
|
174 |
190 |
|
274 |
260 |
|
374 |
318 |
|
474 |
374 |
| 75 |
110 |
|
175 |
190 |
|
275 |
260 |
|
375 |
318 |
|
475 |
374 |
| 76 |
110 |
|
176 |
192 |
|
276 |
260 |
|
376 |
318 |
|
476 |
374 |
| 77 |
112 |
|
177 |
192 |
|
277 |
260 |
|
377 |
318 |
|
477 |
374 |
| 78 |
112 |
|
178 |
192 |
|
278 |
262 |
|
378 |
318 |
|
478 |
374 |
| 79 |
112 |
|
179 |
192 |
|
279 |
262 |
|
379 |
318 |
|
479 |
376 |
| 80 |
112 |
|
180 |
192 |
|
280 |
262 |
|
380 |
320 |
|
480 |
376 |
| 81 |
116 |
|
181 |
196 |
|
281 |
262 |
|
381 |
320 |
|
481 |
376 |
| 82 |
118 |
|
182 |
198 |
|
282 |
262 |
|
382 |
320 |
|
482 |
376 |
| 83 |
120 |
|
183 |
200 |
|
283 |
264 |
|
383 |
320 |
|
483 |
376 |
| 84 |
120 |
|
184 |
200 |
|
284 |
264 |
|
384 |
320 |
|
484 |
376 |
| 85 |
122 |
|
185 |
202 |
|
285 |
264 |
|
385 |
320 |
|
485 |
378 |
| 86 |
122 |
|
186 |
202 |
|
286 |
264 |
|
386 |
322 |
|
486 |
378 |
| 87 |
124 |
|
187 |
204 |
|
287 |
264 |
|
387 |
322 |
|
487 |
378 |
| 88 |
124 |
|
188 |
204 |
|
288 |
264 |
|
388 |
322 |
|
488 |
378 |
| 89 |
124 |
|
189 |
204 |
|
289 |
266 |
|
389 |
322 |
|
489 |
378 |
| 90 |
126 |
|
190 |
206 |
|
290 |
266 |
|
390 |
322 |
|
490 |
378 |
| 91 |
126 |
|
191 |
206 |
|
291 |
266 |
|
391 |
322 |
|
491 |
380 |
| 92 |
126 |
|
192 |
206 |
|
292 |
266 |
|
392 |
322 |
|
492 |
380 |
| 93 |
128 |
|
193 |
208 |
|
293 |
266 |
|
393 |
326 |
|
493 |
380 |
| 94 |
128 |
|
194 |
208 |
|
294 |
266 |
|
394 |
328 |
|
494 |
380 |
| 95 |
128 |
|
195 |
208 |
|
295 |
270 |
|
395 |
330 |
|
495 |
380 |
| 96 |
128 |
|
196 |
208 |
|
296 |
272 |
|
396 |
330 |
|
496 |
380 |
| 97 |
130 |
|
197 |
210 |
|
297 |
274 |
|
397 |
332 |
|
497 |
380 |
| 98 |
130 |
|
198 |
210 |
|
298 |
274 |
|
398 |
332 |
|
498 |
382 |
| 99 |
130 |
|
199 |
210 |
|
299 |
276 |
|
399 |
334 |
|
499 |
382 |
| 100 |
130 |
|
200 |
210 |
|
300 |
276 |
|
400 |
334 |
|
500 |
382 |
(コメント) 大変感動しました。FNさんに感謝します。
mita さんからのコメントです。(平成22年10月29日付け)
ちょうど、一般の n 個の場合の表面積の最小値はどうなるかを、一般形の式で表すこと
が出来ないか考えていました。
(0)については、私が出題した問題(1)の64個の場合を考えてみると、
直方体において、abc=64 のとき、 2(ab+bc+ca) の最小値を求めよ
という問題に帰着できる(直方体でない形で最小値があるかも知れないという危惧はある
が...(らすかるさん))ので、相加平均と相乗平均の関係より、
2(ab+bc+ca)≧6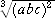 =96
=96
で考えると、最小値が 96 でそのとき、 a=b=c=4 となります。
よって、一般化しても、n=k3 のとき、1辺が k の立方体のとき最小と言えると思います。
(1)と(2)については、 x3=n を満たす実数 x (x は整数でなくても良い)を考えたとき、
x の小数部分が、0.5 より大きいときは、 k(k+1)2
x の小数部分が、0.5 より小さいときは、 k2(k+1)
となりそうです。(根拠はないです。3乗根が計算できることが必要となりますが…)
12×12×14 のケースは見落としてましたが、基本的に、3辺を a、b、c としたときに、
| a−b |+| b−c |+| c−a |≦2
であれば最小になる可能性が高いと言えそうです。
例えば、2002=11×13×14個のケースでも計算しましたが、12×13×13−26 と
した方が、結局、表面積は最小に出来ました。
多少削っても値が変わらなかったりするので一般化は難しいですが、アルゴリズムはまと
められるかもしれません。
基本的な考え方はFNさんが全部説明していただいたので、以下の3つが常に成り立つか
を考えたいと思います。
(0) n=k3 の場合 1辺が k の立方体のとき、最小
(1) n=k2(k+1) の場合 3辺が k、k、k+1 の直方体のとき、最小
(2) n=k(k+1)2 の場合 3辺が k、k+1、k+1 の直方体のとき、最小
厳密な証明ではないのですが、考え方を示してみました。
(0)(立方数)については、前に述べたとおり(相加相乗)とします。
(1)について、n=k2(k+1) とする。このとき、n=k2(k+1)<(k+1)3 である。
m=(k+1)3 とおく。m は立方数なので、このとき、1辺が k+1 の立方体を考える。
このとき、(0)により、1辺が k+1 のき、表面積が最小になる。
ここで、m から、いくつかの1辺が1の立方体を取り除き、個数を n にした時、表面積の
最小が k、k、k+1 の直方体であることを示す。
まず、任意の立体から1つの立方体をとる場合、とることの出来る立体のパターンは、
a: 1つの面が他の立方体に接している → 1つ取ると表面積が4減る
b: 2つの面が他の立方体に接している → 1つ取ると表面積が2減る
c: 3つの面が他の立方体に接している → 1つ取っても表面積は変わらない
d: 4つの面が他の立方体に接している → 1つ取ると表面積が2増える
e: 5つの面が他の立方体に接している → 1つ取ると表面積が4増える
の5パターンが考えられる。
今、1辺が k+1 の立方体から、1つ取ることの出来るパターンは、c、d、e
のどれかしか
ない。
ここで、d、e は明らかに表面積が増えるので、表面積が変わらない c のパターンで取る。
同様に、c のパターンで1列に取り続けるとちょうど k 個取ったときに、b
のパターンで取る
ことの出来る立方体が1つ出来る。
はじめの状態からこの時点まで表面積が変わっていないので、この取り方が表面積が最
小であるといえる。
ここで、k+1 個目に、b のパターンで取ると、全体の表面積が2減る。ここで、FNさんとら
すかるさんが言及していた渦巻き型の取り方で(ただし順番は外側からの逆向きになる)表
面積を最小に保ったまま(取り除く方向を90度変えるごとに、b のパターンで取り、表面積
を減らせる。)
最後に、(k+1)2個を取るときに、a のパターンでとり、表面積を最小に出来る。これで、
(2)の状態になったので、
(2) n=k(k+1)2 の場合 3辺が k、k+1、k+1 の直方体のとき、最小
といえる。
(注意:他の面に移ってこのパターンで取ると、(k+1)2個目に取るときに、a のパターン
で取ることが出来ないのでこの方法が最小と言える。)
ここで、n=k(k+1)2 の状態から、(1)の n=k2(k+1) の状態にするには、
あと、k(k+1)個取らなくてはいけない。このとき、(k+1)2の面で先ほどのとり方を行うと
k+1個残ってしまい表面積が余分に発生する。
よって、残った面のk(k+1)の形をした面で先ほどと同じように取っていくと、結果的に3
辺が k、k、k+1 の直方体のとき最小 といえる。
よって(1)の場合も表面積が最小といえる。
(コメント) FNさん、らすかるさん、mita さんに感謝します。
らすかるさんが、「与えられた自然数 n から最小表面積を求める式」を作られました。
(平成22年10月30日付け)
与えられた自然数 n に対して、n 個の立方体(1個の立方体の1辺の長さは1)で出来る
立体の表面積の最小値 S は、
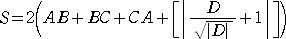
で与えられる。ただし、
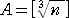
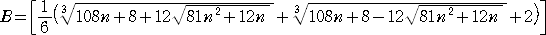
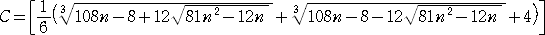
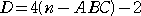
(注意) | |は絶対値、[ ]はガウス記号
プログラムで計算する時は、[ ]で切り捨てる時、丸め誤差によって整数よりわずかに
小さい値になっている可能性に注意して下さい。
例 n=300 の場合に、上記の式を適用してみた。
A=[6.69433・・・ ]=6
B=[(40.16928・・・+0.099579・・・+2)/6 ]=[7.0448・・・ ]=7
C=[(40.16267・・・+0.099595・・・+4)/6 ]=[7.37704・・・ ]=7
D=4(300−6×7×7)−2=22
より、 S=2(6×7+7×7+7×6+[4.690416・・・+1])
=2(42+49+42+5)
=276
(コメント) イヤ〜、これは感動的ですね!上式の発見そのものが不思議です...。
らすかるさんによれば、FNさんの作られたM(N)と n=10万まで値が一致することは確
認されたそうである。(平成22年10月30日付け)
式は複雑ですが、結局、M(N)でやっていることと大して変わりません。
k3 、k2(k+1) 、k(k+1)2 を考えると、
n=A×B×C
1=1×1×1
2=1×1×2
4=1×2×2
8=2×2×2
12=2×2×3
18=2×3×3
27=3×3×3
36=3×3×4
48=3×4×4
64=4×4×4
・・・・・・
のようになりますので、
Aは、 k3≦n<(k+1)3 となる k、つまり、 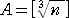
Bは、 (k−1)k2≦n<k(k+1)2 となる k、つまり、3次方程式 (k−1)k2=n を解いて
ガウス記号を付けたものが、
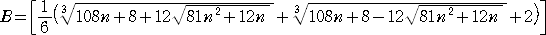
Cは、 (k−1)2k≦n<k2(k+1) となる k(Bと同様)、つまり、
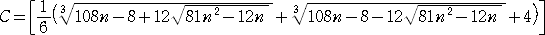
そして、n−ABC は「直前の直方体に追加した立方体の個数」であり、2[|D/√|D|+1|]
は
立方体を k 個追加した時に増える表面積の
0、4、6、8、8、10、10、12、12、12、14、14、14、16、16、16、16、18、・・・
が得られる式を適当に考えたものです。
1個以上の追加に限れば、表面積の増加分は、2[√D+1] で得られますが、0個の時に
0が得られるように少し変形したものです。
「0個」の特別扱いが必要で追加分の式が少し面倒になっていますが、「0個」を「1個前の
直方体に立方体を追加したもの」と考えれば、式が少し簡単になるかも知れません。
(コメント) らすかるさん、公式の説明、ありがとうございます。
以下工事中







