2次形式 
線形代数学で行列の標準化を学んだ後の応用例として「2次形式の理論」が講義や書籍
等で扱われる。手頃な演習問題だからだろう。
ここでは、2変数の場合について、2次形式の理論をおさらいしておこう。
2次の実対称行列
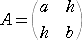
を用いて、 F( x , y )=txAx (ただし、tx=( x y ) )
で与えられる整式 F( x , y )を、変数 x 、y についての2次形式という。
このとき、2次形式 F( x , y ) は、 F( x , y )=ax2+2hxy+by2 と書ける。すなわ
ち、整式 F( x , y ) は、2次の項ばかりからなっている。
2次形式の理論においては、この式を、 F( x , y )=A[x] と書き表すようだ。
係数行列 A が実対称行列であることから、直交行列 P により対角化される。
よって、次の定理が成り立つ。
定 理 2次形式 F( x , y )=A[x] に対し、適当な直交変換 y=Px (tP=P-1)を
行うことにより、
A[y]=(P-1AP)[x]=λx2+μy2
となる。ここで、λ、μ は、行列 A の固有値である。
例 F( x , y )=3x2−2xy+3y2 のとき、
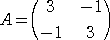
に対して、 det(A−kE)=k2−6k+8=(k−2)(k−4)=0 より、 k=2、4
| このとき、(A−2E)(A−4E)= |
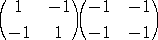 |
=0 (但し、Eは単位行列) |
(A−2E)(A−4E)=(A−2E)(u v) (ただし、u、v は、A−4E の列ベクトル)
右辺を計算して、 (A−2E)(A−4E)=(A−2E)(u v)=((A−2E)u (A−2E)v)= 0
なので、 (A−2E)u=0 となり、 A−4E の列ベクトル u が、固有値 2 に属する
固有ベクトルになることが分かる。固有値 4 に属する固有ベクトルの求め方も同様。
(→ 参考:「固有ベクトルを求める」)
| したがって、、k=2に属する固有ベクトル(の一つ)は、 |
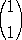 |
| k=4に属する固有ベクトル(の一つ)は、 |
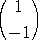 |
よって、直交行列
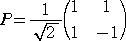
により、
(P-1AP)[x]=2x2+4y2
と書ける。
上記の例において、
少なくとも一つが 0 でない実数 x , y が何であっても、 F( x , y
)>0
であることが分かる。それは、x2、y2 の係数である固有値 2 と 4 が正の数であることか
ら明らかだろう。
一般に、全ての x≠0 に対して、A[x]>0 のとき、A[x] および対称行列 A は正値
であると言われる。
同様に、全ての x≠0 に対して、A[x]≧0 のとき、A[x] および対称行列 A は半正値
であると言われる。
一般に次の事実が知られている。
定 理 2次形式 F( x , y )=A[x] が正値であるための必要十分条件は、実対称行
列 A の固有値が全て正であることである。
証明は明らかだろう。
平成21年6月20日付けで、以前お世話になった「文系大学生」様より、当HPの掲示板
「出会いの泉」に書き込みがあった。
行列の2次形式の符号についての質問です。
2つの実対称行列 A、B について、2次形式をそれぞれ、
G( x , y )=A[x] 、 H( x , y )=B[x]
とする。
さらに、実対称行列 A+B に対して、2次形式
F( x , y )=(A+B)[x]=G( x , y )+H( x , y )
を定める。
このとき、 F( x , y ) の符号を定めるとき、
G( x , y )>0 かつ H( x , y )>0 ならば、F(
x , y )>0
G( x , y )<0 かつ H( x , y )<0 ならば、F(
x , y )<0
としてもいいのだろうか?
一見これでいいのかなと思ったのですが、G( x , y ) をさらに、
G1( x , y )=( 0 b )[x] 、 G2( x , y )=( a 0 )[x]
としてやると、G1( x , y )とG2( x , y )の行列の行列式が、0 となってしまう。
ということは、H( x , y )についても同じようにしてやると、F( x
, y )が 0 になってしまう?
でも、F( x , y )から出てきたものだし...と混乱して、これらの関係が整理できませんで
した。
(コメント) 途中までは、「うん、そうだね!」と思い読んでいましたが、最後のところが「?」
でした。2次形式というと、係数行列が対称行列と相場が決まっていますが、列で
分解した行列では対称行列でなくなるので2次形式とは呼べないのでは...?
ですから、固有値がどうのこうのとか、行列式がどうのこうのとかは意味をなさな
くなるのでは...?文系大学生様、私の勘違いだったら、ご容赦を...。
