３．２次体の整数　　　 　 　　　　　　　　　　　　　

　平成１７年の私自身の積み残しの問題として、

　　　ｙ³＝ｘ²−１　を満たす自然数解は、（ｘ，ｙ）＝（３，２）　のみ

というものがある。この問題は、平成１７年６月２日にＨＮ「通り人」さんが出題されたもので
ある。これに対して、当ＨＰがいつもお世話になっているＨＮ「らすかる」さんが、「Thue方程
式」の問題に翻訳して、プログラムにより解決された。（平成１７年６月５日付け）

　　右辺を因数分解すると、　y³＝(ｘ＋１)(ｘ−１)　である。連続する正の奇数の積は三乗数
にならないので、ｘは奇数に限る。

　ｘが奇数(ｘ≧３)、ｙが偶数(ｙ≧２)なので、　　　　ｘ＝２ｍ＋１、ｙ＝２ｎ　（ｍ、ｎ≧１）
　とおくと、　４ｍ（ｍ＋１）＝８ｎ³　となり、　ｍ（ｍ＋１）＝２ｎ³

　　ｍが偶数のとき、　ｍ＝２ｋ　（ｋ≧１）とおくと、　　　　　ｋ（２ｋ＋１）＝ｎ³
　ｋ と ２ｋ＋１ は互いに素なので、両方とも三乗数でなければならない。
　そこで、　ｋ＝ｔ³（ｔ≧１）、２ｋ＋１＝ｓ³　（ｓ≧１）とおくと、　　　２ｔ³＋１＝ｓ³
　となる。

　同様にして、

　　ｍが奇数のとき、　ｍ＝２ｋ−１　（ｋ≧１）とおくと、　　　ｋ（２ｋ−１）＝ｎ³
　ｋ と ２ｋ−１ は互いに素なので、両方とも三乗数でなければならない。
　そこで、　ｋ＝ｔ³（ｔ≧１）、２ｋ−１＝ｓ³　（ｓ≧１）とおくと、　　　２ｔ³−１＝ｓ³
　となる。

　したがって、２ｔ³±１＝ｓ³ （Thue方程式）を解けば良いことになる。

　このとき、　ｐａｒｉ/ｇｐ というプログラムで

　　th=thueinit(x^3-2)
　　thue(th,1)
　　thue(th,-1)

　と入力するだけで、(ｓ,ｔ)＝±(１,０),±(１,１)という全解が得られる。
　問題の条件より、(ｓ,ｔ)＝(１,１) で、このとき、　ｋ＝１
　よって、ｍ＝ｎ＝１ となり、自然数解は　（ｘ,ｙ)＝(３,２)　のみ。


　らすかるさんによれば、「手計算で簡単に解けるような問題ではない」ということである。

　北海道大学の中村先生に、この問題について伺ったところ、らすかるさんと同じく、「簡
単な計算ではできない」とのことである。

　ｙ³＝ｘ²−１ を　ｙ³＋１＝ｘ²　と変形し、１の３乗根ωを用いて、(ｙ＋１)(ｙ＋ω)(ｙ＋ω²)＝ｘ²
と因数分解。このとき、Ｑ(ω)での素数の分解法則やＺ［ω］の単項イデアル整域という性質
を用いて証明できるだろう

との助言を頂いた。

　このページでは、中村先生からの指針を参考にしながら、冒頭の問題解決のための理
論的な知識を整理していきたいと思う。

　表題の「２次体」の「体」は、数学における「群・環・体」の「体」のことである。これは、あま
り難しく考える必要はなく、我々が通常計算している世界が、「体」の世界である。簡単に言
えば、「体」とは、四則演算が自由にできる数の集合のことを言う。

例（有理数体 Ｑ）　有理数の集合で、演算（＋−×÷）が可能である。

例（実数体 Ｒ）　実数の集合で、演算（＋−×÷）が可能である。（→中学で学習）

例（複素数体 Ｃ）　複素数の集合で、演算（＋−×÷）が可能である。（→高校で学習）

　上記の３つの数体には、　Ｑ　⊂　Ｒ　⊂　Ｃ　という関係がある。

このような関係があるとき、Ｑ は Ｒ の部分体、Ｒ は Ｃ の部分体であるという。


　整数論の基礎知識 において、ガウスの整数のいろいろな性質を考察した。

　（ガウスの整数）　 　ａ＋ｂ・ｉ　　　（ａ、ｂ は有理整数　、ｉ は虚数単位）

　この整数は、和・差・積の演算について閉じているが、商については閉じていない。

したがって、ガウスの整数の集合は、体にはならない。

　そこで、ｉ を虚数単位として、複素数　ａ＋ｂ・ｉ　　　（ａ、ｂ は有理数）の集合を考える。

この集合は、通常　Ｑ（ｉ）　で表される。

ここでは四則演算が自由にできるので体となる。　Ｑ（ｉ） をガウスの数体と言う。

Ｑ（ｉ） は、虚２次体である。これに対して、Ｑ（）などは実２次体と言われる。

α＝ａ＋ｂ・ｉ　を解に持つ２次方程式は、

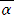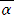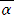　　　　（Ｘ−α)(Ｘ−）＝Ｘ²−（α＋）Ｘ＋α・＝０

で与えられる。　このとき、係数はすべて有理数である。

　多項式　（Ｘ−α)(Ｘ−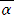） のことを、　α の主多項式という。

　さて、冒頭の問題解決のためには、まず、虚２次体 Ｑ(ω) について、その性質を調べる
必要がありそうだ。

　ω は、１の３乗根で、２次方程式 Ｘ²＋Ｘ＋１＝０　の解である。解の公式から、

　　　　　　　　　　　　

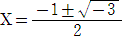
である。
　　　　　　　　　　　　
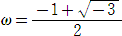
とおくと、
　　　　　　　　　　　　
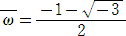
である。

　明らかに、　ω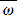＋＝−１　、　ω・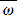＝１　　が成り立つ。

また、　ω²＋ω＋１＝０　であることから、　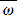＝ω²　である。


　ａ＋ｂ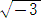　（ａ、ｂ は有理数）の集合からなる体を考えるので、通常は、Ｑ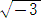（）とす
るところだが、実は、Ｑ(ω) を用いる理由がある。

　Ｑ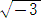（）における整数は、実は、

　　　　　　　　ａ＋ｂ・ω　　　（ａ、ｂ は有理整数）

の形に限定されるらしい。そういうこともあって、Ｑ(ω) を用いることが納得される。

　α＝ａ＋ｂ・ω　（ａ、ｂ は有理数）に対して、その共役を　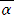＝ａ＋ｂ・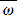　と定義する。

このとき、α＝ａ＋ｂ・ω　のノルム（Norm）を

　　　　　　Ｎ（ａ＋ｂ・ω）＝（ａ＋ｂ・ω）・（ａ＋ｂ・）＝ａ²−ａｂ＋ｂ²

と定義する。明らかに、ノルムの値は、０ 以上の有理数である。

　ノルムについて、次の性質が成り立つ。（証明は、明らかだろう。）

　　　Ｎ（α・β）＝Ｎ（α）・Ｎ（β）　　、　　　Ｎ（α/β）＝Ｎ（α）/Ｎ（β）

　ノルムと同様にして、シュプール（Ｓｐｕｒ）（または、トレース（trace））が定義される。

　　　　　　Ｓ（ａ＋ｂ・ω）＝（ａ＋ｂ・ω）＋（ａ＋ｂ・）＝２ａ−ｂ

　シュプールについて、次の性質が成り立つ。（証明は、明らかだろう。）

　　　　　　Ｓ（α＋β）＝Ｓ（α）＋Ｓ（β）

　明らかに、シュプールの値は、０ 以上の有理数である。

例　　α＝５＋８ω　のノルム　Ｎ（α）＝５²−５・８＋８²＝２５−４０＋６４＝４９
　　　　　　　　　　シュプール　Ｓ（α）＝２・５−８＝１０−８＝２


　α＝ａ＋ｂ・ω　に対して、そのノルムとシュプールは、どんな幾何学的意味があるのだろう
か？下図を、ボーっと眺めていると、その意味がよく分かる。

　　　　　　　　

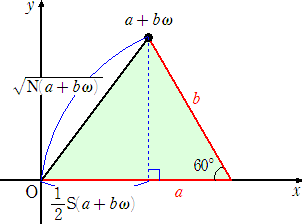
　Ｎ（ａ＋ｂ・ω）は、２辺の長さが ａ、ｂ で、その間の角が６０°の三角形で、その角の対辺
の長さの平方である。

　Ｓ（ａ＋ｂ・ω）は、２辺の長さが ａ、ｂ で、その間の角が６０°の三角形で、第３辺のａ方向
の正射影の長さの２倍である。

　Ｑ(ω) において、　ａ＋ｂ・ω　（ａ、ｂ は有理整数）　の形の数を「整数」と定義する。

　全ての整数の約数となる整数を、単数という。単数は、有理整数 １ と同じ働きを持つ。

　Ｑ( ｉ ) において、単数は、　１　、−１　、　ｉ　、　−ｉ　の４個であった。それでは、Ｑ(ω) に
おいて、単数とは、どのようなものであろうか。実際に、求めてみよう。

　単数の性質から、　Ｎ（ａ＋ｂ・ω）＝１　が成り立つので、　　ａ²−ａｂ＋ｂ²＝１

　ａ の２次方程式　ａ²−ａｂ＋ｂ²−１＝０　において実数解を持つので、判別式をＤとすると、

　Ｄ＝ｂ²−４（ｂ²−１）＝４−３ｂ²≧０　となる。　ｂ は整数なので、　ｂ＝０、１、−１

　　　　　ｂ＝０　のとき、　ａ²＝１　より、　ａ＝１、−１

　　　　　ｂ＝１　のとき、　ａ²−ａ＝０　より、　ａ＝０、１

　　　　　ｂ＝−１　のとき、　ａ²＋ａ＝０　より、　ａ＝０、−１

　従って、求める単数は、次の６個である。

　　　　　　　　　１　、−１　、ω　、−ω　、　１＋ω　、−１−ω

　ここで、　１＋ω＝−ω²　なので、単数として、

　　　　　　　　　１　、−１　、ω　、−ω　、　ω²　、−ω²

としてもよい。また、次の性質も面白い。

　Ｑ(ω) において、整数のノルムは、３以上である。

したがって、ノルムが２となる整数は存在しない。

　実際に、もし存在したとすると、ａ²−ａｂ＋ｂ²＝２　であるが、判別式をＤとすると、

　Ｄ＝ｂ²−４（ｂ²−２）＝８−３ｂ²≧０　となる。　ｂ は整数なので、　ｂ＝０、±１、±２

　　　　　ｂ＝０　のとき、　ａ²＝２　より、　ａ は整数とならない。

　　　　　ｂ＝１　のとき、　ａ²−ａ−１＝０　より、　ａ は整数とならない。

　　　　　ｂ＝−１　のとき、　ａ²＋ａ−１＝０　より、　ａ は整数とならない。

　　　　　ｂ＝２　のとき、　ａ²−２ａ＋２＝０　より、　ａ は整数とならない。

　　　　　ｂ＝−２　のとき、　ａ²＋２ａ＋２＝０　より、　ａ は整数とならない。

　以上から、ａ²−ａｂ＋ｂ²＝２　を満たす整数解は存在しない。


　整数 α に対して、単数および、 α に単数を乗じたものは、自明な約数で、有理整数にお
ける、１と−１ と同様に因数としては、度外視して考えるものとする。

例　６＝１・６　とは普通考えない。　６＝２・３　と因数に分解する方が自然であろう。

　整数 α に対して、自明でない約数を、真の約数という。

　このとき、整数 α が、０ でも単数でもなく、かつ、真の約数を持たないとき、素数であると
いう。

例　Ｑ(ω) において、　１＋２ω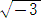＝　は素数である。
　　実際に、Ｎ（１＋２ω）＝３　で、整数のノルムは３以上であるから、１＋２ω　は真の約数
　を持ち得ない。
　　このことから、３ は、Ｑ(ω) において素数でないことも分かる。

　整数 α に対して、素数 ｐ 、ｑ 、・・・　があって、　α＝ｐ×ｑ×・・・　と積の形にかけるとき、
整数 α は、素因数に分解されるという。

　これまでの話から、整数 α が有限個の素因数に必ず分解できるということは理解できる
だろう。しかし、素因数分解において、大切なことは、その分解の一意性にある。もし、一意
性が成立すれば、有理整数における性質が、Ｑ(ω) の整数においても同様に成り立つこと
になる。

　Ｑ(ω) においても、素因数分解の一意性が成り立つ。

　このことを確認するには、まず次の定理（整除の定理）が必要だ。

定理　　任意の整数 α 、β （β≠０） に対して、

　　　　　　　　　α ＝ β・ｑ＋ｒ　　（　Ｎ（ｒ）＜Ｎ（β） ）

　　　　を満たす整数 ｑ 、ｒ が存在する。

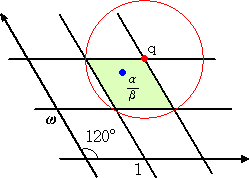（証明）　ガウス平面（複素数平面）において、明らか 　　　　に、ある整数 ｑ が存在して、Ｎ（α/β−ｑ）＜１ 　　　　とできる。そこで、　ｒ＝α−β・ｑ　とおくと、ｒ は 　　　　整数で、 　　　Ｎ（ｒ）＝Ｎ（α−β・ｑ）＝Ｎ（β・（α/β−ｑ）） 　　　　　　　　　　　　　　＝Ｎ（β）・Ｎ（α/β−ｑ）＜Ｎ（β） 　　以上から、　α ＝ β・ｑ＋ｒ　（　Ｎ（ｒ）＜Ｎ（β） ）　を 　満たす整数 ｑ 、ｒ が存在する。（証終）

　この定理により、Ｑ(ω) の整数においても、ユークリッドの互除法を行うことができる。

　従って、ガウスの整数と同様の議論により、Ｑ(ω) においても素因数分解の一意性が成
り立つ。

　さて、上記の例で、「 Ｑ(ω) において、整数　１＋２ω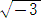＝　は素数である」ことを述べ
た。それでは、 Ｑ(ω) における素数として他にどんなものがあるのだろうか？

　いま、整数 α を素数として、 α で割り切れる正の有理整数のうちで最小のものを、ｐ　と
する。このような ｐ は必ず存在する。（例えば、Ｎ（α）は、α で割り切れる。）

　このとき、　ｐ は、有理素数である。

　実際に、　α は素数で単数ではないから、ｐ ≧ ３ で、ｐ が有理素数でないとすると、
　　　　　　　　　　　　　ｐ ＝ ｘ・ｙ　（ ｐ＞ｘ＞１ 、ｐ＞ｙ＞１ ）
　　　　　　　となる有理整数 ｘ 、ｙ が存在し、ｘ または ｙ は、α で割り切れる。
　　　　　　　これは、ｐ の最小性に矛盾する。　よって、　ｐ は、有理素数である。

　したがって、素数 α は、有理素数 ｐ の約数となる。そこで、　ｐ ＝ α・β　とおける。

このとき、　Ｎ（ｐ）＝Ｎ（α）・Ｎ（β）　で、Ｎ（ｐ）＝ｐ²　なので、

　　　　　　　Ｎ（α）＝ｐ　　または　　Ｎ（α）＝ｐ²

となる。

　Ｎ（α）＝ｐ　のとき、　ｐ＝α・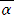　で、これは、ｐ の素因数分解となるので、有理素数 ｐ は

Ｑ(ω) における素数とはなり得ない。　（例　３＝（１＋２ω)(１＋２）　）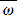

　Ｎ（α）＝ｐ² のとき、　Ｎ（β）＝１ で、β は単数で、α は、ｐ と同伴数となる。

　このとき、ｐ は、Ｑ(ω) においても素数となる。

　したがって、有理素数 ｐ を与えたとき、

　　ａ²−ａｂ＋ｂ²＝ｐ　が有理整数解 ａ、ｂ を持てば、　α＝ａ＋ｂ・ω　は素数

　　ａ²−ａｂ＋ｂ²＝ｐ　が有理整数解 ａ、ｂ を持たなければ、　ｐ そのものが素数

であることが分かった。

例　有理素数の ３ は、Ｑ(ω) においては素数となりえない。

　実際に、　ａ²−ａｂ＋ｂ²＝３　において有理整数解 ａ、ｂ が存在するとすれば、

判別式 Ｄ ＝ｂ²−４（ｂ²−３）＝１２−３ｂ²≧０　より、　ｂ＝０、±１、±２

　　ｂ＝０　のとき、　ａ²＝３　となり、　ａ は整数とならない。

　　ｂ＝１　のとき、　ａ²−ａ−２＝０　となり、　(ａ−２)(ａ＋１)＝０　より、　ａ＝２、−１

　　　　よって、　２＋ω　、−１＋ω　は、素数である。

　　ｂ＝−１　のとき、　ａ²＋ａ−２＝０　となり、　(ａ＋２)(ａ−１)＝０　より、　ａ＝−２、１

　　　　よって、　−２−ω　、１−ω　は、素数である。

　　ｂ＝２　のとき、　ａ²−２ａ＋１＝０　となり、　(ａ−１)²＝０　より、　ａ＝１

　　　　よって、　１＋２ω　は、素数である。

　　ｂ＝−２　のとき、　ａ²＋２ａ＋１＝０　となり、　(ａ＋１)²＝０　より、　ａ＝−１

　　　　よって、　−１−２ω　は、素数である。

　以上から、ａ²−ａｂ＋ｂ²＝３　は、有理整数解 ａ、ｂ をもつので、有理素数の ３ は、Ｑ(ω)
においては素数となりえない。


　この６個の素数（２＋ω、−１＋ω、−２−ω、１−ω、１＋２ω、−１−２ω）は互いに同伴数
である。

　実際に、１＋ω＝−ω²、ω³＝１　で、単数 １、−１、ω、−ω、１＋ω、−１−ω を用いて、

　　　　−１＋ω＝（２＋ω）ω　、−２−ω＝（２＋ω）（−１）　、１−ω＝（２＋ω）（−ω）
　　　　１＋２ω＝（２＋ω）（１＋ω）　、−１−２ω＝（２＋ω）（−１−ω）

と書けることから明らかであろう。


例　有理素数の ５ は、Ｑ(ω) においても素数である。

　実際に、　ａ²−ａｂ＋ｂ²＝５　において有理整数解 ａ、ｂ が存在するとすれば、

判別式 Ｄ ＝ｂ²−４（ｂ²−５）＝２０−３ｂ²≧０　より、　ｂ＝０、±１、±２

　　ｂ＝０　のとき、　ａ²＝５　となり、　ａ は有理整数とならない。これは、矛盾。

　　ｂ＝±１　のとき、　ａ²−（±１）ａ−４＝０　となり、　ａ は有理整数とならない。これは、矛盾。

　　ｂ＝±２　のとき、　ａ²−（±２）ａ−１＝０　となり、　ａ は有理整数とならない。これは、矛盾。

　以上から、ａ²−ａｂ＋ｂ²＝５　は、有理整数解 ａ、ｂ をもたないので、有理素数の ５ は、
Ｑ(ω) においても素数となる。

　実は、有理素数 ｐ が、Ｑ(ω) において、素数になるかどうかについては、次の定理が知ら
れている。

定理　　２次体 Ｑ(ω) において、有理素数 ｐ は、

　　　　ｐ ≡ １　（ｍｏｄ　３）　のとき、　素数にならない

　　　　ｐ ≡ ２　（ｍｏｄ　３）　のとき、　素数になる

　この定理によれば、有理素数の５は素数で、７は素数にはならないことが分かる。そして、

　　±（３＋ω）、±（−２＋ω）、±（３＋２ω）、±（−１＋２ω）、±（１＋３ω）、±（２＋３ω）

が互いに同伴な素数であることも分かる。

　さて、Ｌｅｇｅｎｄｒｅ の記号 （ａ/ｐ） を用いて、上記の定理を証明してみよう。

（証明）　ａ²−ａｂ＋ｂ²＝ｐ　を満たす有理整数解 ａ、ｂ が存在するとする。

　　　このとき、　４ｐ＝４ａ²−４ａｂ＋４ｂ²＝（２ａ−ｂ）²＋３ｂ²　と書ける。

　　　よって、　（２ａ−ｂ）²≡ｐ　（ｍｏｄ　３）　なので、　（ｐ/３）＝１ となる。

　　　Ｅｕｌｅｒ の規準より、　（ｐ/３）≡ｐ　（ｍｏｄ　３）　なので、　ｐ≡１　（ｍｏｄ　３）　となる。

　　　逆に、　ｐ≡１　（ｍｏｄ　３）　とする。このとき、明らかに、（ｐ/３）＝１ である。

　　　平方剰余の相互法則より、　（ｐ/３）（３/ｐ）＝（−１）^{（ｐ−1）/2・（3−1）/2}＝（−１）^{（ｐ−1）/2}

　　　なので、　　　（３/ｐ）＝（−１）^{（ｐ−1）/2}　　である。

　　　よって、　ｐ は奇素数なので、

　　　　（−３/ｐ）＝(−１/ｐ)(−３/ｐ)＝（−１）^{（ｐ−1）/2}・（−１）^{（ｐ−1）/2}＝（−１）^{（ｐ−1）}＝１

　　　すなわち、　方程式 Ｘ²≡−３　（ｍｏｄ　ｐ）　は有理整数解 ｍ を持つ。

　　　このとき、　ｐ と　ｍ−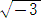　の最大公約数を　Ｍ とすると、

　　　　　　Ｍ＝　１　または　Ｍ＝　ｐ　または　Ｍ＝ α　（ ｐ＝α・　)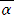

　　　の何れかになるが、ｍ−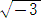 は、ｐ で割り切れないので、Ｍ＝　ｐ　は起こりえない。

　　　また、Ｍ＝　１　とすると、　ｐ は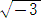、　ｍ−　、ｍ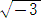＋　と互いに素になる。

　　　　　　　すなわち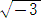､　（ｍ−)(ｍ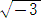＋）＝ｍ²＋３　と ｐ は互いに素となる。

　　　　　　　これは、ｍ²≡−３　（ｍｏｄ　ｐ）　に矛盾する。

　　　よって、　Ｍ＝　α　（ ｐ＝α・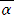　)　の場合しか起こらない。

　　　以上から、　ａ²−ａｂ＋ｂ²＝ｐ　を満たす有理整数解 ａ、ｂ が存在する。（証終）

（コメント）　厳密な証明は難しいので、雰囲気を味わうだけ．．．。

　以上で、２次体（虚２次体） Ｑ（ｉ）、Ｑ(ω) のもつ性質をいろいろ見てきた。これらは何れ
も単数の個数は有限で、かつ、素因数分解の一意性が有理整数同様保たれている。

　しかし、２次体の中には、単数が無限個あったり、素因数分解の一意性が成り立たないも
のもある。

　　　単数が無限個ある２次体の例　・・・・・　Ｑ（）
　　　素因数分解の一意性が成り立たない２次体の例　・・・・・　Ｑ（）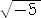

　一般論に入る前に、それらの２次体の構造を探訪することにしよう。

　Ｑ（）における整数は、　α ＝ ａ＋ｂ　（ａ、ｂ は有理整数）の形をしている。

α ＝ ａ＋ｂ　に対して、その共役は、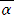 ＝ ａ−ｂ　である。

　このとき、　α のノルム　Ｎ（α）＝α・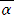＝ａ²−２ｂ²
　　　　　　　　　シュプール　Ｓ（α）＝α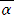＋＝２ａ
である。

例　α ＝ １＋　について、Ｎ（α）、Ｓ（α）を求めてみよう。

　　　　　Ｎ（α）＝（１＋）（１−）＝１−２＝−１
　　　　　Ｓ（α）＝１＋＋１−＝２

　この例からも分かるように、Ｑ（）の世界では、

　　　　　Ｎ（α）＜０　　、　　Ｎ（α）≠｜α｜²

という場合も起こりうる。　これは、Ｑ（ｉ）、Ｑ(ω) ではなかった性質である。

　今、　α ＝ ａ＋ｂ　を単数とすると、α は、１の約数なので、１＝α・α’　となる整数 α’が
存在する。

　よって、　Ｎ（１）＝Ｎ（α・α’）＝Ｎ（α）・Ｎ（α’）　で、Ｎ（１）＝１　より、　Ｎ（α）＝１、−１

　　　　　　すなわち、　ａ²−２ｂ²＝１　、　ａ²−２ｂ²＝−１

これらを解くと、　（ ａ ， ｂ ）＝（ ±１ ， ０ ）、（ １ ， １ ）

　このとき、　１ 、 −１ 、 １＋　が単数となるが、　α’＝１/α＝−１＋　も単数である。

また、　１＝α・α’　より、　１＝α^ｎ・α’^ｎ　なので、　α^ｎ も単数となる。

　このことから、　Ｑ（）において、単数は無限個あることが理解される。

　Ｑ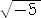（）における整数は、　α ＝ ａ＋ｂ　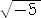（ａ、ｂ は有理整数）の形をしている。

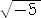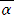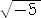α ＝ ａ＋ｂ　に対して、その共役は、 ＝ ａ−ｂ　である。

　このとき、　α のノルム　Ｎ（α）＝α・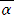＝ａ²＋５ｂ²
　　　　　　　　　シュプール　Ｓ（α）＝α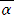＋＝２ａ
である。

　今、　α ＝ ａ＋ｂ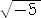　を単数とすると、α は、１の約数なので、１＝α・α’　となる整数 α’
が存在する。

　よって、　Ｎ（１）＝Ｎ（α・α’）＝Ｎ（α）・Ｎ（α’）　で、Ｎ（１）＝１　より、　Ｎ（α）＝１

　　　　　　すなわち、　ａ²＋５ｂ²＝１

この解は、　（ ａ ， ｂ ）＝（ ±１ ， ０ ）　のみである。

　よって、　Ｑ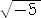（）における単数は、　１ 、 −１ 　の２つである。

　一般に、Ｑ（ｉ）、Ｑ(ω) 以外の虚２次体において、単数は、１ 、 −１ 　の２つしか存在しな
いことが知られている。

　Ｑ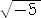（）において、素因数分解の一意性が成り立たないことは、次の例から明らかだ
ろう。

例　　６＝２・３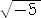＝（１＋）（１−）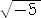

（コメント）　これを書いていると、院試で整数論の土井先生から、「素因数分解の一意性が
　　　　　　成り立たない例をあげてください。」と質問されたことが突然思い出された。


　H．Nakao さんからのコメントです。（令和３年１０月２日付け）

　可能であれば、整数環上で、"既約である"と"素である"とが一致しない具体例を挙げて
欲しいです。

　Z(有理整数環)では、nが既約元であることとnが素元であることは同値です(良く知られてい
る)が、2Z(偶数の有理整数のみからなる環、単元を持たないことに注意）では、

　6は2Zで既約元である。(6を２つの偶数の積に分解できないから)

　6は2Zで素元ではない。(36=6*6=2*18より、6は36を割るが、6は2を割らない、かつ、6は
　　　　　　　　　　　　　　　18を割らないから)

となることを、

　Joseph. H. Silverman, "A Friendly Introduction to Number Theory Second Edition",
Prentice Hall Inc., 2001, ISBN0-13-030954-0

を読んた時に、こんな簡単な例があったのかと、衝撃を受けました。これにより、"素"である
ことの重要さが分かりました。



　　以下、工事中