
四面体で、全ての面が合同な鋭角三角形であるとき、等面四面体と言われる。等面四面
体の問題は難関大学で頻出であり、受験生にとっては必ず経験しておいた方がよい分野
である。対処の仕方を知っているかどうかで大きな差がつく問題だからである。
等面四面体は、直方体の8つの頂点のうち、互いに隣り合わない4つの頂点を結んででき
る四面体で、各面が合同な鋭角三角形であると特徴付けられる。
この「等面四面体は直方体に埋め込まれる」という性質を用いた、次の早稲田大学教
育学部(2014)の問題が標準的な問題と言える。
問題 四面体ABCDは4つの面のどれも3辺の長さが 7、8、9 の三角形である。この四
面体ABCDの体積を求めよ。
(解) 題意より、四面体ABCDは直方体AQDR-SCPBに埋め込み可能である。
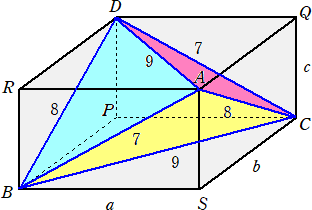
このとき、 a2+b2=81、b2+c2=64、c2+a2=49 が成り立つことから、
2(a2+b2+c2)=194 より、 a2+b2+c2=97
よって、 a2=16 、b2=33 、c2=48 より、 a=4 、b=√33 、c=4
このとき、直方体の体積は、 4×√33×4
三角錐R-ABD、三角錐S-ABC、三角錐Q-ACD、三角錐P-BCDの体積は、
何れも、 4×√33×4
求める四面体ABCDの体積は、 48
読者のために練習問題を残しておこう。
練習問題 四面体ABCDは4つの面のどれも3辺の長さが 5、7、8 の三角形である。この
四面体ABCDに内接する球の半径 r 、外接する球の半径Rを求めよ。
(解) 直方体の3辺の長さを a、b、c とおくと、
a2+b2=49、b2+c2=64、c2+a2=25 が成り立つことから、
2(a2+b2+c2)=138 より、 a2+b2+c2=69
よって、 a2=5 、b2=44 、c2=20 より、 a=
このとき、 四面体ABCDの体積Vは、 V=
3辺の長さが 5、7、8 の三角形の面積Sは、ヘロンの公式より、 S=10
よって、求める r の値は、 (r・S/3)×4=V より、 r=(√33)/2
また、外接する球の半径Rは、 R=(√(a2+b2+c2))/2=(√69)/2 である。 (終)
冒頭の「等面四面体は直方体に埋め込まれる」という性質を問う問題が京都大学で出
題されている。
問題 △ABCは鋭角三角形とする。このとき、各面すべてが△ABCと合同な四面体が存在
することを示せ。
(解) △ABCの3辺の長さを a、b、c とする。このとき、
x2+y2=a2 、y2+z2=b2 、z2+x2=c2
を満たす正の数 x、y、z が存在すれば、所要の四面体が埋め込まれる直方体が得られる。
2(x2+y2+z2)=a2+b2+c2 から、 x2+y2+z2=(a2+b2+c2)/2
よって、 x2=(a2+b2+c2)/2−b2=(a2−b2+c2)/2
△ABCは鋭角三角形なので、 a2−b2+c2>0 より、上の方程式を満たす正の数 x
は存在する。
同様にして、正の数 y、z も存在するので、所要の四面体が存在することが分かる。 (終)
等面四面体では、重心、外心、内心が一致するという性質を持つ。この性質を持つ平面図
形では正三角形が有名である。
2014年度入試では、東京医科歯科大学でも等面四面体の問題が出題されている。
問題 0<θ<π/2 を満たす実数θに対し、xyz空間内の4点 A(cosθ,cosθ,sinθ)、
B(-cosθ,-cosθ,sinθ)、C(cosθ,-cosθ,-sinθ)、D(-cosθ,cosθ,-sinθ) を
頂点とする四面体の体積をV(θ)とする。このとき、以下の各問いに答えよ。
(1) V(π/6)を求めよ。
(2) 0<θ<π/2 におけるV(θ)の最大値を求めよ。
条件から、辺の長さを求めてみると、
AB2=4cos2θ+4cos2θ=8cos2θ 、AC2=4cos2θ+4sin2θ=4 、
AD2=4cos2θ+4sin2θ=4 、BC2=4cos2θ+4sin2θ=4 、
CD2=4cos2θ+4cos2θ=8cos2θ 、DA2=4cos2θ+4sin2θ=4
となり、四面体ABCDは、三角形の辺の長さが 2、2、2√2cosθ の等面四面体である。
このとき、 x2+y2=4 、y2+z2=4 、z2+x2=8cos2θ から、
x2=4cos2θ 、 y2=4(1−cos2θ)=4sin2θ 、z2=4cos2θ より、
x=2cosθ 、y=2sinθ 、z=2cosθ となり、これらを3辺とする直方体が存在する。