長方形の数　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　いま、６個の正方形が下図のように積まれている。

　　　　このとき、長方形（正方形も長方形の一つに数える。）は、何個あるだ
　　　ろうか？

　　　　地道に計算すれば、次のようであろう。


　　　　　　　　　　　　１×１長方形（正方形）は、６個
　　　　　　　　　　　　１×２長方形は、３個　　　２×１長方形は、３個
　　　　　　　　　　　　１×３長方形は、１個　　　３×１長方形は、１個
　　　　　　　　　　　　２×２長方形は、１個
　　　　　　　　　　　　　　　　　　　　　　　　　　　　以上から、長方形の総数は、１５個

　それでは、次のような場合、長方形は、何個あるだろうか？


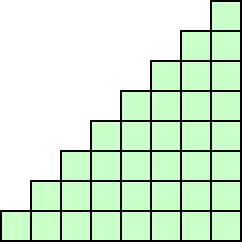
　　　　もちろん、この場合についても地道に計算する
　　　方法もあるが、煩雑だろうという気分が優先して、
　　　やってみようという気にはならない。多分、多くの
　　　人は、そう考えるだろう。

　　　　もう少し、求め方の工夫が必要なようだ。

　　　　横線から２本、縦線から２本とるといった通常
　　　の組合せの問題風に考えると、存在しえない長
　　　方形も数え上げてしまう。

　　　　そこで、そのような問題点を回避するような裏
　　　技が必要となる。


　図形外に補助線を１本引いて計算すると、「あっ！」という間にできてしまう。
とても「おそろしい」裏技である！

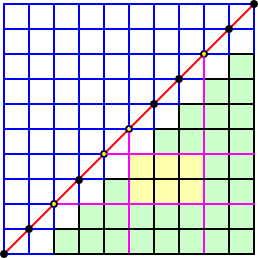　　　　左図において、１１個の点から、４個の点を
　　　選ぶ。

　　　　上段の２点においては、縦線、下段の２点
　　　においては、横線を引く。

　　　　このとき、２本の縦線と２本の横線により長
　　　方形が唯一つ定まる。

　　　　逆に、一つの長方形に対して、赤線上の４
　　　点が定まる。

　　　　従って、求める長方形の総数は、１１個の
　　　点から４個の点を選ぶ組合せの数に等しい。



　したがって、長方形の総数は、　₁₁C₄＝３３０　（個）である。

冒頭の場合、長方形の総数は、　₆C₄＝１５　（個）で求められる。

　一般に、

　　　ｎ 段の階段の場合、長方形の総数は、　　_ｎ+3Ｃ₄ （個）

であることが分かる。


（参考文献：根上生也・中本敦浩　著　　基礎数学力トレーニング　（日本評論社））


（追記）　平成３０年１１月２２日付け

　上記で考えたことをもう少し補足したい。

　下図のような格子状の図形がある。

　　　

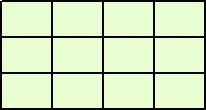
　この中に長方形がいくつあるかを問う問題は、順列・組合せの有名問題だろう。

もちろん、答えは、　₄Ｃ₂・₅Ｃ₂＝６０（個）　である。

　この問題に対して、下図のような階段状の図形があり、その中に長方形は全部で何個あ
るかと問われた場合、ちょっと考え込む人が多いのではないだろうか？

　　　

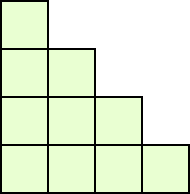
　頑張って目算してみると、３５個くらいありそうなのだが、ちょっと自信がない。

　この問題に対して、次のようなエレガントな解法が知られている。


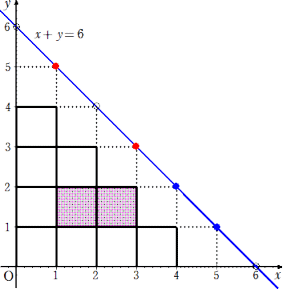　左図において、直線　ｘ＋ｙ＝６　を考える。

　長方形を構成する４辺との交点を４個選べば

よいので、求める長方形の個数は、

　　₇Ｃ₄＝３５（個）　となる。


（コメント）　このアイデアは、ものの本によると、
　　　　　　だいぶ昔に川邊さんという方が見いだ
　　　　　　されたとのことである。