
丂乽悢妛嘦乿偱妛傇恾宍偲曽掱幃偺崁栚偺拞偵乽椞堟乿偺寁嶼偑偁傞丅偙傟偼丄偁傞堄枴偱
乽偍奊昤偒偺帪娫乿偱丄擄夝側悢幃偲偦偺寁嶼偑搟煼偺傛偆偵墴偟婑偣傞拞偱堦庬偺僆傾
僔僗揑懚嵼偵側偭偰偄傞丅
丂偦偆偼尵偭偰傒偨傕偺偺丄乽椞堟乿偼丄嶼悢埲棃乽悢偲幃暘栰乿乽恾宍暘栰乿偲暿屄偵妛傫
偱偒偨傕偺偑梈崌偡傞堦偮偺僞乕僯儞僌億僀儞僩揑堄枴崌偄傕暪偣帩偮丅
丂惓曽宍偲偐嶰妏宍丄墌丄丒丒丒丂側偳偑丄偙偙偱偼悢幃偲偟偰岅傜傟丄偙偺妛廗埲崀丄惗搆
払偺恾宍偵懳偡傞庢傝埖偄偑旘桇揑偵恑曕偡傞丅
丂扨偵乽偍奊昤偒偺帪娫乿偱廔傢偭偰偼偄偗側偄廳梫側懁柺偑偁傞偺偱偁傞丅傑偨丄椞堟
偺奣擮偼丄柦戣偺恀棟廤崌偺昞尰偵傕妶梡偝傟丄悢妛偺榑棟偵怺偔娭傢偭偰偔傞廳梫側
暘栰偲尵偊傞丅
丂偙偺戝帠側乽椞堟乿偺妛廗偱丄乽侾揰戙擖朄乿偲偄偆曽朄偑偁傞偑丄偙偺曽朄偼丄嫵壢彂
偱怗傟傜傟傞偙偲偼側偄丅偟偐偟丄偍偦傜偔懡偔偺庴尡峑偱偼丄摉慠巜摫偝傟偰偄傞偼偢偺
曽朄偩傠偆丅
丂乽侾揰戙擖朄乿偱専嶕僜僼僩偵栤偄偐偗偰傒偰傕丄僸僢僩審悢偼丄侽 偱偁傞丅曽朄偼丄傛偔抦
傜傟偰偄傞偑丄偁傑傝擣抦偝傟偰偄側偄巹偩偗偺柦柤偐傕偟傟側偄丏丏丏丅
侾揰戙擖朄
丂暯柺偵偍偄偰丄暵偠傜傟偨嬋慄乮曻暔慄丄憃嬋慄傕娷傓乯 俥乮 倶 丆 倷 乯亖侽 偑梌偊傜
傟偰偄傞偲偡傞丅
丂偁傞侾揰 乮 倶0 丆 倷0 乯 偱丄 俥乮 倶0丆 倷0 乯亙侽丂傪枮偨偡偲偒丄
丂丂丂乮 倶0丆 倷0 乯 偲楢懕偱丄偐偮丄 俥乮 倶 丆 倷 乯亖侽 偲岎傢傜側偄嬋慄偱寢偽傟傞揰
乮 倶 丆 倷 乯 偼丄丂俥乮 倶 丆 倷 乯亙侽丂傪枮偨偡丅
乮棯徹乯丂傕偟丄丂俥乮 倶 丆 倷 乯亜侽丂偲壖掕偡傞偲丄俥乮 倶 丆 倷 乯偑楢懕偱偁傞偙偲偵傛傝丄
丂丂丂丂丂俥乮 倶1 丆 倷1 乯亖侽丂偲側傞揰 乮 倶1 丆 倷1 乯 偑懚嵼偡傞丅偡側傢偪丄揰 乮 倶1 丆 倷1 乯 偑
丂丂丂丂嬋慄忋偺揰偱偁傞偙偲偐傜丄壖掕偵柕弬偡傞丅傛偭偰丄丂俥乮 倶 丆 倷 乯亙侽丂丂乮徹廔乯
椺丂晄摍幃丂倷 亜 倶亄侾丂偑昞偡椞堟偼丄捈慄丂倷 亖 倶亄侾丂偺忋懁偱偁傞丅
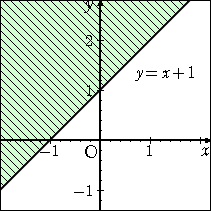
丂丂丂丂偙偺栤戣偵丄侾揰戙擖朄傪揔梡偟偰傒傛偆丅
丂丂丂丂丂丂俥乮 倶 丆 倷 乯 亖 倷亅倶亅侾丂偲偍偔丅
丂丂丂丂俥乮 倶 丆 倷 乯亜侽丂偲側傞揰傪尒偮偗傟偽傛偄丅
丂丂丂丂丂帋偟偵丄丂俥乮 侽 丆 俀 乯 亖 俀亅侽亅侾 亖 侾 亜侽
丂丂丂丂傛偭偰丄揰乮 侽 丆 俀 乯傪娷傓椞堟偑媮傔傞椞堟偱偁
丂丂丂傞丅乮嵍恾乯
椺丂晄摍幃丂倶 亙 侾丂偑昞偡椞堟偼丄捈慄丂倶 亖 侾丂偺嵍懁偱偁傞丅
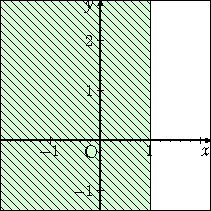
丂丂丂丂偙偺栤戣偵丄侾揰戙擖朄傪揔梡偟偰傒傛偆丅
丂丂丂丂丂丂俥乮 倶 丆 倷 乯 亖 倶亅侾丂偲偍偔丅
丂丂丂丂俥乮 倶 丆 倷 乯亙侽丂偲側傞揰傪尒偮偗傟偽傛偄丅
丂丂丂丂丂帋偟偵丄丂俥乮 侽 丆 俀 乯 亖 侽亅侾 亖 亅侾 亙侽
丂丂丂丂傛偭偰丄揰乮 侽 丆 俀 乯傪娷傓椞堟偑媮傔傞椞堟偱偁
丂丂丂傞丅乮嵍恾乯
椺丂晄摍幃丂倶2亄倷2 亜 侾丂偑昞偡椞堟偼丄墌丂倶2亄倷2 亖 侾丂偺奜晹偱偁傞丅
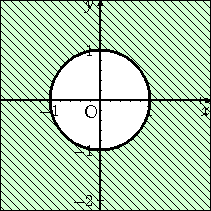
丂丂丂丂偙偺栤戣偵丄侾揰戙擖朄傪揔梡偟偰傒傛偆丅
丂丂丂丂丂丂俥乮 倶 丆 倷 乯 亖 倶2亄倷2亅侾丂偲偍偔丅
丂丂丂丂俥乮 倶 丆 倷 乯亜侽丂偲側傞揰傪尒偮偗傟偽傛偄丅
丂丂丂丂丂帋偟偵丄丂俥乮 侽 丆 俀 乯 亖 侽亄係亅侾 亖 俁 亜侽
丂丂丂丂傛偭偰丄揰乮 侽 丆 俀 乯傪娷傓椞堟偑媮傔傞椞堟偱偁
丂丂丂傞丅乮嵍恾乯
丂偙偺傛偆偵丄
丂丂丂丂丂丂丂丂丂嫬奅慄丂倷 亖 俥乮倶乯丂偺丂忋懁丂丄丂壓懁
丂丂丂丂丂丂丂丂丂嫬奅慄丂倶 亖 倎丂偺丂塃懁丂丄丂嵍懁
丂丂丂丂丂丂丂丂丂嫬奅慄丂倶2亄倷2 亖 倰2丂偺丂撪晹丂丄丂奜晹
偲偄偆椞堟偺寁嶼偑丄扨側傞懡崁幃偺晞崋偺寁嶼偵摑堦偝傟傞丅
丂傑偨丄侾揰戙擖朄傪梡偄傞偲丄暯柺忋偺揰偺埵抲娭學偺攃埇偵傕桳岠偱偁傞丅
椺丂暯柺忋偵偍偄偰丄捈慄 倶亄俀倷亅係亖侽丂偵娭偟偰丄俀揰 俙乮 亅俀 丆 俀 乯丄俛乮 俁 丆 亅俀 乯
丂丂偼摨偠懁偵偁傞揰偱偁傞偙偲傪帵偣丅
乮夝乯丂俥乮 倶 丆 倷 乯 亖 倶亄俀倷亅係丂偲偍偔偲丄
丂丂丂丂丂丂丂俥乮 亅俀 丆 俀 乯 亖 亅俀亄係亅係 亖 亅俀 亙 侽
丂丂丂丂丂丂丂俥乮 俁 丆 亅俀 乯 亖 俁亅係亅係 亖 亅俆 亙 侽
丂丂丂側偺偱丄
丂丂丂丂俀揰俙乮 亅俀 丆 俀 乯丄俛乮 俁 丆 亅俀 乯偼丄捈慄偵娭偟偰摨偠懁偵偁傞揰偱偁傞丅丂乮廔乯
丂恾帵偡傞偲丄壓恾偺傛偆偱偁傞丅
丂丂丂丂丂丂丂

丂偙偺峫偊曽偼丄師偺傛偆側栤戣偵墳梡偝傟傞丅
椺丂捈慄 倶亄俀倷亅係亖侽丂忋傪摦偔揰 俹 偑偁傞丅暯柺忋偵偍偄偰丄俀揰 俙乮 亅俀 丆 俀 乯丄
丂丂俛乮 俁 丆 亅俀 乯 偲偡傞丅偙偺偲偒丄丂俙俹亄俛俹 偑嵟彫偲側傞揰 俹 偺嵗昗傪媮傔傛丅
乮夝乯丂俀揰俙乮 亅俀 丆 俀 乯丄俛乮 俁 丆 亅俀 乯偼丄捈慄偵娭偟偰摨偠懁偵偁傞揰偵偁傞偺偱丄
丂丂丂捈慄偵娭偡傞揰 俛 偺懳徧揰 俠 傪媮傔傞偲丄捈慄 俙俠 偲捈慄 倶亄俀倷亅係亖侽丂偺
丂丂丂岎揰 俢 偑媮傔傞揰偲側傞丅
丂丂丂丂捈慄 俛俠 偺曽掱幃偼丂倷亖俀倶亅俉丂側偺偱丄揰 俫 偺嵗昗偼丄乮 係 丆 侽 乯偲側傞丅
丂丂丂慄暘俛俠偺拞揰偑俫偲側傞偺偱丄揰 俠 偺嵗昗偼丄乮 俆 丆 俀 乯偲側傞丅
丂丂丂偟偨偑偭偰丄媮傔傞揰 俢 偺嵗昗偼丄乮 侽 丆 俀 乯偲側傞丅丂乮廔乯
丂侾揰戙擖朄偼丄椞堟偑暋嶨偱偁傟偽偁傞傎偳丄偦偺岠壥偼愨戝偱偁傞丅
丂丂丂丂俥乮 倶 丆 倷 乯亜侽丂偲側傞揰乮 倶 丆 倷 乯偺廤崌偼丄惓椞堟
丂丂丂丂俥乮 倶 丆 倷 乯亙侽丂偲側傞揰乮 倶 丆 倷 乯偺廤崌偼丄晧椞堟
偲尵傢傟傞丅
丂俥乮 倶 丆 倷 乯偑楢懕偱偁傞尷傝丄嫬奅慄傪墇偊傞偛偲偵惓椞堟偲晧椞堟偼岎屳偵弌尰偡傞丅
丂偟偨偑偭偰丄偳偙偐堦晹暘偺椞堟偺晞崋偑暘偐傟偽丄屻偼堭偯傞幃偵偡傋偰偺椞堟偺晞
崋偑暘偐傞丅
椺丂師偺椞堟傪丄晄摍幃傪梡偄偰昞偣丅
丂丂丂丂
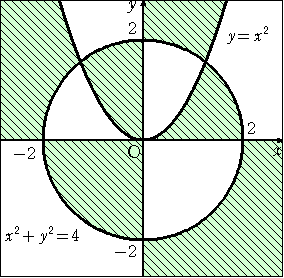
丂偙偺栤戣傪嫵壢彂揑側夝摎偱峫偊傞偲丄偍偦傜偔懡偔偺曽偼廂廍偑偮偐側偄夝摎偵壵棫
偪傪妎偊傞偵堘偄側偄丅
丂偙偆偄偆僞僀僾偺栤戣偙偦丄侾揰戙擖朄偺撈抎応偩傠偆丅
乮夝乯丂嫬奅慄偼丄師偺係庬椶偱偁傞丅
丂丂丂丂倶亖侽丂丄丂倷亖侽丂丄丂倶2亄倷2亖係丂丄丂倷亖倶2
丂丂丂偦偙偱丄懡崁幃丂俥乮 倶 丆 倷 乯 亖 倶倷乮倶2亄倷2亅係乯乮倷亅倶2乯丂偵偍偄偰丄
丂丂椞堟撪偺揰乮 亅侾 丆 亅侾 乯偵偍偗傞晞崋傪挷傋傞丅
丂丂丂丂俥乮 亅侾 丆 亅侾 乯 亖 乮亅侾乯乮亅侾乯乮侾亄侾亅係乯乮亅侾亅侾乯 亖 係 亜 侽
丂丂側偺偱丄媮傔傞晄摍幃偼丄丂倶倷乮倶2亄倷2亅係乯乮倷亅倶2乯亜侽丂偲側傞丅丂乮廔乯
丂丂丂埲壓丄岺帠拞