
統計学において、平均と分散の計算は、必須の、避けて通れない大切なポイントである。
いろいろな分布を用いた推定・検定において、本質的な役割を果たす。
確率変数をXとすると、Xの平均E(X)・分散V(X)は、次のように定義される。
離散的な確率変数Xに対して

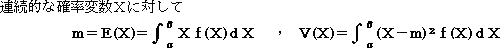
但し、Pk=P(X=XK)は確率で、確率密度関数をf(X)とする。
(もっと詳しい説明が欲しい場合は、こちらを参照)
分散を求める公式として、次の公式はよく知られている。
《重要公式》 V(X)=E(X2)−E(X)2
いろいろな分布について、平均と分散の公式が知られている。
(1) Xが2項分布B(n,p)に従うとき、
E(X)=np 、 V(X)=npq (ただし、q=1−p)
(2) Xが正規分布N(m,σ2)に従うとき、
E(X)=m 、 V(X)=σ2
(3) Xがポアソン分布P(λ)に従うとき、
E(X)=λ 、 V(X)=λ
ポアソン分布は、起こる確率が十分小さい事象を多数回独立に試行したときに生ずる
分布である。
これらの公式を証明しようとするとき、かなり複雑で特殊な計算が我々を待ち受ける。この
計算を統一的かつ簡単に求める公式があるので紹介したい。
確率変数Xの積率母関数(Moment Generating Function) g(θ)を、次の式により定義する。
g(θ)=E(exp(θX))
定理 E[Xk]=g(k)(0) が成り立つ。
従って、E(X)=g’(0) 、V(X)=g”(0)−g’(0)2 が成り立つ。
定理 各分布の積率母関数は、次の式で与えられる。
(1) Xが2項分布B(n,p)に従うとき、g(θ)=(pexpθ+q)n (ただし、q=1−p)
(2) Xが正規分布N(m,σ2)に従うとき、g(θ)=exp(mθ+(σθ)2/2)
(3) Xがポアソン分布P(λ)に従うとき、g(θ)=exp(−λ(1−expθ))
この定理を用いれば、平均・分散の計算は、単にθ=0におけるg(θ)、g’(θ)の微分係数の
計算に帰着される。実際の計算は、読者の演習として残しておこう。
(この裏技の優秀性は、実際に計算した場合にのみ理解されることでしょう!.....塾長)
(参考文献:M.Loeve 著 Probability theory
W.Feller 著 An introduction to Probability theory vol.2)