予備校の現役講師（とても有名な方らしい！）の方から、数学の指導法を伺う機会があっ
た。
（板書の際、チョークでの点線の描き方が見事であった。お話もさることながら、点線の描き方に目を奪われた。
こう書いてしまうと、講師の方のお名前が分かってしまうかな？後で、一緒にお話を聞いたＮさんに、点線の描き
方を教わって、描けるようになった。とても感動した！Ｎさんに感謝！）
今の子は、人の前で失敗することを極端に嫌がるので、計算の失敗例をこちらから示して
あげるとか、できるだけ途中計算を省かずに計算の流れを示してあげるとか、直感的なこと
も言葉で表してあげるといいとか、いろいろ私自身反省させられるお話であった。
また、問題文の意味するところの図が書けない理由として、「それは、問題文を読んでいな
いから！一緒に読んであげるといい！」と断言されたのには、思わず唸ってしまった。なぜか、
目から鱗が落ちたような爽快さを感じた。
私自身、予備校で講義を受けた経験は全くないが、数学を分からせてあげようという心意
気に溢れた方に接し、予備校に対する印象が変わってしまった。
それまでは、予備校は受験テクニックを教えるところで、味気ないところと考えていたが、
実際は異なっていた。受験テクニックを覚えても覚えきれない中で、最後に頼れるのは、や
はり教科書的なことがしっかりできているかだという。予備校では、そこのところをしっかり
指導しているという。
世の受験校といわれるところでは、問題練習を通して、受験テクニックに走る授業になり
がちである。数学の指導法として、予備校と学校の根本的な考え方の相違に、ただ驚くば
かりである。
たとえば、微分積分の面積計算で、(−１/６)(β−α)3 という公式は、必ず教えていると思
う。センター試験では有用な公式で、これを知っているかいないかで、時間的に大きなハン
デとなる。ところが、記述式の問題で、この公式を証明なしで使うと減点するという大学が
あるという。部分積分を使えば簡単に示せるのに、それをしていないからということで減点
らしい。
上記の公式同様、よく大学入試懇談会などで話題になるのが、ロピタルの定理を証明な
しで使ってよいかという問題である。
以前は知っているものは何でも使ってよいという風潮であったが、最近はどうも風向きが
違うようだ。別な形で簡単に示せるものに、わざわざロピタルの定理を使うのはまかりなら
んということらしい。
たとえば、皆さんは、次の極限値を求めるとき、どう教えるだろうか？
ロピタルの定理を用いて、
と教えてはいないだろうか？
このロピタルの定理を用いた解法も、大学入試の採点者の評判は芳しくないらしい。
この場合、次のように教えるといいそうだ。
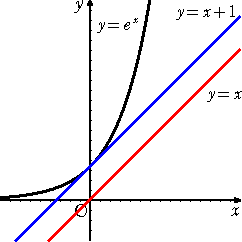左図からも分かるように、指数関数 ｙ＝ｅｘ の点（０，１）における接線の方程式 ｙ＝ｘ＋１ に
ついて、
ｅｘ ≧ ｘ＋１ すなわち、 ｅｘ ＞ ｘ
である。
したがって、
ｅｔ/２ ＞ ｔ/２ より、（ｅｔ/２）2 ＞（ ｔ/２）2
すなわち、 ｅｔ ＞ ｔ2/４ となる。
このとき、 ０＜ｔ/ｅｔ＜４/ｔ で、ｔ → ∞ のとき、
ｔ/ｅｔ → ０ が成り立つ。
とかくテクニックに走りがちな受験勉強だが、教科書で学んだことで十分対応できるとい
うことを再認識させられた。策に溺れず、堅実が一番ということだろう！