グラフを描くコツ　　　　　　　　　　　　　　　　　　　　　　　　　　　

　これから述べることは果たして裏技と呼べるものかどうか、実は自信がない。

たとえば、今まで習っていないような関数のグラフ
　　　　　　　
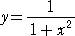
を描かなければならないとき、あなたはどう考えるだろうか？

　いろいろな情報を集めて、グラフの予想をたてるに違いない。
たとえば、ｘ＞０　では、ｘ²　と　ｘ　は同じように単調増加であるから、
　　　　　　　
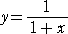
と似たグラフになると判断される。
　ただし、０ ＜ ｘ ＜ １ では、ｘ²　＜　ｘ　であり、ｘ ＞ １ では、ｘ²　＞　ｘ　であることに注意
すれば、０ ＜ ｘ ＜ １ と　ｘ ＞ １ の部分で多少凹凸に変化があることも分かる。

以上を参考にすれば、グラフを描くことは易しい。（下図）

　　　

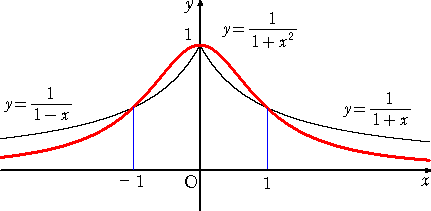
　このように未知のグラフを描こうとする場合、既知のグラフとの関連性を考えると、その形
がおぼろげながら見えてくる。

　また、関数によっては、特別な意味を持つ変数 ｘ の値がある。

分数関数

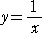は、ｘ＝０ が特別な点である。これは、漸近線となる。

また、２次関数 ｙ＝ａｘ² においては、ｘ＝０ である。この値は、軸の方程式ともとれるし、頂
点の ｘ 座標ともとれる。２次関数においては、この点をおさえることが肝要である。

　すなわち、この点の近くで関数の値がどう変化するかを見れば、グラフは描けたも同然で
ある。

　したがって、たとえば、２次関数 ｙ＝ａ（ｘ−３）²＋４ においては、ｘ＝３ の近くで値を調べ
ればいいことになる。

　また、２次関数 ｙ＝ｘ²＋４ｘ−５ の場合は、ｙ＝０ となる点の近くで調べればよい。

　このような着眼点は、数学が得意な人にとっては教えられなくても自然に身に付く嗅覚だ
と思うが、数学が不得意な人にとっては、気がつきにくく、忘れやすい所でもある。

　関数は、式だけを見ては到底十分な理解は望めない。グラフを描いて、関数を視覚化す
ることによってのみ関数の理解が進み、本質が見えてくる。

　昨今、パソコンで簡単にグラフが描けるようになったが、初心者のうちはパソコンに頼ら
ず、自力で計算して描くことをお勧めする。その方が関数の振る舞いが痛いほどよく分か
るから！

（参考文献：　Ｉ．Ｍ．ゲルファント、Ａ．シェン　著、富永星、赤尾和男訳
　　　　　　　　　　　　　　ゲルファント先生の学校に行かずにわかる数学　１　（岩波書店））