
正弦定理・余弦定理は、図形の計量問題ではなくてはならない最大の武器である。その
証明は、いろいろ考えられる。( → 参考 : 正弦定理と余弦定理)
ここでは、等積変形による証明を紹介したいと思う。以下では、鋭角三角形で考えている
が、一般の場合にも同様に示される。
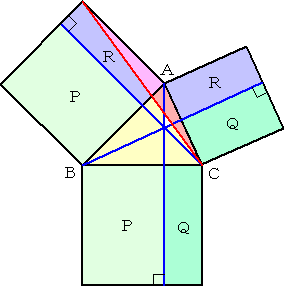
左図のように、△ABC において、各辺
を一辺とする正方形を描き、三角形の各
頂点より垂線を下ろし、各正方形を分割
する。
このとき、等積変形により、図中の面積
P、Q、R は、それぞれ等しい。
この幾何学的性質を用いると、余弦定
理の証明は、三角形の面積の公式の証
明に帰される。
(証明) BC2=P+Q
=(P+R)+(Q+R)−2R
=AB2+AC2−2×2×(上図の赤い部分の三角形の面積)
=AB2+AC2−2×2×((1/2)×AB×AC×sin(90°+A))
=AB2+AC2−2・AB・AC・cosA
(証終)
教科書的には、余弦定理を学んだ後、三角形の面積に進むので、上記の方法は、最初
の導入には使えないかもしれない。(教科書によっては、三角形の面積を余弦定理の前に
おいているところもある。) 三角比を全て学んだ後、振り返りのためにこのような話題を提
供すれば、定着率は多少向上し、学習者の興味・関心が増すかもしれない。
(コメント: 三平方の定理に似た証明で、その鮮やかさに魅入られます。)
(追記) 平成22年11月18日付け
当HPの読者の T.I.さんから、上記の証明をさらに分かり易くする方法をご教示いただ
いた。
上図で、証明中、Rを三角形の面積から導いていますが、
R=c×(b×cosA)=b×(c×cosA)
であることは、直ちにわかることなので、これを使えば、三角形の面積公式にとらわれなく
てもいけそうですね。
(コメント) T.I.さん、ありがとうございます。
sin(90°+A)=cosA が気になる部分で、T.I.さんの方が初等的ですね!