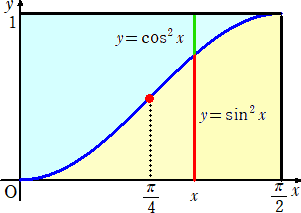
丂悢妛嘥偺嶰妏斾偱丄惓尫乮倱倝値乯傗梋尫乮們倧倱乯傪妛傇丅悢妛嘥偱偼恾宍偺寁検乮惓尫掕棟丒
梋尫掕棟乯偑庡側僥乕儅偩丅
丂悢妛嘦偱弶傔偰娭悢偲偟偰偺惓尫丒梋尫傪妛傃丄偦偺廃婜揑側僌儔僼偺旤偟偝偵怱傪懪偨
傟傞丅庼嬈偱偼椉幰偺僌儔僼傪暿乆偵彂偔偑丄壓恾偐傜傕暘偐傞傛偆偵丄偦傟傜偼摨宍偱偁
傞丅
丂丂丂丂丂丂丂
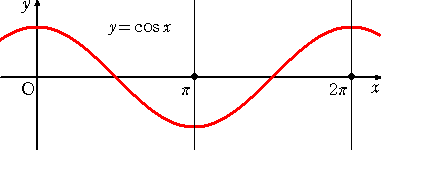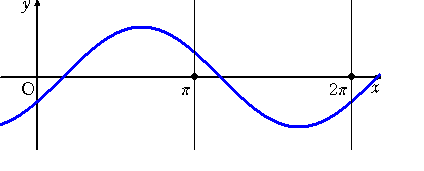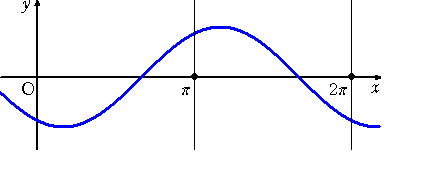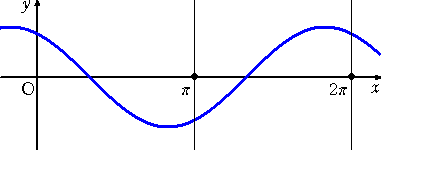
丂忋恾偱偼丄倷亖們倧倱倶丂偺僌儔僼傪婲揰偲偟偰丄丂倷亖們倧倱乮倶亅兤乯丂乮兤偼幚悢乯偺僌儔僼傪彂偐
偣偨傕偺偱偁傞丅
丂們倧倱乮倶亅兾/俀乯亖倱倝値倶丂側偺偱丄搑拞偱丄丂倷亖倱倝値倶丂偺僌儔僼偑弌尰偡傞丅
丂惓尫乮倱倝値乯傗梋尫乮們倧倱乯偼掕媊偙偦堦尒堘偆傛偆偵巚偊傞偑丄椉幰偼屳偄偵枾愙偵娭學偟
偰偍傝丄奣擮揑偵偼摨庬偺傕偺偱偁傞丅
丂惓尫乮倱倝値乯傗梋尫乮們倧倱乯偵偮偄偰惗搆傪擸傑偣傞偺偼丄偦偺岞幃偺朙晉偝偱偁傞丅偙傟偵
偮偄偰丄暫屔導棫晲屔憫憤崌崅峑偺擁揷婱帄愭惗偑乽倱倝値僋儘僗乿偲偄偆柺敀偄妎偊曽傪峫
埬偝傟偰偄傞丅乮仺丂嶲峫丗悢尋捠怣丗乽暯峴堏摦傪夞揮偱乿丂丄乽亀倱倝値僋儘僗亁偱旝暘偡傞乿乯
丂丂丂倱倝値乮倶亄兾/俀乯亖們倧倱倶丂丄丂們倧倱乮倶亄兾/俀乯亖亅倱倝値倶丂丂偑惉傝棫偪丄偝傜偵丄
丂丂倱倝値乮倶亄兾/俀乯亖們倧倱倶丂傛傝丄丂亅倱倝値乮倶亄兾/俀乯亖亅們倧倱倶
丂丂們倧倱乮倶亄兾/俀乯亖亅倱倝値倶丂傛傝丄丂亅們倧倱乮倶亄兾/俀乯亖倱倝値倶
丂偑惉傝棫偮丅
丂偙偺偙偲偐傜丄丂乽亄兾/俀乿偲偄偆憖嶌偵傛傝丄
丂倱倝値倶丂仺丂們倧倱倶 丄們倧倱倶丂仺丂亅倱倝値倶 丄亅倱倝値倶丂仺丂亅們倧倱倶 丄亅們倧倱倶丂仺丂倱倝値倶
偲弴師曄壔偡傞偙偲偑尒偰庢傟傞丅
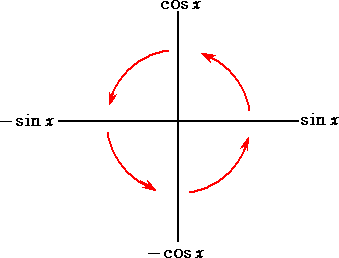
丂偙傟傜偺娭學幃偱丄乽亄兾/俀乿偺暯峴堏摦傪丄壓恾偺傛偆偵丄乽兾/俀 偺夞揮乿偲峫偊傞偙偲
偑丄乽倱倝値僋儘僗乿偲偄偆傕偺偺峫偊曽偺傛偆偩丅
丂丂丂丂丂丂丂丂丂
丂偙偺曽朄傪梡偄傞偲丄岞幃傕帺慠偲摢偵晜偐傃忋偑偭偰偔傞傛偆側婥偑偡傞丅
丂傑偨丄
丂倱倝値倶丂仺丂們倧倱倶 丄們倧倱倶丂仺丂亅倱倝値倶 丄亅倱倝値倶丂仺丂亅們倧倱倶 丄亅們倧倱倶丂仺丂倱倝値倶
偲偄偆娭學偼丄惓偵旝暘偺岞幃偱偁傞丅
丂偟偨偑偭偰丄忋恾偼丄嶰妏娭悢偺曃妏岞幃偺妎偊曽偺傒側傜偢丄旝暘傗愊暘偺岞幃偺妎
偊曽偵傕巊偊傞偲偄偆傢偗偩両
丂偙偺傛偆側怴偟偄尒曽丒峫偊曽傪敪尒偝傟偨暫屔導棫晲屔憫憤崌崅峑偺擁揷婱帄愭惗偵
宧堄傪昞偟偨偄丅
乮捛婰乯丂椷榓俀擭俇寧俈擔晅偗