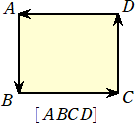
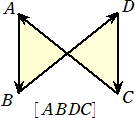
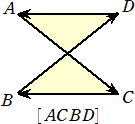
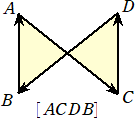
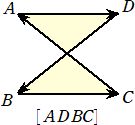
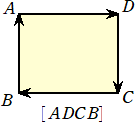
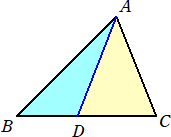有向三角形 
△ABCを作図する場合、一筆書きのように描く人が多いと思う。(私の場合は、∠のように
描いた後、|で締めくくるが...)
一筆書きの場合、2つの書き方がある。
前者の場合、△ABC と向きを込めて書くことにしよう。すると、後者の場合は、△ACBと
なる。このように、頂点の並ぶ順序を意識することにより、向きも意識される。
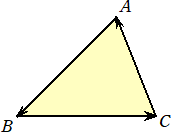
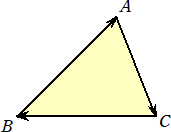
頂点を順々に繋ぐ辺からなる閉じた図形に沿って運動する点の軌跡として三角形を捉え
る考え方が、有向三角形である。
有向三角形の面積は次のように定義される。
3点A、B、Cを頂点とする三角形の面積をSとおくと、
頂点の並びの順序が反時計回りのとき、 △ABC=S
頂点の並びの順序が時計回りのとき、 △ACB=−S
有向三角形の面積の公式
座標平面上の3点A(a1,a2)、B(b1,b2)、C(c1,c2)において、有向三角形ABCの面
積は、
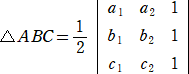
で与えられる。
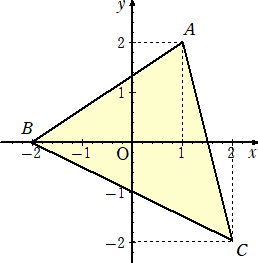
問題 座標平面上の3点A(1,2)、B(−2,0)、C(2,−2)において、△ABCおよび
△ACBの面積をそれぞれ求めよ。
(解) 面積の公式により、
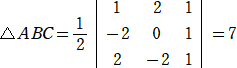
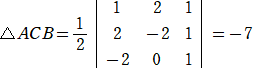 (終)
(終)
(コメント) 確かに、頂点の並びの順序が反時計回りのときは、(面積)>0、頂点の並びの
順序が時計回りのときは、(面積)<0 ということが実感できますね!
この面積に向きを持たせるという考え方は、初等幾何において効果的な働きを示す。
例えば、
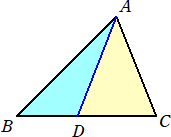
においては、三角形ABCの面積が辺BCの内分点Dにより、
三角形ABC=三角形DAB+三角形DCA
と和の形に分割される。
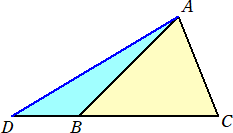
においては、三角形ABCの面積が辺BCの外分点Dにより、
三角形ABC=三角形DCA−三角形DAB
と差の形に分割される。
このようにBCの分点の種類によって、式の表現が異なるわけであるが、有向三角形の
面積の概念を用いれば、実は、1本の式でまとめることが出来る。すなわち、
直線BC上の任意の点Dに対して、 △ABC=△DAB+△DCA
DがBCの内分点の場合、三角形DABと三角形DCAは同じ向きで、面積の和になる。
DがBCの外分点の場合、三角形DABと三角形DCAは異なる向きで、面積の差になる。
この場合、面積の符号の定義から、「三角形DCA−三角形DAB」を意味する。
同様にして、
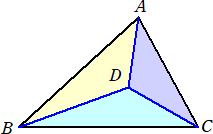
平面上の任意の点Dに対して、 △ABC=△DAB+△DBC+△DCA
が成り立つ。これも三角形の向きを考えれば、面積の正負が定まるので、納得できる公式
だろう。
上図の(イ)において、△DAB、△DBC、△DCAはすべて反時計周りの向きで、面積は正
である。
上図の(ロ)において、△DAB、△DCAはともに反時計周りの向きで、面積は正であるが、
△DBCは時計回りで、面積は負である。
上図の(ハ)において、△DAB、△DCAはともに時計周りの向きで、面積は負であるが、
△DBCは反時計回りで、面積は正である。
確かに、三角形ABCの面積が、Dの位置によらず
△ABC=△DAB+△DBC+△DCA
によって得られることに驚かされる。これが有向三角形の底力だろう。
有向三角形を一般化して、有向多角形も考えることができる。
有向四角形に限定しても、いろいろな場合が考えられる。
平面上の4点A、B、C、Dに対して、
がある。一般には、次のような有向多角形も考えられる。
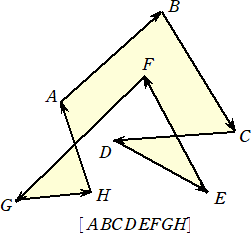
このような有向多角形に対して、面積はどのように考えればよいのだろうか?
これに対して、有向多角形[ABC・・・GH]の面積は、次の式で計算される。
平面上の任意の点Oに対して、
[ABC・・・GH]=[OAB]+[OBC]+・・・+[OGH]+[OHA]
この式は、有向三角形における面積の公式
△ABC=△DAB+△DBC+△DCA
の一般化になっている。
例 平面上の4点A(1,1)、B(−1,1)、C(−1,−1)、D(1,−1)に対して、有向四角
形[ABCD]、[ABDC]、[ADCB]の面積をそれぞれ求めよ。
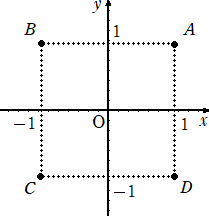
(解) [ABCD]=[OAB]+[OBC]+[OCD]+[ODA]=1+1+1+1=4
[ABDC]=[OAB]+[OBD]+[ODC]+[OCA]=1+0−1+0=0
[ADCB]=[OAD]+[ODC]+[OCB]+[OBA]=−1−1−1−1=−4 (終)
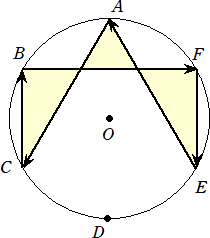
問題 半径2の円周上に等分点A、B、C、D、E、Fをとる。このとき、次の有向六角形の
面積を求めよ。
|
(1) |
|
(2) |
| |
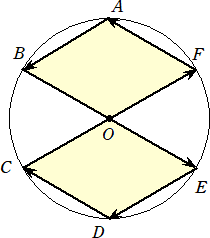 |
|
 |
(解)(1) [ABEDCF]=[OAB]+[OBE]+[OED]+[ODC]+[OCF]+[OFA]
= +0−
+0− −
− +0+
+0+ =0
=0
(2) [ABCDFE]=[OAB]+[OBC]+[OCD]+[ODF]+[OFE]+[OEA]
= +
+ +
+ +
+ −
− +
+ =4
=4 (終)
(終)
(追記) 令和4年10月21日付け

において、[ABEDCF]を計算するとき、
[OAB]+[OBE]+[OED]+[ODC]+[OCF]+[OFA]
で求められたが、よく見ると、この計算は、
[OBO]=[OOF]=[OOE]=[OCO]=0 なので、
([OAB]+[OBO]+[OOF]+[OFA])+([OOE]+[OED]+[ODC]+[OCO])
すなわち、 [ABEDCF]=[OFAB]+[OEDC] と分解できることが分かる。
この場合、Oは、辺BEと辺CFの交点で、辺同士のただ1回の交叉となっていることが肝
要である。
[OFAB]は反時計回りで、面積は正なのに対して、[OEDC]は時計回りで、面積は負と
なる。
よって、[OFAB]と[OEDC]は図形として同形なので、 [ABEDCF]=0 であることは
自明となる。
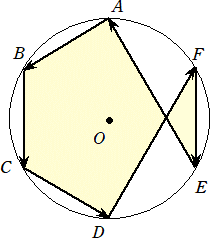
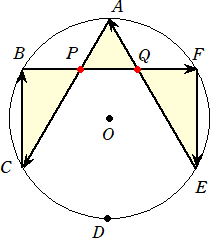
この性質を利用すると、
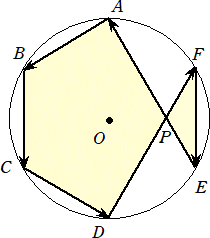
における[ABCDFE]の計算は、
[ABCDFE]=[ABCDP]+[PFE]
と分解され、[ABCDP]は反時計回りで面積は正、[PFE]は時計回りで面積は負となる。
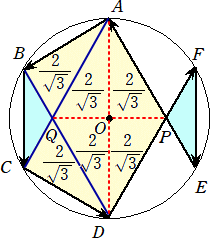
上図において、△QBCと△PFEは同形で面積は同じなので、
[ABCDFE]=(2/ )×6=4
)×6=4
となり、先の計算結果と一致する。
問題 半径2の円周上に等分点A、B、C、D、E、Fをとる。このとき、次の有向五角形の
面積を求めよ。
(解) [ACBFE]=[OAC]+[OCB]+[OBF]+[OFE]+[OEA]
= −
− −
− −
− +
+ =−
=− (終)
(終)
面積の定義から、点Oは平面上の任意の点なので何でもいいわけであるが、下図で、点
Pをもとに計算してみよう。
[ACBFE]=[PAC]+[PCB]+[PBF]+[PFE]+[PEA]
=0−(2/3) +0−(4/3)
+0−(4/3) +
+ =−
=−
(コメント) 点PやQで計算すれば楽ができるかなと思いましたが、意外と大変でしたね!
有向でない三角形PBCの面積S=(2/3)
有向でない三角形APQの面積T=(1/3)
から、 [ACBFE]=T−2S という関係が成り立つんですね...。
実際に、
[ACBFE]=[PAC]+[PCB]+[PBF]+[PFE]+[PEA]
=[PCB]+[PFE]+[PEA]
ここで、 [PFE]=[PQE]+[QFE] 、[PEA]=[PEQ]+[PQA] なので、
[ACBFE]=[PCB]+[PQE]+[QFE]+[PEQ]+[PQA] において、
[PCB]=[QFE] 、[PQE]+[PEQ]=0 なので、
[ACBFE]=[PQA]+2*[PCB]
ここで、[PQA]の面積は正、[PCB]の面積は負から、 [ACBFE]=T−2S となる。
以上の計算を参考にすれば、一般的に、
有向多角形において、ある2つの辺が互いに1度だけ交差するとき、有向多角形の
面積は、多角形が分割されている2つの有向でない多角形の面積の差に等しい
と言えることが分かる。
例えば、

の有向多角形の面積が0であることも即座に納得できることだろう。
問題 半径2の円周上に等分点A、B、C、D、Eをとる。このとき、次の有向五角形の面積
を求めよ。
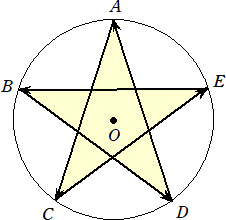
(解) [ACEBD]=[OAC]+[OCE]+[OEB]+[OBD]+[ODA]=5*[OAC]
ここで、 [OAC]=(1/2)・2・2・sin144°=2sin36°
36°=θとおくと、 5θ=180° なので、 sin3θ=sin(180°−2θ)=sin2θ
3sinθ−4sin3θ=2sinθcosθ より、 3−4sin2θ=2cosθ
sin2θ=1−cos2θ を代入して整理すると、 4cos2θ−2cosθ−1=0
よって、 cosθ=(1+ )/4 なので、 sinθ=
)/4 なので、 sinθ=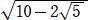 /4
/4
以上から、 [ACEBD]=(5/2)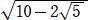 となる。 (終)
となる。 (終)
(コメント) [ACEBD]の値は、実際の星形の面積よりも中の五角形の分が多い。
問題 半径2の円Oの直径をABとし、弧AB上に2点P、Qを、∠AOP=α、∠POB=β
となるようにとる。ただし、α、β>0で、α+β<πとする。

このとき、有向四角形[ABPQ]の面積の値は、0とは異なることを示せ。
(解) [ABPQ]=[OAB]+[OBP]+[OPQ]+[OQA] において、
[OAB]=0 、[OBP]=2sinα 、[OPQ]=−2sinβ 、[OQA]=2sin(α+β)
なので、
[ABPQ]=2(sinα−sinβ+sin(α+β))
=4(cos((α+β)/2)sin((α−β)/2)+sin((α+β)/2)cos((α+β)/2))
=4cos((α+β)/2)(sin((α−β)/2)+sin((α+β)/2))
=8cos((α+β)/2)sin(α/2)cos(β/2)
今、[ABPQ]=0 と仮定すると、
cos((α+β)/2)=0 、sin(α/2)=0 、cos(β/2)=0
の何れかが成り立つ。
cos((α+β)/2)=0 のとき、 (α+β)/2=π/2 から、 α+β=π
しかるに、これは、 0<α+β<π に矛盾する。
sin(α/2)=0 のとき、 α/2=0 から、 α=0
しかるに、これは、 α>0 に矛盾する。
cos(β/2)=0 のとき、 β/2=π/2 から、 β=π
しかるに、これは、 β<π に矛盾する。
以上から、背理法により、 [ABPQ]≠0 であることが示された。 (終)
(コメント) 上図において、線分AQとBPの交点をRとするとき、[ABPQ]≠0 という事実
から、
有向でない三角形ABRの面積≠有向でない三角形PQRの面積
であることが示された。
有向多角形の性質を用いなくとも、直接に上記の事実を示すことは可能だと思われるが、
若干大変な計算を強いられることだろう。両者の解法を比較すれば、有向多角形の概念の
有用性が分かると思う。
この問題をさらに掘り下げて、次の問題はどうだろうか?
問題 半径2の円Oの直径をABとし、弧AB上に2点P、Qを、∠AOP=α、∠POB=β
となるようにとる。ただし、α、β>0で、α+β<πとする。また、弧PQの中点をS
とおく。
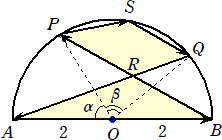
このとき、有向でない三角形RABの面積の値と有向でない四角形PSQRの面積の値が
等しくなる場合があることを示せ。
(解) [ABPSQ]=[OAB]+[OBP]+[OPS]+[OSQ]+[OQA] において、
[OAB]=0 、[OBP]=2sinα 、[OPS]=−2sin(β/2) 、
[OSQ]=−2sin(β/2) 、[OQA]=2sin(α+β)
なので、
[ABPSQ]=2sinα−4sin(β/2)+2sin(α+β)
=4(sin(α+β/2)cos(β/2)−sin(β/2))
ここで、 α=π/4 、β=π/2 のとき、 [ABPSQ]=0 となるので、
有向でない三角形RABの面積の値と有向でない四角形PSQRの面積の値が等しくなる
場合があることが示された。
(コメント) 多分、この問題を初等幾何で解くことは難しいだろう...。
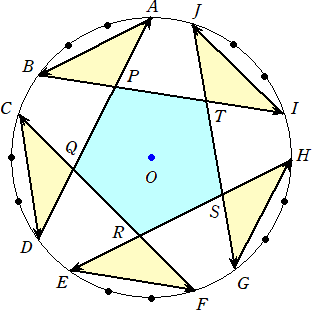
問題 半径2の円Oの周上に、12個の等分点A、B、C、D、E、F、G、H、I、J、K、Lがあ
る。下図のように、辺が交叉する点をそれぞれ P、Q、R とおく。
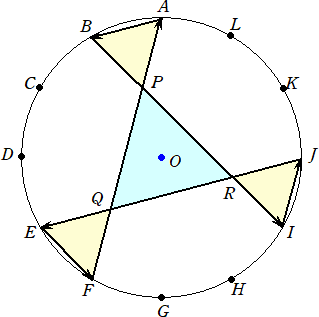
このとき、三角形PQRの面積は、三角形ABPの面積の3倍に等しいことを示せ。
(解) [ABIJEF]=[OAB]+[OBI]+[OIJ]+[OJE]+[OEF]+[OFA] において、
[OAB]=[OIJ]=[OEF]=2sin30°=1
[OBI]=[OJE]=[OFA]=−2sin150°=−1
なので、 [ABIJEF]=0 が成り立つ。
ここで、 [ABIJEF]=[ABP]+[PRQ]+[EFQ]+[IJR]=3*[ABP]+[PRQ] より、
3×(三角形ABPの面積)−(三角形PQRの面積)=0
すなわち、 (三角形PQRの面積)=3×(三角形ABPの面積) が成り立つ。 (終)
同様に、次の問題も解かれる。
問題 半径2の円Oの周上に、8個の等分点A、B、C、D、E、F、G、Hがある。下図のよ
うに、辺が交叉する点をそれぞれ P、Q、R、S とおく。
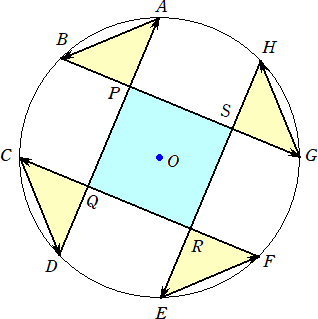
このとき、四角形PQRSの面積は、三角形ABPの面積の4倍に等しいことを示せ。
(解) [ABGHEFCD]=[OAB]+[OBG]+[OGH]+[OHE]
+[OEF]+[OFC]+[OCD]+[ODA]
において、
[OAB]=[OGH]=[OEF]=[OCD]=2sin45°=
[OBG]=[OHE]=[OFC]=[ODA]=−2sin135°=−
なので、 [ABGHEFCD]=0 が成り立つ。
ここで、
[ABGHEFCD]=[ABP]+[PSRQ]+[CDQ]+[EFR]+[GHS]=4*[ABP]+[PSRQ]
より、 4×(三角形ABPの面積)−(四角形PQRSの面積)=0
すなわち、 (三角形PQRSの面積)=4×(三角形ABPの面積) が成り立つ。 (終)
(コメント) 正方形PQRSを対角線で4等分すれば、結果は自明かな...。
問題 半径2の円Oの周上に、20個の等分点がある。下図のように、それらから10個の
点A、B、C、D、E、F、G、H、I、Jを選び、辺が交叉する点を P、Q、R、S、T とおく。
このとき、五角形PQRSTの面積は、三角形ABPの面積の5倍に等しいことを示せ。
(解) [ABIJGHEFCD]=[OAB]+[OBI]+[OIJ]+[OJG]+[OGH]
+[OHE]+[OEF]+[OFC]+[OCD]+[ODA]
において、
[OAB]=[OIJ]=[OGH]=[OEF]=[OCD]=2sin54°
[OBI]=[OJG]=[OHE]=[OFC]=[ODA]=−2sin126°=−2sin54°
なので、 [ABIJGHEFCD]=0 が成り立つ。
ここで、
[ABIJGHEFCD]=[ABP]+[PTSRQ]+[CDQ]+[EFR]+[GHS]+[IJT]
=5*[ABP]+[PTSRQ]
より、 5×(三角形ABPの面積)−(五角形PQRSTの面積)=0
すなわち、 (五角形PQRSTの面積)=5×(三角形ABPの面積) が成り立つ。 (終)
今までの計算をもとに、n個の等分点に関して考察しよう。
問題 半径2の円Oの周上に、等分点A1、A2、・・・、An がある。下図のように、
弧AnAn+1上に、∠AnOBn=α となる点Bnをとり、交叉点をそれぞれCnとおく。

このとき、n角形C1C2・・・Cnの面積が、三角形A1B1C1の面積のn倍に等しいように
nの値を定めよ。
(解) 題意より、[A1B1AnBn・・・A2B2]=n[A1B1C1]+[C1Cn・・・C2]=0
ところで、 [A1B1AnBn・・・A2B2]=n([OA1B1]+[OB2A1])=0 より、
2sinα−2sin(2π/n+α)=0 すなわち、 4cos(π/n+α)sin(π/n)=0
上式を満たすような n と α の組合せは、n≧3として、次の場合に限られる。
(n ,α)=(3 ,π/6) 、(4 ,π/4) 、(5 ,3π/10)
(コメント) n≧6 という場合は、起こり得ないことが分かりました!
問題 △ABCと△PQRにおいて、線分AP、BQ、CRの中点が一致するものとする。
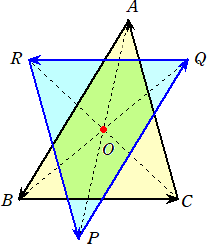
このとき、 △ABC=△PQR であることを示せ。
(解) △ABC=[OAB]+[OBC]+[OCA] 、△PQR=[OPQ]+[OQR]+[ORP]
において、 [OAB]=[OPQ] 、[OBC]=[OQR] 、[OCA]=[ORP] なので、
△ABC=△PQR
が成り立つ。 (終)
(コメント) 一般のn角形S、T(向きは同じ向き)において、頂点を結ぶ線分の中点が一致
するとき、同様に、S=T が成り立つことは明らかだろう。
以下、工事中!



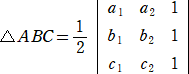

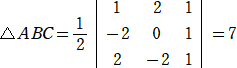
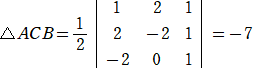 (終)
(終)