ある点の軌跡
 |
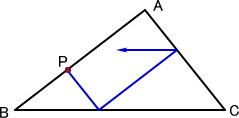
左図のような△ＡＢＣにおいて、辺ＡＢ上の任意の 位置に点Ｐをとる。 いま点Ｐが辺ＡＣに平行に動き、辺ＢＣとぶつかっ たら進路を変更して、今度は辺ＡＢに平行に動く。 辺ＡＣにぶつかったら、さらに進路を変更して、辺 ＢＣに平行に動く。 このように点Ｐは、△ＡＢＣ内を各辺に平行に動き 点Ｐに戻ったら、動きを停止するものとする。 |
最初この問題を見たとき、「点Ｐは、永遠に三角形内を動き続けるのでは？」と思ったが、
「平行」という条件がすこぶる厳しく、意外に、はやく収束するのには驚かされた。
 |
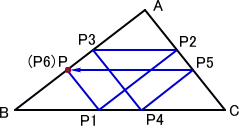結果は、左図の通りで、点Ｐが辺ＡＢの中点でな ければ、辺と ６ 回目にぶつかる時点で、元の点Ｐ にかえる。 （中点の場合は、３回目で元の点にかえる。） （検証） ＡＰ：ＢＰ＝ＣＰ１：ＢＰ１ ＣＰ１：ＢＰ１＝ＣＰ２：ＡＰ２ ＣＰ２：ＡＰ２＝ＢＰ３：ＡＰ３ よって、ＡＰ：ＢＰ＝ＢＰ３：ＡＰ３ |
| 同様にして、ＡＰ３：ＢＰ３＝ＢＰ６：ＡＰ６ なので、ＡＰ：ＢＰ＝ＡＰ６：ＢＰ６ から、Ｐ６＝Ｐ | |
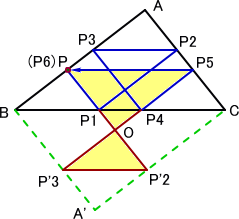上記の比の計算は、左図のように考えれば、分か
りやすいかもしれない。
△ＯＰＰ５∽△ＯＰ'２Ｐ'３ であることが直ちに了
解できるので、確かにＰ６とＰは一致する。
また、点Ｐが元の点にかえるまでに描く軌跡の長
さは、△ＡＢＣ の周の長さに一致するということも、
図から明らかであろう。
（追記） 上記のような問題を、今度は正方形について考えてみよう。上記では、「平行」に
移動したが、正方形の場合は、正方形内を任意の方向に直線的に移動し、正方
形の辺にぶつかったら、反射（入射角と反射角は等しい）により、移動する向きを
変えるものとする。
例えば、次のように移動する。
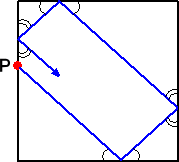
点Ｐ を出発した点が、元の点Ｐ に戻れる確率は、上記の平行移動とは違って、著しく低
いように感じる。事実、その確率は、０ であって、元に戻れたとしたら、それは稀有な偶然
が起こった場合のみである。それ故に、ビリヤードは面白いのだろう。
それでは、元の点に戻れる場合とは、どのような条件を満たす場合であろうか？
一つ例示をして、考えてみよう。
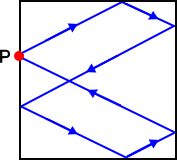
上図の場合、５回反射して、元の点 Ｐ に戻っているが、その状況を詳しく分析すると、次
のようになっているものと考えてよい。
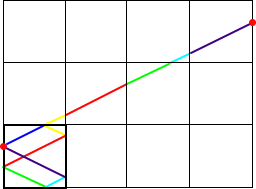
すなわち、上記のような格子を考え、点Ｐと同様な位置にある２点を結ぶ直線上を移動す
る場合のみ、元の点 Ｐ に戻る。
このように考えると、元の点に戻る条件は、直線の傾きが有理数ということになる。
したがって、実数全体に対して、有理数の個数は少ない（？）（＝測度が０）ので、元に戻る
確率は、０ である。しかし、有理数自体は無限個あるので、元に戻る場合は、たくさん起こ
り得る。ここら辺は、確率が「０」という認識と微妙なズレがあって、面白い。
（参考文献：栗田 稔 著 問題はどう作られるか （東京出版））
（追記） 令和７年９月１３日付け
次の東北大学 前期理系（１９９９）の問題は、上記の趣旨の問題である。
問題 長方形ＡＢＣＤ内を減速しながら進む点を考える。時刻 ｔ＝０ に初速ｖで発射させた
点Ｐは、時刻 ｔ では速さｖｅ-tで直進するとする。ただし、Ｐがいずれかの辺に来たときは
等しい入射角と反射角で反射するとし、頂点Ａ、Ｂ、Ｃ、Ｄのいずれかに来たときは、そこ
で停止するとする。ＡＢの長さは４でＡＤの長さは２とし、出発点はＡＤの中点Ｏとする。初
速をｖ＝１４としたとき、最も長い時間をかけてＰをどれかの頂点に到達させるにはどの
方向に発射させればよいか。ＯＡとの角をθ(０＜θ＜π/２）として、ｔａｎθを求めよ。
また、そのとき、Ｐが頂点に到達する時刻を求めよ。
（解） 長方形ＡＢＣＤを横方向にｍ枚、縦方向にｎ枚用意し、初めて光が頂点に到達したもの
とする。
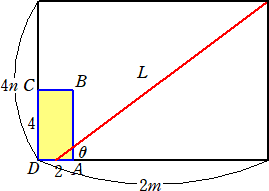
Ｐが頂点に到達するまでの時間をＴとして、その道のりＬは、
Ｌ＝∫0T １４ｅ-tｄｔ＝１４[−ｅ-t]0T＝１４（１−ｅ-T）
このとき、 Ｌ2＝（２ｍ−１）2＋（４ｎ）2＜１４2＝１９６ から、 ｎ＝１、２、３
ｎ＝１ のとき、 （２ｍ−１）2＜１９６−１６＝１８０ から、 ｍ＝１、２、・・・、７ で、
ｍ＝７ のときＬは最長で、 Ｌ2＝１３2＋４2＝１８５
ｎ＝２ のとき、 （２ｍ−１）2＜１９６−６４＝１３２ から、 ｍ＝１、２、・・・、６ で、
ｍ＝６ のときＬは最長で、 Ｌ2＝１１2＋８2＝１８５
ｎ＝３ のとき、 （２ｍ−１）2＜１９６−１４４＝５２ から、 ｍ＝１、２、３、４ で、
ｍ＝４ のときＬは最長で、 Ｌ2＝７2＋１２2＝１９３
以上から、最も長い時間をかけてＰをどれかの頂点に到達させるには、長方形ＡＢＣＤを
横方向に４枚、縦方向に３枚用意すればよい。そのとき、到達する頂点は、Ｃである。
このとき、 ｔａｎθ＝１２/７ である。
また、 １４（１−ｅ-T）＝√１９３ より、 Ｔ＝−ｌｏｇ（１−（√１９３）/１４） （終）
以下、工事中！