
 |
大相撲千秋楽で同点決勝になった場合、よく行われる試合 形式が「巴戦」である。必ず決着をつけようという日本独特の 文化の賜物であろう。 サッカーJリーグでも、欧州にはない独自の「延長Vゴール方 式」というものを編み出したし、甲子園の高校野球でも、延長 18回で決着がつかなければ翌日再試合という、高校生にとっ て体力的に厳しいシステムになっている。 私たちの記憶に残る名場面も、なぜかそういう規定外でのも のが多い。日本の文化にどっぷり浸かっている証しでもある。 その点、ラグビーは、ノーサイドとともに、同点優勝がありうる。 正規の試合の中で、決着がつかなければ、両者優勝という考え 方は、清々しい。 |
Jリーグでは来季から延長Vゴール方式がなくなるようだ。高校野球でも、将来の大器を潰
さないためにも、9回までの勝負に徹するべきだと思う。
このページでは、「巴戦」の数理について調べ、その不平等さを記録として残しておきたい。
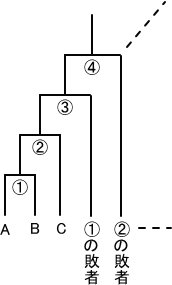
3人 A、B、C による勝ち抜き戦(巴戦)は、上図のような対戦方式により行われる。初めて
2連勝する人が出現するまで、上記の対戦は続く。
A、B、C の実力は互角とする。このとき、それぞれの優勝する確率は、実は等しくない。実
力が互角であっても、最初に対戦する2人(AとB)の方が優勝する確率は高い。これは、注目
すべき事実である。
従って、Cに入った人は、多少不利であることを自覚しなければならない。このような不平等
な試合形式で優勝者を決めるというやり方は、是非、止めた方がよい。
A、B、C の優勝する確率を、それぞれ P(A)、P(B)、P(C) とおく。対戦方式の特性から、
P(A)=P(B) で、P(C)=1− P(A)−P(B)
最初の対戦で A が勝つ事象を、a とすると、
P(A)=P(a)Pa(A)+P(ac)Pac(A)=(1/2)Pa(A)+(1/2)Pac(A)
である。ただし、ac は a の余事象とする。
優勝が決まるまでは毎回、対戦終了後、3人は次の3つのタイプのいずれかに分類される。
X : 直前回の対戦で勝った人
Y : 直前回の対戦で負けた人
Z : 直前回の対戦で控えだった人
今、X、Y、Zの人が優勝する事象を、それぞれ E、F、G とする。
毎回 X と Z が対戦する。X が勝つ事象を、x とする。このとき、
P(E)=P(x)Px(E)+P(xc)Pxc(E)=(1/2)Px(E)+(1/2)Pxc(E)
P(F)=P(x)Px(F)+P(xc)Pxc(F)=(1/2)Px(F)+(1/2)Pxc(F)
P(G)=P(x)Px(G)+P(xc)Pxc(G)=(1/2)Px(G)+(1/2)Pxc(G)
ここで、Xは直前回の対戦で勝っているので、Px(E)=1、Px(F)=Px(G)=0 が成り立つ。
他方、Xが負けたという場合(事象としては、xc)において、XはYに、YはZに、ZはXに立場
が変わるので、
Pxc(E)=P(F)、 Pxc(F)=P(G)、 Pxc(G)=P(E)
が成り立つ。これらを、上記の3式に代入して、
P(E)=(1/2)+(1/2)P(F)
P(F)=(1/2)P(G)
P(G)=(1/2)P(E)
よって、P(E)=4/7、P(F)=1/7、P(G)=2/7 となる。
ところで、E、F の定義から、明らかに、Pa(A)=P(E)、Pac(A)=P(F) が成り立つので、
P(A)=(1/2)P(E)+(1/2)P(F)=5/14
同様にして、 P(B)=5/14、 P(C)=4/14 が成り立つ。
(別解) 今、機会があって上記解答を眺めていると、その煩雑さに気が滅入る。決して
難しいことを述べてはいないが、一般の方向けとはいい難い。次のように解答を
整理してみた。
A、B、C の3人のうちの2人甲と乙が対戦し、甲が勝ったときに乙が優勝する
確率をPとおく。まず、Aが優勝する確率は、
BとCに勝つとき ・・・・・ 1/2×1/2=1/4
Bに勝ってCに負けるとき ・・・・・ 1/2×1/2×P=P/4
Bに負けるとき ・・・・・ 1/2×P=P/2
より、 1/4+P/4+P/2=1/4+3P/4
Bが優勝する確率は、Aと同じで、1/4+3P/4
Cが優勝する確率は、
AとBに勝つとき ・・・・・ 1/2×1/2=1/4
AとBのどちらかに勝って、他方に負けるとき ・・・・・ 1/2×1/2×P=P/4
より、 1/4+P/4
したがって、(1/4+3P/4)+(1/4+3P/4)+(1/4+P/4)=1 より、
7P/4=1/4 すなわち、P=1/7
これから A、B、C が優勝する確率は、それぞれ 5/14、5/14、4/14 となる。
(別解証明 終)
(追記) 平成29年9月1日付け
直接的に次のようにも計算できる。
P(A)=(1/22+1/25+・・・)+(1/24+1/27+・・・)=5/14
同様に、P(B)=5/14 なので、P(C)=4/14
このように巴戦の場合、最初に取り組む2人が他の一人よりも絶対的に有利である。
A、B、Cの強さが同じと仮定するとき、優勝が決まるまでの取組数の期待値は、
2取組で優勝が決まる確率 1/22+1/22=1/2
3取組で優勝が決まる確率 1/23+1/23=1/4
4取組で優勝が決まる確率 1/24+1/24=1/8
・・・・・・・・・・・・・・・・・・
なので、 S=2×(1/2)+3×(1/4)+4×(1/8)+・・・・ とおくと、
2S=2+3×(1/2)+4×(1/4)+・・・・ より、
S=2+(1/2)+(1/4)+・・・・=2+(1/2)/(1−1/2)=3
無限に取組が続きそうであるが、取組数の期待値は意外に小さく、3回である。
初めの取組でAがBに勝ったとすると、A、B、Cの優勝する確率は、それぞれ
4/7、1/7、2/7
となる。
私の記憶するところによれば、この「巴戦」を題材に出題された大学入試問題は、昭和61
年度入試の神戸大学(理系)が最初ではないだろうか。次のような問題であった。
A、B、C の3人で勝ち抜き戦を行う。3人の戦力は同等である。第1回戦で、AとBが対戦
し、その勝者が第2回戦でCと対戦する。もし、Cが負ければ、AかBが連勝したことになり、
優勝が決まるものとする。もし、Cが勝てば、第1回戦の敗者が第3回戦でCと対戦する。以
下これを繰り返し、誰かが2連勝したところで優勝が決まるものとする。このとき、次の各問
に答えよ。
(1)第1回戦でBが勝ち、第2回戦でCが勝ち、第3回戦ではAが勝った場合を、BCA
のよう
に表すことにする。このような表し方で、第1回戦から第7回戦までにAが優勝する場合を
全て書け。
(2)第n回線までに優勝が決まらない確率を求めよ。
(3)第n回線までに、Cが優勝する確率を Pn とするとき、lim Pn の値を求めよ。
問題の難易度レベルとしては、標準程度である。
答は、(1) AA、ACBAA、BCAA、BCABCAA の4通り
(2) (1/2)n−1
(3) P3k=P3k+1=P3k+2=(2/7)(1−(1/8)n) より、lim Pn=2/7
実際の計算は、読者のための練習問題として残しておこう。
(参考文献:玉置光司 著 基本確率(牧野書店))
この話題の関連として、当HPがいつもお世話になっているHN「GAI」さんから、「七人の侍
と選抜野球大会」と題して、ご投稿いただいた。(平成28年1月9日付け)
七人の侍が最強を決めるため、剣道によるリーグ戦を実施した。実力伯仲のため、特定
の3人では三つ巴状態(三竦み)が起こったりもした。すべての試合では引き分けはないも
のとして、7C3=35(組)中、三竦みは最大いくつ起き得るか?
また、甲子園での選抜高等学校野球大会(参加校32校)を、トーナメントからリーグ戦に
て戦った場合、引き分けが起こらないとして、32C3=4960(組)中、三竦みが最大いくつ起
き得るか?
らすかるさんからのコメントです。(平成28年1月10日付け)
適当にプログラムを作って調べただけですが、「A006918」のようですね。つまり、7人なら、
最大35組中14組、32校なら、最大4960組中1360組。
GAI さんからのコメントです。(平成28年1月10日付け)
一般に、n人が参加するリーグ戦では「三竦み」が起こり得る最大数a(n)は、
nが奇数のとき、 a(n)=(n-1)*n*(n+1)/24
nが偶数のとき、 a(n)=(n-2)*n*(n+2)/24
と、微妙に奇数と偶数では異なることになるんですね。適当にプログラムを組めば、この数列
を導けるとは羨ましいです。
私は手作業で6人の場合まで三竦みを拾い上げ(約半日を要す。)やっとこのものに辿り着
きました。しかし、Sloane氏の整数列大辞典には、どんなタイプの問題の解答も載せてあるも
のです。(いい仕事してますね。)
(コメント) 4人が参加するリーグ戦では「三竦み」が起こり得る最大数a(n)は、公式によれ
ば、 a(4)=(4-2)*4*(4+2)/24=2 となるんですね。
Bruno Berselli(2011)さんの結果を参考に、GAI さんの2つの場合を一つにま
とめると、 a(n)=n(2(n-2)(n+2)-3(-1)n+3)/48 となるようです。
at さんからのコメントです。(平成28年6月17日付け)
興味深い問題ですね。この「七人の侍と選抜野球大会」問題は、2004年 ポーランド数学オ
リンピックのファイナルラウンドでも出題された問題のようです。参考までに。