
いろいろな関数を、整級数で表すひとつの方法として、Taylor展開がある。この展開は、
平均値の定理の一般化である「Taylorの定理」から得られる。
Taylor展開そのものは単純であるが、その力は絶大である。近似式の計算など活躍する
場は多い。私が高校時代に、この展開を知って一番感動的だったのは、極限値の計算に
おいてである。
例 次の極限値を求めよ。
![]()
この極限値は、ロピタル(de l’Hospital)の定理を用いると、次のように計算される。
![]()
ところが、関数 sin X の X=0 におけるTaylor展開
![]()
を知っていれば、上記の極限値の計算は、難しい計算をしなくても即答できる。
(追記) 当HPの掲示板「出会いの泉」に、平成24年2月15日付けで、HN「ethanhunt」さ
んが質問を書き込まれた。
| テーラー展開を勉強中のものです。 | |
が、テイラー展開により、 |
簡明にわかるとのことですが、いったいどう考えれば”簡明”にわかりますか?
当HPがいつもお世話になっているHN「空舟」さんにご回答いただきました。
(平成24年2月15日付け)
テイラー展開により、
![]()
ランダウの記号を使うと、 sinx=x−x3/6+o(x3) と書けます。このo(x3)の意味
は、x3 より速く0に収束する(x3 より高位の無限小)という意味です。すなわち、
sinx=x−x3/6+R(x) とすると、limx→0 (R(x)/x3)=0 という意味です。
これらが成り立つことを主張するのがテイラーの定理ですが、その証明はどこか
で学習してもらうとして省略します。
(x-sinx) / x3=[ x-{x-x3/6+o(x3)} ] / x3=1/6 + (o(x3)/ x3) → 1/6
...こんな感じでしょうか。
(コメント) ランダウの記号を持ち出さなくても、
(x−sinx)/x3=1/6+x2/24+・・・ から、軽い気持ちで、x → 0 のとき、
1/6 に収束するという...雰囲気デス!
また、Taylor展開は、その関数の持っている性質を如実に物語ってくれる。
例 (ex)’=ex という美しい関係式は、ex の X=0 におけるTaylor展開
![]()
を見れば、ほとんど明らかである。
このように、Taylor展開の利用価値は高いが、逆に、ある関数をTaylor展開しようとする
場合、幾ばくかの困難を伴う。
第 n 次導関数が簡単に類推できる場合はいいのだが、そうでない場合は、どうしたらいい
のだろうか。
いろいろな工夫が知られているが、微分方程式を利用したTaylor展開の方法がとてもエレ
ガントであると思う。九州大学大学院の入試問題(改題)を参考に、その求め方を見てみよう。
問題 次の関数の X=0 におけるTaylor展開を求めよ。
![]()
(解)
![]()
であることから、
(1+X2)f’(X)+X・f(X) = 0
という微分方程式が得られる。
この式の両辺を n 回微分すると、Leibniz の定理より、
(1+X2)f(n+1)(X)+(2n+1)X・f(n)(X)+n2・f(n-1)(X) = 0
ここで、X=0 を代入して、
f(n+1)(0)+n2・f(n-1)(0) = 0
となる。ここで、f(0)=1、f’(0)=0 であることに注意して、上の漸化式より、
n =2k+1 のとき、 f(2k+1)(0)=0
n =2k のとき、 f(2k)(0)=−(2k−1)2・f(2k-2)(0)
=・・・・・・・・・・・・・・・・・・・・・
=(−1)k(2k−1)2(2k−3)2・・・32・12
ただし、k≧1 の自然数とする。
(厳密には、数学的帰納法による証明が必要である。)
したがって、
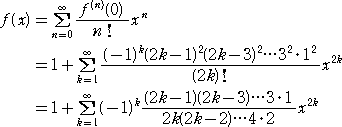
が求めるTaylor展開となる。
簡単な計算から、この級数の収束半径は、1 であることが分かる。