
丂僄儕丒儅僆乕儖挊丗乽慺惏傜偟偄嶰妏朄偺悽奅乿乮岲揷弴帯栿丂惵搚幮姧乯傪撉傫偱偄偨傜丄
偲偰傕巋寖揑側堦暥偵憳嬾偟偨丅
丂奜尒偼堈偟偦偆偵尒偊傞偑丄偦偺徹柧偼宱尡偺偁傞幚慔幰偨偪偵偝偊暘偐傜側偄
偙偲偑偁傞丅
偦傟偼丄椺偊偽丄師偺傛偆側栤戣偱偁傞丅
丂擟堄偺嶰妏宍偵偍偄偰丄俀偮偺撪妏偺俀摍暘慄偺挿偝偑摍偟偗傟偽丄偦偺嶰妏宍
偼丄擇摍曈嶰妏宍偱偁傞偙偲傪徹柧偣傛丅
丂偙傟偼丄妏偲慄暘偺娫偺娭學傪栤偆栤戣偱丄偦偺娭學偼丄娙扨偲偼偲偰傕尵偊側偄偲偄偆
堦偮偺椺傪梌偊偰偄傞丅壗擔娫偐丄徹柧傪偟偰傒傛偆偲帋傒偨偑丄偆傑偔偄偐側偐偭偨丅
丂偦傫側偲偒丄峀搰岺嬈戝妛偺戝愳尋媶幒偐傜丄
丂乽偙偺帠幚偼丄Steiner-Lehmus Theorem 偁傞偄偼 Lehmus' Theorem 側偳偲偄傢
丂傟丄桳柤側掕棟偱偁傞丅乿
偲丄偛嫵帵傪偄偨偩偒丄偝傜偵丄師偺傛偆側儂乕儉儁乕僕傑偱専嶕偟偰偄偨偩偄偨丅
偙偺儁乕僕偺嶌惉偵偁偨傝丄戝偄偵嶲峫偵側傝傑偟偨丅戝愳尋媶幒偵丄姶幱偄偨偟傑偡丅
丒丂http://www.mathforum.com/epigone/geometry-college/clanflarblax
/Pine.LNX.4.10.10006221025190.11559-100000@dl2sql9.princeton.edu
丒丂http://www.mathematik.uni-bielefeld.de/~sillke/PUZZLES/steiner-lehmus
丒丂http://www.math.niu.edu/~rusin/known-math/99/steiner-lehmus
丂偙傟傜偺儂乕儉儁乕僕偵傛傞偲丄偙偺掕棟偵娭偟偰偼丄俇侽庬椶埲忋偺徹柧偑抦傜傟偰偄
傞偲偺偙偲偱偁傞丅乮俛倝倢倢丂俲倢倕倝値倛倎値倱丂偵傛傞乯
丂偦傟傜偺拞偐傜丄巹揑偵岲偒側丄崅峑惗偱傕棟夝偱偒傞暯堈側徹柧傪徯夘偟偨偄偲巚偆丅
徹柧乮侾乯
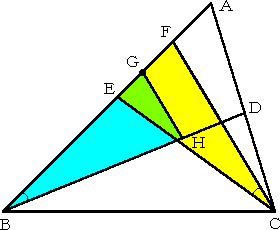 丂丂仮俙俛俠偵偍偄偰丄佢俛亙佢俠丂偲偡傞丅佢俛丄
丂丂仮俙俛俠偵偍偄偰丄佢俛亙佢俠丂偲偡傞丅佢俛丄丂佢俠 偺俀摍暘慄傪丄BD丄俠俤 偲偟丄慄暘俙俤忋
丂偵揰俥傪丄佢俙俛俢亖佢俤俠俥 偲側傞傛偆偵偲傞丅
丂偝傜偵丄佢俛亙佢俛俠俥 傛傝丄曈俛俥忋偵揰俧傪丄
丂BG亖俠俥 偱偁傞傛偆偵偲傟傞丅傑偨丄慄暘俛俢
丂忋偵揰俫傪丄GH偲俥俠偑暯峴偲側傞傛偆偵偲傞丅
丂丂偙偺偲偒丄柧傜偐偵丄
丂丂丂丂丂丂丂丂丂仮俛俧俫佭仮俠俥俤
丂偑惉傝棫偮丅傛偭偰丄丂俠俤亖俛俫丂偑偄偊傞丅
丂俛俫亙俛俢丂側偺偱丄偟偨偑偭偰丄
丂丂丂丂丂佢俛亙佢俠丂側傜偽丄俠俤亙俛俢
丂摨條偵偟偰丄
丂丂丂丂丂佢俛亜佢俠丂側傜偽丄俠俤亜俛俢
丂偟偨偑偭偰丄傕偟丄俠俤亖俛俢丂偑惉傝棫偮側傜偽丄佢俛亖佢俠丂偡側傢偪丄仮俙俛俠丂偼丄擇
摍曈嶰妏宍埲奜偵偁傝偊側偄丅
乮拲乯丂婔壗偺徹柧傜偟偔丄岻柇側庤弴偱徹柧偝傟偰偄傞丅偲偰傕丄姶摦揑偩両
丂丂丂偙偺傛偆側徹柧曽朄傪丄揮姺朄偲偄偆丅
徹柧乮俀乯丂丒丒丒丂嶰妏娭悢傪梡偄偨夝朄
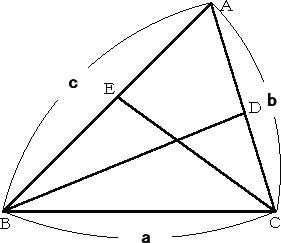 丂丂仮俙俛俠偵偍偄偰丄佢俛亙佢俠丂偲偡傞丅
丂丂仮俙俛俠偵偍偄偰丄佢俛亙佢俠丂偲偡傞丅丂佢俛亖俀兤丄佢C亖俀冇丂偲偍偔丅
丂丂仮俙俛俠亖仮俙俛俢亄仮俛俠俢丂側偺偱丄
丂丂俀仮俙俛俠亖們丒俛俢倱倝値兤亄倎丒俛俢倱倝値兤
丂丂丂丂丂丂丂丂亖乮們亄倎乯俛俢倱倝値兤
丂丂摨條偵偟偰丄
丂丂仮俙俛俠亖仮俠俙俤亄仮俠俛俤丂側偺偱丄
丂丂俀仮俙俛俠亖倐丒俠俤倱倝値冇亄倎丒俠俤倱倝値冇
丂丂丂丂丂丂丂丂亖乮倎亄倐乯俠俤倱倝値冇
丂丂偙偺偙偲偲丄俛俢亖俠俤丂偐傜丄
丂丂丂丂丂乮們亄倎乯倱倝値兤亖乮倎亄倐乯倱倝値冇
丂丂偡側傢偪丄
丂丂丂們丒倱倝値兤亅倐丒倱倝値冇亖倎乮倱倝値冇亅倱倝値兤乯
丂丂侽亱亙兤亙冇亙俋侽亱側偺偱丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂倱倝値冇亜倱倝値兤丂偐傜丄倱倝値冇亅倱倝値兤亜侽丂偑惉傝棫偮丅
丂傛偭偰丄們丒倱倝値兤亅倐丒倱倝値冇亜侽丂偡側傢偪丄們丒倱倝値兤亜倐丒倱倝値冇亜侽丂偲側傞丅
偲偙傠偱丄侽亱亙兤亙冇亙俋侽亱偺偲偒丄們倧倱兤亜們倧倱冇亜侽丂側偺偱丄俀偮偺晄摍幃傪丄曈乆偐
偗偰丄丂們丒倱倝値兤們倧倱兤亜倐丒倱倝値冇們倧倱冇丂丂偐傜丄俀們丒倱倝値兤們倧倱兤亜俀倐丒倱倝値冇們倧倱冇丂偱丄
偡側傢偪丄們丒倱倝値俛亜倐丒倱倝値俠丂偲側傞丅偙傟偼丄們丒倱倝値俛亖倐丒倱倝値俠丂偱偁傞偙偲偵柕弬偡傞丅
摨條偵偟偰丄佢俛亜佢俠丂偲偟偰傕柕弬傪摼傞偺偱丄俛俢亖俠俤丂側傜偽丄佢俛亖佢俠丂偱偁傞丅
偟偨偑偭偰丄仮俙俛俠丂偼丄擇摍曈嶰妏宍偲側傜側偗傟偽側傜側偄丅
乮拲乯丂悢妛嘦掱搙偺嶰妏娭悢偺抦幆偑梡偄傜傟偰偄傞偑丄屻敿晹暘偺榑棟偺揥奐偺忋
丂丂丂庤偝偵偼姶怱偣偞傞傪偊側偄丅
乮捛婰乯丂彮偟嫮堷偱偼偁傞偑丄捈愙揑偵寁嶼偱媮傔傞曽朄傕抦傜傟偰偄傞丅
徹柧乮俁乯丂丒丒丒丂僿儘儞偺岞幃傪梡偄偨夝朄
 丂丂丂俛俢 偲 俠俤 傪偦傟偧傟佢俛丄佢俠 偺擇摍暘
丂丂丂俛俢 偲 俠俤 傪偦傟偧傟佢俛丄佢俠 偺擇摍暘丂丂慄偲偡傞丅壖掕傛傝丄俛俢 亖 俠俤 偱偁傞丅
丂丂丂佢俛亖俀兤 偲偍偔偲丄
丂丂丂仮俙俛俠亖仮俙俛俢亄仮俛俠俢丂側偺偱丄
丂丂丂俀仮俙俛俠亖們丒俛俢倱倝値兤亄倎丒俛俢倱倝値兤
丂丂丂丂丂丂丂丂 亖乮們亄倎乯俛俢倱倝値兤
丂丂丂偲偙傠偱丄僿儘儞偺岞幃傛傝丄
丂丂丂丂仮俙俛俠亖
丂丂丂偑惉傝棫偮丅
丂丂丂丂偨偩偟丄
丂丂丂丂丂丂丂丂
丂丂丂偲偡傞丅
丂傑偨丄嶰妏娭悢偺敿妏偺岞幃傛傝丄
丂丂丂丂丂丂丂丂丂丂丂丂丂
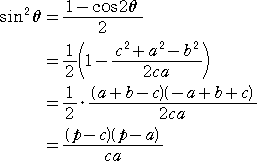
側偺偱丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂
偙傟傜傪丄俀仮俙俛俠亖乮們亄倎乯俛俢倱倝値兤丂偵戙擖偟偰丄俛俢 傪夝偔偲丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
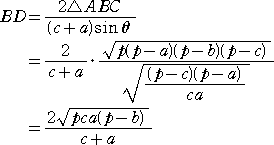
摨條偵偟偰丄
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
俛俢 亖 俠俤丂偡側傢偪丄俛俢2 亖 俠俤2丂偵忋幃傪戙擖偟偰幃傪惍棟偡傞偲丄
丂丂丂丂丂們乮倎亄倐乯2乮倎亅倐亄們乯亖倐乮們亄倎乯2乮倎亄倐亅們乯
偙偺幃傪揥奐偟偰丄
丂丂丂丂丂們倐3亄乮倎2亄俁們倎乯倐2亄乮倎3亅俁們2倎亅們3乯倐亅們倎3亅們2倎2亖侽
倐 偺曽掱幃偲尒偰丄倐 偵 們 傪戙擖偡傞偲丄嵍曈亖侽丂偵側傞偺偱丄場悢掕棟偵傛傝丄嵍曈偼丄
倐亅們 偱妱傝愗傟傞丅傛偭偰丄嵍曈偼場悢暘夝偝傟偰丄
丂丂丂丂丂丂丂丂丂丂乮倐亅們)(們倐2亄乮倎2亄俁們倎亄們2乯倐亄倎3亄們倎2乯亖侽
偙偙偱丄倎丄倐丄們 偼丄惓偺悢側偺偱丄們倐2亄乮倎2亄俁們倎亄們2乯倐亄倎3亄們倎2亗侽丂偱偁傞丅
傛偭偰丄倐亅們亖侽丄偡側傢偪丄倐亖們丂偱丄仮俙俛俠 偼丄擇摍曈嶰妏宍偲側傞丅
乮拲乯丂悢妛嘥掱搙偺嶰妏娭悢偺抦幆丄偍傛傃悢妛俛偵偍偗傞曽掱幃偺棟榑乮怴妛廗巜摫
丂丂丂梫椞偱偼丄悢妛嘦乯偑梡偄傜傟偰偄傞偑丄寁嶼偼丄憡摉僴乕僪偱偁傞丅惓捈偵崘敀偡傞
丂丂丂偲丄巹帺恎丄寁嶼儈僗傪壗搙偐宱尡偟偨丅
乮捛婰乯丂暯惉俀係擭俀寧侾俆擔晅偗
丂嬻廙偝傫傛傝丄Steiner-Lehmus Theorem 偺徹柧偵偮偄偰丄嶲峫僒僀僩傪偛徯夘偄偨偩
偒傑偟偨丅