
スーパーなどで、大きさの決まった袋が用意されていて、それに詰めるだけ詰めて定額
料金というのが「大安売りセール」の定番メニューになっている。
事前に袋を力一杯拡げて、まず容積を増やそうと考えるのが常道だが、得てして用意さ
れた袋がのびない材質のものである場合が多く、そういった努力はただ空しく水泡に帰す
るだけである。
当HPの投稿コーナーにある「梨の選択 」を読んでも分かる通り、詰め放題だと、できる
だけ隙間を減らそうと思って、小振りのものを選んでギューギュー詰めがちだが、ちょっと
数が少なくなっても大きめのものを選んで詰めた方がお得の場合がある。ここはもうスー
パーの店長さんとの知恵比べであろう。
このページでは、どういう詰め方をすれば最も効率がいいのか、少し検討してみようと思
う。
煙草などは次のようにパッケージされている。
この詰め方はある意味で美しいが、決してお得な詰め方ではない。
詰め方の方法として、次の2つ場合を考えよう。
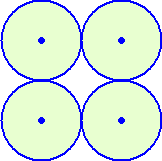
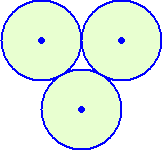
左図の場合は、正方形の構図にがっちり組まれているが隙間が多く発生している。それ
に対して、右図の場合は、三角形の構図にがっちり組まれていて図形として安定している。
しかも、隙間の発生も多少抑えられているように感じる。
左図に対して、右図の組み方がどれくらいの効果があるのか計算してみよう。
下図のように、幅 4 の2直線間に半径 1 の円を配置する。2点AB間がちょうど1周期分
に相当し、円6個分が並べられている。
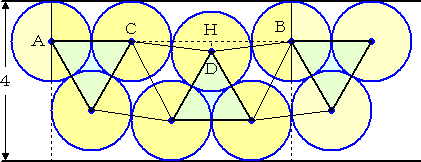
正方形の構図に組んだ場合、円6個分を並べた場合の1周期分の長さは、6 である。
三角形の構図に組んだ場合の 1周期分の長さを求めることにより、その効果をはかる
ことができる。
上図において、DH=2−
CH2=CD2−DH2=4−(2−
よって、 AB=AC+2CH=2+2
小数で表せば、 AB=5.96393906627007・・・ である。
したがって、 99.3989844378345・・・(%)の縮小率となっている。
ほんの僅かの差であるが、「塵も積もれば山となる」と言われるように、たとえば、60周
期分の長さを求めると、
357.836343976204・・・
となって、正方形の構図に組んだ場合の60周期分の長さ 360 と比較して、その差が
2.16365602379579・・・ あることから、もう1個の円が配置され得ることが分かる。
つまり、4×360 の長方形に半径 1 の円を隙間なく並べようとした場合、常識的に考え
ると 360個しか円が配置できないと思われるが、配置の仕方を工夫すると実は、361個
の円を配置することが可能であることが分かったわけである。
これは、何て素晴らしい配置なのだろう!
(でも、60周期分というのは、あまりにも現実的ではないですね。やはり、一般消費者はスーパーの
店長さんの企みに騙されるしかないのでしょうか?)
上記では、三角形の構図を用いて効率的な配置方法を考えたが、さらに効率的な配置
方法というものはないのだろうか? これについては今後の研究課題としよう。
なお、2×1000の長方形に直径1の円を隙間なく並べる場合、2011個の円が並べら
れることが知られている。(Bell 研究所数理科学センター長のグラハム博士が発見)
普通に並べて2000個と思いきや、11個も余計に並べられ得るということは驚きです。
でも、上記の考察を理解すれば、「できそう!」と思えてくるから不思議ですね。
さらに驚くべきことに、ハンガリー学士院のフュレディ博士により、
どのような配置方法をとっても、2013個以上の円を並べることはできない
ということが証明されているらしい。
果たして並べうる最大個数は、2011枚なのか2012枚なのか、どっちだろう?
これについて、もう決着したのだろうか? 何か情報をご存じの方、こちらまでご教示い
ただけたら幸いです。
(追記) 平成20年10月10日付け(←以前だったら「体育の日」で祝日だったのに...!)
HN「GAI」さんが、当HPの掲示板「出会いの泉」に次のような話題を提供された。
10円玉を、10×10個(計100個)の正方形状にまず並べる。これで決まる領域を固定
する。この領域の中に、さらに10円玉を一個追加して計101個のコインを並べるには、ど
んな並びにすればいいだろうか。さらに、あと一個10円玉を追加して計102個のコインを
領域内に収まるようにするには、どう並びをかえれば可能かを挑戦してみて下さい。
この話題は割と有名で、いろいろなHPで取り上げられているようである。
当HPがいつもお世話になっている未菜実さんからの情報によれば、10×10の正方形
には、106個まで入れることができるとのことである。(平成20年10月9日付け)
さらに、未菜実さんから、HP「Circles in Squares」が紹介された。そこには、ある個数を
入れることのできる正方形の最小サイズが24個まで示されているそうである。
10×10の正方形に埋まった106個の円がどんな風に並ぶのか大いに興味があったの
で、下図のように描いてみた。それほど特殊な考えもなく、すんなり106個が収まってくれ
たのには、逆な意味で驚きですね!
