紐をたたむ　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　ここに長さが十分ある１本の紐がある。この紐の真ん中をハサミで切れば、２本に分かれ
る。同様に、１本の紐の両端を揃えてたたみ、その真ん中をハサミで切れば、３本に分かれ
る。ここまでは頭の中に紐の状態をイメージしてもらえれば合点がいくだろう。

　そこで、問題です。

　１本の紐の両端を揃えてたたみ、さらに、その両端を揃えてたたむ。その真ん中をハサミ
で切れば、紐は何本に分かれるだろうか？答えは、５本となる。出来ました？

　さらに問題は続きます。

　１本の紐の両端を揃えてたたみ、さらに、その両端を揃えてたたむ。さらに、その両端を揃
えてたたむ。その真ん中をハサミで切れば、紐は何本に分かれるだろうか？

　ここまでくると、想像するのが大変かも．．．。

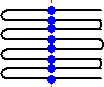
　これまでの操作を図示してみると、規則性が見えてくる。

　すなわち、紐を１回たたむ毎に折り目の点（青色の点）が倍々に増え、そのときの紐の分
割数は折り目の点（青色の点）の個数に１を加えればよい。この最後に１を加えるという感
覚は小学校で学ぶ植木算と同じだ。

　図からも分かるように、上記の問題の答えは、「９本に分かれる」となる。

　以上から、折り目の点（青色の点）の個数は、１回たたむと２、２回たたむと４、３回たたむ
と８、・・・　なので、ｎ回たたむと２^ｎとなる。

　従って、１本の紐をｎ回たたみ、その真ん中をハサミで切れば紐は、２^ｎ＋１本に分かれる
ことが分かる。


（参考文献：朝日新聞　８月４日付け朝刊　花まる先生公開授業　３００回記念）