
今、ある作品を完成させるのに、いくつかの途中工程が必要で、それぞれの作業に要する
日数があらかじめ分かっているものとする。また、それぞれの工程では、事前に終了すべき
工程も指定されている。これらをまとめたものが、次の作業工程一覧である。
スケジュール問題 
今、ある作品を完成させるのに、いくつかの途中工程が必要で、それぞれの作業に要する
日数があらかじめ分かっているものとする。また、それぞれの工程では、事前に終了すべき
工程も指定されている。これらをまとめたものが、次の作業工程一覧である。
| 作業工程 | A | B | C | D | E | F | G | H | I | J | K |
| 先行作業 | なし | A | A | B | C | C | D,E | F | F | G,H | I,J |
| 所要日数 | 1 | 2 | 3 | 1 | 1 | 3 | 2 | 1 | 2 | 2 | 2 |
この作業工程をみて最低何日あれば作品が完成するのかを考えるのが、スケジュール問
題といわれているものである。もちろん、作業は共同作業で、作業工程の同時進行は可能と
する。
ただし、先行作業工程が終了しなければ、その作業工程には取りかかれないものとする。
(一人で全工程を作業する場合、完成に要する日数は各工程の所要日数の和20日となる。)
このような問題は、合理的なプランニングを行い、スケジュールをうまく組まなければなら
ない研究開発のプロジェクトや土木建築工事の工程管理などでよく扱われる。
このスケジュール問題に対して、
PERT(Program Evaluation and Review Technique)
という手法が知られている。(この手法は、米国海軍により開発された。)
PERT法により、次のような矢線図が得られる。作品は、12日で完成することが分かる。
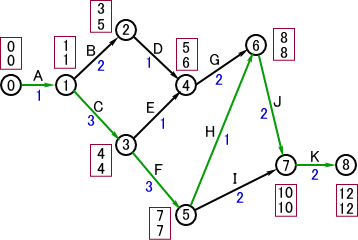
左図において、
青字は各工程の所要日数
赤枠線の上段の数は、
最も早い工程終了日
赤枠線の下段の数は、
最も遅い工程終了日
である。
赤枠線内の数の記入方法
0に各工程の所要日数を順次加えていき、その数を上段に記入する。
ただし、作業の合流地点では、最大値が記入される。
次に下段の数は、12から各工程の所要日数を順次差し引き、記入する。
ただし、作業の分岐地点では、最小値が記入される。
上図において、緑色の矢線は、赤枠線内の上段の数と下段の数が一致している地点を結
んだものである。この道順を、クリティカル・パスという。このパス上の作業のどれかを遅ら
せると、全体の日程に影響が出てくるので、クリティカルと呼ばれる所以である。このパス以
外のところは、多少作業が遅れても、全体の工程に影響を与えることはない。
みなさんも、合理的なスケジュールを設計して、限りある時間を有効に使いませんか?
(参考文献:木下栄蔵 著 好奇心の数学(電気書院))