
丂妛廗巜摫梫椞偐傜丄寁嶼広偑徚偊偰媣偟偄丅崱愱栧崅峑偱峴傢傟偰偄傞寁嶼媄弍専掕偼
愄丄寁嶼広専掕偩偭偨偲暦偔丅乮偲偒偳偒擭攝偺曽偑尵偄娫堘偊傞偺偱丄懡暘偦偆偩傠偆丅乯
丂揹戩偺峀斖側晛媦丄婡擻偺崅搙壔丄儕乕僘僫僽儖側抣抜偵傛傝丄傕偼傗寁嶼広偑暅妶偡傞
偙偲偼奆柍偱偁傞丅偟偐偟丄堦帪婜傪夋偟偨寁嶼広傪偙偺傑傑朰傟嫀傞偵偼擡傃側偄丅偦偺懌
愓傪偙偺儂乕儉儁乕僕偵巆偟偰偍偔偙偲偵偟傛偆丅
丂寁嶼広偼丄懳悢偺惈幙偵婎偯偄偰嶌傜傟偰偄傞丅傑偢丄懳悢栚惙偵偮偄偰惍棟偟傛偆丅
丂懳悢娭悢 倷亖倢倧倗 x丂偵偍偄偰丄倶亖侾丄俀丄丒丒丒丄侾侽偵偍偗傞抣乮嬤帡抣乯偼丄師偺昞偺捠傝
偱偁傞丅
| 倶 | 侾 | 俀 | 俁 | 係 | 俆 | 俇 | 俈 | 俉 | 俋 | 侾侽 |
| 倷 | 0.0000 | 0.3010 | 0.4771 | 0.6021 | 0.6990 | 0.7782 | 0.8451 | 0.9031 | 0.9542 | 1.0000 |
丂偙偺 倷 偺抣傪丄尨揰偐傜偺嫍棧偲偟偰丄倢倧倗 x 偺偲偙傠偵丄倶丂偲悢捈慄忋偵栚惙傞丅偙偺傛
偆偵偟偰栚惙偭偨栚惙傪懳悢栚惙偲偄偆丅偙傟偵懳偟偰丄晛捠偺暔嵎偟偺栚惙傪摍暘栚惙偲
偄偆丅
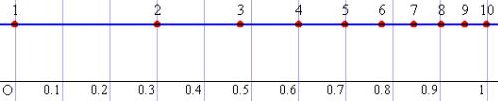
丂懳悢栚惙
丂摍暘栚惙
丂懳悢栚惙偺曽娽巻偼懳悢曽娽巻偲偄傢傟丄怉暔偺惉挿婰榐側偳丄摍暘栚惙偱偼尒偊側偄
摿挜傪柧傜偐偵偡傞偲偒偵梡偄傜傟傞丅
丂寁嶼広偼丄戜広乮奜広乯丄妸広乮撪広乯丄僇乕僜儖乮昗慄乯偺俁偮偺晹暘偐傜側傞丅
戜広忋偵偼丄俙広丄俢広偺俀偮偺懳悢栚惙偑栚惙傜傟偰偄傞丅
丂丂俙広丒丒丒嵍抂偺栚惙偑侾丄塃抂偺栚惙偑侾侽侽 丂乮扨埵偺挿偝偑俠広偺扨埵偺挿偝偺敿暘乯
丂丂俢広丒丒丒嵍抂偺栚惙偑侾丄塃抂偺栚惙偑侾侽
妸広忋偵偼丄俛広丄俠広丄俠俬広乮媡俠広乯偺俁偮偺懳悢栚惙偑栚惙傜傟偰偄傞丅
丂丂俛広丒丒丒嵍抂偺栚惙偑侾丄塃抂偺栚惙偑侾侽侽 丂乮扨埵偺挿偝偑俠広偺扨埵偺挿偝偺敿暘乯
丂丂俠広丒丒丒嵍抂偺栚惙偑侾丄塃抂偺栚惙偑侾侽
丂丂俠俬広丒丒丒嵍抂偺栚惙偑侾侽丄塃抂偺栚惙偑侾丂丂
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮俠広偲扨埵偺挿偝偼摨偠偱丄栚惙偺岦偒偑斀懳乯
埲忋偐傜丄寁嶼広偺奜娤偼師偺傛偆側傕偺偲側傞丅
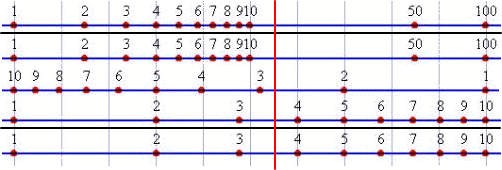 |
俙広 | 戜広偼屌掕 |
| 俛広 | 妸広偼帺桼 偵嵍塃傊摦 偐偣傞 |
|
| 俠俬広 | ||
| 俠広 | ||
| 俢広 | ||
| 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 昗慄乮帺桼偵嵍塃傊堏摦壜乯 | ||
寁嶼広偺娭學
乮侾乯丂俠広偲俢広偺娭學
丂丂丂丂丂俠広偺倎丄倐 偲俢広偺們丄倓偑偦傟偧傟堦抳偡傞偲偒丄倎 丗 倐亖們 丗 倓丂丂乮栚惙偑斾椺乯
乮俀乯丂俠俬広偲俢広偺娭學
丂丂丂丂丂俠俬広偺倎丄倐 偲俢広偺們丄倓偑偦傟偧傟堦抳偡傞偲偒丄倎們亖倐倓丂丂乮栚惙偺愊偑堦掕乯
乮俁乯丂A広偲D広偺娭學
丂丂丂丂丂俙広偺倎偲俢広偺倐偑堦抳偡傞偲偒丄倎偼倐偺暯曽偲側傞丅
乮係乯丂俠広偲俠俬広偺娭學
丂丂丂丂丂俠広偺倎偲俠俬広偺倐偑堦抳偡傞偲偒丄倎倐亖侾侽
丂丂丂亂悢妛揑崻嫆亃
丂丂丂丂丂乮侾乯丂倢倧倗 倐 亅 倢倧倗 a 亖倢倧倗 d 亅 倢倧倗 c 傛傝柧傜偐丅
丂丂丂丂丂乮俀乯丂(侾亅倢倧倗 倐 )亅乮侾亅倢倧倗 a )亖倢倧倗 d 亅 倢倧倗
c 傛傝柧傜偐丅
丂丂丂丂丂乮俁乯丂(侾/俀乯倢倧倗 a 亖倢倧倗 倐 傛傝柧傜偐丅
丂丂丂丂丂乮係乯丂侾亅倢倧倗 倐 亖 倢倧倗 a 傛傝柧傜偐丅
寁嶼広偺寁嶼曽朄
乮侾乯丂忔朄丒丒丒俠俬広偲俢広乮傑偨偼俠広偲俢広乯傪梡偄傞丅
丂丂丂椺丂倎亊倐 偺寁嶼
丂丂丂丂丂丂俢広偺栚惙倎偵俠俬広偺栚惙倐傪堦抳偝偣傞丅偙偺偲偒丄俠俬広偺栚惙侾偵堦抳偡傞
丂丂丂丂丂俢広偺栚惙偺抣偑丄倎亊倐 偺摎偱偁傞丅
丂丂乮捛婰乯丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傛偍偡偗乿偝傫偐傜丄懳悢広偺棙梡椺傪
丂丂丂丂丂丂捀偄偨丅乮暯惉俀俇擭係寧俀俆擔晅偗乯
丂丂丂丂埲壓偺傛偆偵丄懳悢広俠丄俢傪偢傜偟偰廳偹偨偲偒丄栚惙 倎丄倐丄們 (偡傋偰惓偺悢)丂偵
丂丂丂偮偄偰丄丂倎亊倐亖們丂偑惉傝棫偮丅
丂丂丂丂丂丂丂乮幚嵺偺寁嶼広巊梡椺乯
丂丂丂丂丂丂
丂丂乮僐儊儞僩乯丂俠広偺乽侾丂丄俀乿偲俢広偺乽侾丏俆丂丄俁乿偑偦傟偧傟堦抳偡傞偺偱丄
丂丂丂丂丂丂丂丂侾 丗 俀亖侾丏俆 丗 俁丂傛傝丄丂侾丏俆亊俀亖俁丂偑惉傝棫偮丅
丂丂丂丂丂丂丂丂丏丏丏偲偄偆傛傝傕丄乽俀偼丄侾偺俀攞側偺偱丄侾丏俆偺俀攞偼俁乿偲峫偊傞曽偑帺慠
丂丂丂丂丂丂丂丂偐側丠
丂丂丂丂丂丂丂丂丂俠広偲俢広偼摨偠栚惙傝側偺偱丄倢倧倗 們 亅 倢倧倗 倎 亖 倢倧倗 倐 亅 倢倧倗 侾
丂丂丂丂丂丂丂丂偡側傢偪丄丂倢倧倗 侾亖侽丂傛傝丄丂倢倧倗 們 亖 倢倧倗 倎 亄 倢倧倗 倐 亖 倢倧倗 乮倎亊倐乯
丂丂丂丂丂丂丂丂丂傛偭偰丄丂倎亊倐 亖 們丂偑惉傝棫偮丅
乮俀乯丂彍朄丒丒丒俠広偲俢広傪梡偄傞丅
丂丂丂椺丂倎亐倐 偺寁嶼
丂丂丂丂丂丂俢広偺栚惙倎偵俠広偺栚惙倐傪堦抳偝偣傞丅偙偺偲偒丄俠広偺栚惙侾偵堦抳偡傞俢
丂丂丂丂丂広偺栚惙偺抣偑丄倎亐倐 偺摎偱偁傞丅
乮俁乯丂暯曽偲暯曽崻丒丒丒A広偲D広傪梡偄傞丅
丂丂丂寁嶼偺巇曽偼丄寁嶼広偺娭學偐傜柧傜偐偱偁傠偆丅
乮寁嶼椺乯丂侾俀丏俁亊係俆俇 傪寁嶼広偱峴偆応崌
丂丂丂侾俀丏俁亊係俆俇
丂 亖乮侾丏俀俁亊侾侽乯亊乮係丏俆俇亊侾侽侽乯亖乮侾丏俀俁亊係丏俆俇乯亊侾侽侽侽亖俆丏俇侾亊侾侽侽侽亖俆俇侾侽
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂偙偺晹暘偵懳偟偰丄寁嶼広傪巊梡
丂寁嶼広傪梡偄傞偲偒丄岆嵎傪峫椂偟側偗傟偽側傜側偄丅忋偺寁嶼偼丄惓偟偔偼俆俇侽俉丏俉
偱偁傞丅偟偐偟丄揹戩偑側偄帪戙偵偍偄偰丄彫悢偺妡偗嶼丄妱傝嶼側偳傪峴偆偲偒丄寁嶼広
偼杮摉偵偁傝偑偨偐偭偨丅懡暘崱偺揹戩偵懳偡傞巚偄埲忋偩傠偆丅妛峑嫵堢偵偍偄偰寁
嶼広傪妛傫偩嵟屻偺悽戙乮懡暘丠乯偲偟偰丄偙偺巚偄傪惀旕屻悽偵揱偊偰偄偗偨傜偲峫偊
傞師戞偱偁傞丅
乮嶲峫暥專丗杮晹丂嬒丂挊丂悢嘥偺尋媶乮墵暥幮乯
丂丂丂丂丂丂丂 栴栰寬懢榊丂娔廋丂弔擔惓暥丂曇丂岞幃廤乮壢妛怴嫽幮儌僲僌儔僼乯乯
(捛婰乯丂寁嶼広偺婎慴偵側傞懳悢広偼丄侾俇俀侽擭僀僊儕僗偺僈儞僞乕偵傛偭偰敪柧偝傟偨丅
乮捛婰乯丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傛偍偡偗乿偝傫偐傜丄乽暯曽広偲僺僞僑儔僗偺
丂丂丂丂掕棟乿偲戣偟偰丄偛搳峞偄偨偩偄偨丅乮暯惉俀俈擭俇寧俈擔晅偗乯
丂徹柧偼婰偟傑偣傫偑丄偲傝偁偊偢徯夘丅
丂俀偮偺暯曽広A丄B偵偍偄偰丄A偺栚惙倎偲B偺栚惙侽丄A偺栚惙們偲B偺栚惙倐偑偦傟偧傟廳
側傞傛偆偵偍偔偲丄栚惙倎丄倐丄們(倎丄倐丄們偼堎側傞惓偺悢)偺娫偵
丂丂丂丂倎2亄倐2亖們2
偲偄偆娭學幃偑惉傝棫偮丅暯曽広偑庤帩偪偵側偄偺偱丄奺帺偛妋擣偍婅偄偟傑偡丅
乮僐儊儞僩乯丂俛広偵偼乽侽乿偼側偄偼偢側偺偩偑丏丏丏丅寁嶼広偼壛尭嶼偑嬯庤側偺偱丄埫嶼傗
丂丂丂丂丂丂懠偺俠広丄俢広傕妶梡偟側偄偲弌棃側偄傛偆側丏丏丏梊姶丠