ラランの試み　　　　　　　　　　　　　　　　　　　　　　　

　Ｙ＝ａＸⁿ の形の関数は、技術の分野で、よく使われる関数である。
ｎ＝２ のときは、Ｙ＝ａＸ² で放物線を表し、ｎ＝０．５ のときは、 となる。
この関数のグラフを、等分目盛の座標方眼紙に書くと、いろいろな曲線の形が得られる。

　
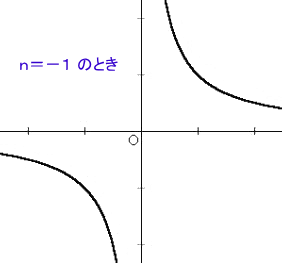
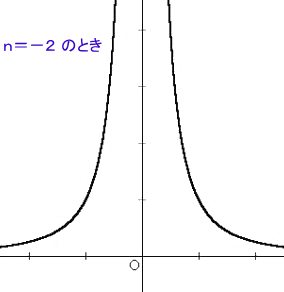
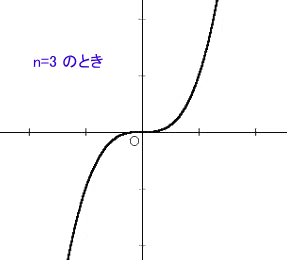
　　（注意）　これらの曲線は、便宜上 ａ＞０
　　　　　　　と仮定した。

　　　このように、単にグラフの概形を書いて、
　　その美しさを堪能するだけならば、それは
　　それで一つの数学である。
　　　しかし、技術の世界では、このグラフを利
　　用して、物事の判断をしなければならない。
　　　そのとき、いくつかの難しい点が出現する。
　　ａ や ｎ の値がいくらか複雑なとき、このよう
　　なグラフを書くことは、非常に困難であるとい
　　うこと、そして、そのグラフで値を読み取る計
　　算の場合、十分な精度を得ることができない
　　ということである。


　１８４３年ラランは、曲線を直線に変換する考えを提出し、このことより、時間の大きな節約
と計算精度の非常な向上をもたらした。
　対数目盛を、Ｘ軸、Ｙ軸に用いる。（原点からの距離 logＸ に新しい目盛Ｘを対応させる。）
このとき、関数 Ｙ＝ａＸⁿ は単に一次関数 Ｙ＝ｎＸ＋ａ に変換される。

例　関数

は、一次関数 Ｙ＝(1/4)Ｘ に変換される。両者のグラフは次のようになる。

　

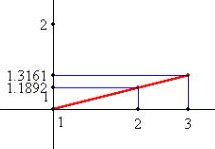
　　　グラフが簡単にパソコンで描け
　　る現代にあっては、ラランの試み
　　は時代遅れという批判を受ける
　　かもしれない。


しかし、グラフを使って、精密に計算をやろうという彼の試みは、現代に生きる我々が忘れ
てしまった大切なものを思い出させてくれる。何でも楽をしようとする我々に対する警鐘で
もある。

（参考文献：コロソフ著　木村君男　訳　数学課外よみもの（東京図書））