
当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(令和4年10月1日付け)
A+B+C=π、nを整数とするとき、次の等式を証明せよ。
(1)
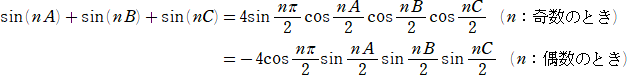
(2)
(追記) よおすけさんから追記いただきました。(令和6年12月1日付け)
(3) 次の値を求めよ。
(tanA+tanB)/tanC−tanA・tanB
(答)(1) nが奇数のとき、
sin(nA)+sin(nB)+sin(nC)
=2sin((nA+nB)/2)cos((nA−nB)/2)+2sin((nA+nB)/2)cos((nA+nB)/2)
=2sin((nA+nB)/2)(cos((nA−nB)/2)+cos((nA+nB)/2))
=2sin((nA+nB)/2)・2cos(nA/2)cos(nB/2)
=4sin(nπ/2)cos(nA/2)cos(nB/2)cos(nC/2)
nが偶数のとき、
sin(nA)+sin(nB)+sin(nC)
=2sin((nA+nB)/2)cos((nA−nB)/2)−2sin((nA+nB)/2)cos((nA+nB)/2)
=2sin((nA+nB)/2)(cos((nA−nB)/2)−cos((nA+nB)/2))
=2sin((nA+nB)/2)・2sin(nA/2)sin(nB/2)
=−4cos(nπ/2)sin(nA/2)sin(nB/2)sin(nC/2)
(2) A+B+C=π より、 nA+nB+nC=nπ すなわち、 nA+nB=nπ−nC
このとき、 tan(nA+nB)=tan(nπ−nC)=−tan(nC) なので、
(tan(nA)+tan(nB))/(1−tan(nA)tan(nB))=−tan(nC)
よって、
tan(nA)+tan(nB)
=−tan(nC)(1−tan(nA)tan(nB))=−tan(nC)+tan(nA)tan(nB)tan(nC)
より、
(コメント) △ABCにおいて、 tan(A)+tan(B)+tan(C)=tan(A)tan(B)tan(C) が
成り立ちますが、これは私の推しの(お気に入りの)等式です!
(→ 参考)
(3) (tanA+tanB)/tanC−tanA・tanB
=(tanA+tanB−tanA・tanB・tanC)/tanC
=(−tanC)/tanC
=−1
以下、工事中!