同じ大きさ、同じ向きの２枚の三角形がある。１つの三角形の上に、もう一方の三角形を
任意に重ねる。ただし、各辺は互いに２点で交わるものとする。
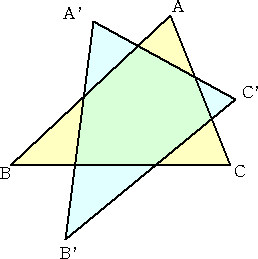
このとき、この三角形上の１点に針を刺して、その点の周りに２枚の三角形を回転させる
と、ぴったり重なるという。このような点を求めよ。
（答） 次のような点が求めるものである。
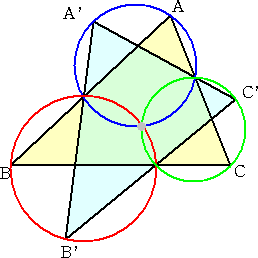
なぜ、上図のような作図が可能なのか、解析してみよう。
いま、回転の中心 Ｏ が求まったものとする。
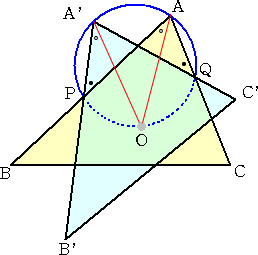左図において、∠Ａ＝∠Ａ’ より、４点 Ａ、Ａ’、Ｐ、Ｑ を通る円が存在する。また、
∠ＯＡＰ＝∠ＯＡ’Ｐ
であるので、∠ＡＯＡ’＝∠ＡＰＡ’ が成り立つ。
したがって、円周角の定理により、
点 Ｏ は、４点 Ａ、Ａ’、Ｐ、Ｑ を通る円周上に
存在する。
以上から、３つの円の交点として求める点が得
られることが分かる。
この問題に関して、当ＨＰがいつもお世話になっているＨＮ「ＦＮ」さんからのコメントです。
（平成２２年１２月１０日付け）
普通に考えれば、線分ＡＡ’の垂直２等分線と線分ＢＢ’の垂直２等分線の交点でいいと思
います。（仰るとおりです。ただ、３つの円の交点という物言いに引かれました！）
この問題には３つの仮定があります。
(1) ２つの三角形は合同で向きが同じ
(2) ２つの三角形の各辺は互いに２点で交わる
(3) ある点を中心にした回転により一方が他方に移る
このとき回転の中心を求めなさいという問題です。
パズルで証明を要求するわけにはいかないので(3)は必要で、三角形の内部に回転の中
心があるために(2)がつけてあるのでしょう。パズルとしてはこれでいいですが、数学として
は仮定が多すぎるように思います。
条件(1)が必要なのは明らかですが、(2)(3)は多分不要です。もちろん(1)の他に多少の条
件は必要です。また回転の中心が三角形の内部にあることは要請しないとします。次の形
で成立すると思います。
平面上の２つの三角形ＡＢＣとＡ’Ｂ’Ｃ’が同じ向きに合同で、ＡＢとＡ’Ｂ’は平行で
ないとする。
このとき点Ｐが存在して、点Ｐのまわりの回転によって△ＡＢＣは△Ａ’Ｂ’Ｃ’に移る
ことを示せ。
（注） 「ＡＢとＡ’Ｂ’は平行でないとする」は必要です。ＡＢとＡ’Ｂ’が平行であれば平行移
動で移るので回転では移りません。だから、同じ向きに合同な２つの三角形は平行移
動または回転によって移すことができるという形でもかまいません。
（コメント） ＦＮさん、ありがとうございます。２つの合同な三角形を平面上に「ポン！」と適当
に置いた場合に、１つを手にとって重ねるのではなく、回転によって重ねたいという
ことで、解答を書きやすい形の条件をいくつか追加して問題としました。この問題の
原典は、次の問題です。
平面上に長さの等しい２つの線分ＡＢ、Ａ’Ｂ’がある。平面上のある点Ｏの周りに回
転させると互いに重なるという。この点Ｏを作図せよ。
線分が逆向きに平行の場合は、そのような点を作図することは可能（平行四辺形の対角
線の交点）ですが、同じ向きに平行の場合は不可能ですね！
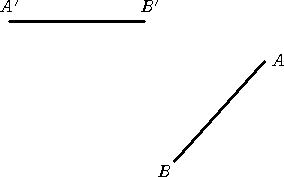
ＦＮさんが仰っているように、対応する２点間を結ぶ線分の垂直２等分線を作図し、その交
点を求めればよい。
「対応する２点間を結ぶ線分の垂直２等分線を作図し、その交点を求める」ことが、この問
題の解法の定石ですが、対応する２点間を結ぶ線分の垂直２等分線を作図するかわりに、
円を作図することにしたのが、本題の解答です。
円を作図するには、「２つの弦の垂直２等分線の交点の作図」が必須ですが、私が使って
いる描画ソフトでは、３点を指定するだけで円を描いてくれます。この機能に誘惑されたのか
もしれません．．．ｆ(^_^;) 。
（追記） 平成２３年２月５日付け
上記の問題は、合同な三角形を２枚用いるが、その三角形の書かれた正方形とそのコピ
ーを用いると、「正方形を重ねる」と同種の問題となる。このことを、当ＨＰがいつもお世話に
なっているＨＮ「攻略法」さんが指摘された。
本来は、三角形が描かれた２枚の透明な用紙を用意することですが、ＯＨＰ用紙のような
透明な用紙に、三角形ＡＢＣを写し取る。それを、コピー機で複製する。
（同じ大きさの用紙に、向きと位置が同じになるように写し取ればよい）
２枚の用紙を、三角形ABC、三角形A’B’C’に重なるように配置し、用紙の対辺の交点を
Ｕ、Ｄ、Ｌ、Ｒとすると、線分ＵＤ、ＬＲの交点が求める回転の中心となる。
（コメント） 攻略法さん、ありがとうございます。正方形が重なれば、当然、三角形も重なり
ますね！