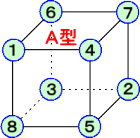
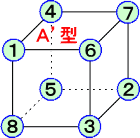
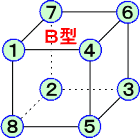
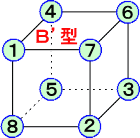
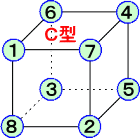
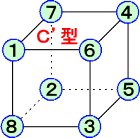
| A |
B |
C |
D |
E |
F |
G |
H |
型 |
| 1 |
4 |
6 |
7 |
8 |
5 |
3 |
2 |
A’ |
| 1 |
4 |
7 |
6 |
8 |
5 |
2 |
3 |
B’ |
| 1 |
4 |
8 |
5 |
7 |
6 |
2 |
3 |
B |
| 1 |
4 |
8 |
5 |
6 |
7 |
3 |
2 |
A |
| 1 |
6 |
4 |
7 |
8 |
3 |
5 |
2 |
A |
| 1 |
6 |
7 |
4 |
8 |
3 |
2 |
5 |
C |
| 1 |
6 |
8 |
3 |
7 |
4 |
2 |
5 |
C’ |
| 1 |
6 |
8 |
3 |
4 |
7 |
5 |
2 |
A’ |
| 1 |
7 |
4 |
6 |
8 |
2 |
5 |
3 |
B |
| 1 |
7 |
6 |
4 |
8 |
2 |
3 |
5 |
C’ |
| 1 |
7 |
8 |
2 |
6 |
4 |
3 |
5 |
C |
| 1 |
7 |
8 |
2 |
4 |
6 |
5 |
3 |
B’ |
| 1 |
8 |
4 |
5 |
7 |
2 |
6 |
3 |
B’ |
| 1 |
8 |
4 |
5 |
6 |
3 |
7 |
2 |
A’ |
| 1 |
8 |
6 |
3 |
7 |
2 |
4 |
5 |
C |
| 1 |
8 |
6 |
3 |
4 |
5 |
7 |
2 |
A |
| 1 |
8 |
7 |
2 |
6 |
3 |
4 |
5 |
C’ |
| 1 |
8 |
7 |
2 |
4 |
5 |
6 |
3 |
B |
| 2 |
3 |
5 |
8 |
7 |
6 |
4 |
1 |
A |
| 2 |
3 |
7 |
6 |
8 |
5 |
1 |
4 |
B |
| 2 |
3 |
7 |
6 |
5 |
8 |
4 |
1 |
A’ |
| 2 |
3 |
8 |
5 |
7 |
6 |
1 |
4 |
B’ |
| 2 |
5 |
3 |
8 |
7 |
4 |
6 |
1 |
A’ |
| 2 |
5 |
7 |
4 |
8 |
3 |
1 |
6 |
C’ |
| 2 |
5 |
7 |
4 |
3 |
8 |
6 |
1 |
A |
| 2 |
5 |
8 |
3 |
7 |
4 |
1 |
6 |
C |
| 2 |
7 |
3 |
6 |
8 |
1 |
5 |
4 |
B’ |
| 2 |
7 |
3 |
6 |
5 |
4 |
8 |
1 |
A |
| 2 |
7 |
5 |
4 |
8 |
1 |
3 |
6 |
C |
| 2 |
7 |
5 |
4 |
3 |
6 |
8 |
1 |
A’ |
| 2 |
7 |
8 |
1 |
5 |
4 |
3 |
6 |
C’ |
| 2 |
7 |
8 |
1 |
3 |
6 |
5 |
4 |
B |
| 2 |
8 |
3 |
5 |
7 |
1 |
6 |
4 |
B |
| 2 |
8 |
5 |
3 |
7 |
1 |
4 |
6 |
C’ |
| 2 |
8 |
7 |
1 |
5 |
3 |
4 |
6 |
C |
| 2 |
8 |
7 |
1 |
3 |
5 |
6 |
4 |
B’ |
| 3 |
2 |
5 |
8 |
6 |
7 |
4 |
1 |
B |
| 3 |
2 |
6 |
7 |
8 |
5 |
1 |
4 |
A |
| 3 |
2 |
6 |
7 |
5 |
8 |
4 |
1 |
B’ |
| 3 |
2 |
8 |
5 |
6 |
7 |
1 |
4 |
A’ |
| 3 |
5 |
2 |
8 |
6 |
4 |
7 |
1 |
B’ |
| 3 |
5 |
6 |
4 |
8 |
2 |
1 |
7 |
C |
| 3 |
5 |
6 |
4 |
2 |
8 |
7 |
1 |
B |
| 3 |
5 |
8 |
2 |
6 |
4 |
1 |
7 |
C’ |
| 3 |
6 |
2 |
7 |
8 |
1 |
5 |
4 |
A’ |
| 3 |
6 |
2 |
7 |
5 |
4 |
8 |
1 |
B |
| 3 |
6 |
5 |
4 |
8 |
1 |
2 |
7 |
C’ |
| 3 |
6 |
5 |
4 |
2 |
7 |
8 |
1 |
B’ |
|
|
| A |
B |
C |
D |
E |
F |
G |
H |
型 |
| 3 |
6 |
8 |
1 |
5 |
4 |
2 |
7 |
C |
| 3 |
6 |
8 |
1 |
2 |
7 |
5 |
4 |
A |
| 3 |
8 |
2 |
5 |
6 |
1 |
7 |
4 |
A |
| 3 |
8 |
5 |
2 |
6 |
1 |
4 |
7 |
C |
| 3 |
8 |
6 |
1 |
5 |
2 |
4 |
7 |
C’ |
| 3 |
8 |
6 |
1 |
2 |
5 |
7 |
4 |
A’ |
| 4 |
1 |
5 |
8 |
7 |
6 |
2 |
3 |
A’ |
| 4 |
1 |
5 |
8 |
6 |
7 |
3 |
2 |
B’ |
| 4 |
1 |
6 |
7 |
5 |
8 |
3 |
2 |
B |
| 4 |
1 |
7 |
6 |
5 |
8 |
2 |
3 |
A |
| 4 |
5 |
1 |
8 |
7 |
2 |
6 |
3 |
A |
| 4 |
5 |
1 |
8 |
6 |
3 |
7 |
2 |
B |
| 4 |
5 |
6 |
3 |
7 |
2 |
1 |
8 |
C’ |
| 4 |
5 |
6 |
3 |
1 |
8 |
7 |
2 |
B’ |
| 4 |
5 |
7 |
2 |
6 |
3 |
1 |
8 |
C |
| 4 |
5 |
7 |
2 |
1 |
8 |
6 |
3 |
A’ |
| 4 |
6 |
1 |
7 |
5 |
3 |
8 |
2 |
B’ |
| 4 |
6 |
5 |
3 |
7 |
1 |
2 |
8 |
C |
| 4 |
6 |
5 |
3 |
1 |
7 |
8 |
2 |
B |
| 4 |
6 |
7 |
1 |
5 |
3 |
2 |
8 |
C’ |
| 4 |
7 |
1 |
6 |
5 |
2 |
8 |
3 |
A’ |
| 4 |
7 |
5 |
2 |
6 |
1 |
3 |
8 |
C’ |
| 4 |
7 |
5 |
2 |
1 |
6 |
8 |
3 |
A |
| 4 |
7 |
6 |
1 |
5 |
2 |
3 |
8 |
C |
| 5 |
2 |
3 |
8 |
4 |
7 |
6 |
1 |
C’ |
| 5 |
2 |
4 |
7 |
8 |
3 |
1 |
6 |
A’ |
| 5 |
2 |
4 |
7 |
3 |
8 |
6 |
1 |
C |
| 5 |
2 |
8 |
3 |
4 |
7 |
1 |
6 |
A |
| 5 |
3 |
2 |
8 |
4 |
6 |
7 |
1 |
C |
| 5 |
3 |
4 |
6 |
8 |
2 |
1 |
7 |
B’ |
| 5 |
3 |
4 |
6 |
2 |
8 |
7 |
1 |
C’ |
| 5 |
3 |
8 |
2 |
4 |
6 |
1 |
7 |
B |
| 5 |
4 |
2 |
7 |
8 |
1 |
3 |
6 |
A |
| 5 |
4 |
2 |
7 |
3 |
6 |
8 |
1 |
C’ |
| 5 |
4 |
3 |
6 |
8 |
1 |
2 |
7 |
B |
| 5 |
4 |
3 |
6 |
2 |
7 |
8 |
1 |
C |
| 5 |
4 |
8 |
1 |
3 |
6 |
2 |
7 |
B’ |
| 5 |
4 |
8 |
1 |
2 |
7 |
3 |
6 |
A’ |
| 5 |
8 |
2 |
3 |
4 |
1 |
7 |
6 |
A’ |
| 5 |
8 |
3 |
2 |
4 |
1 |
6 |
7 |
B’ |
| 5 |
8 |
4 |
1 |
3 |
2 |
6 |
7 |
B |
| 5 |
8 |
4 |
1 |
2 |
3 |
7 |
6 |
A |
| 6 |
1 |
3 |
8 |
7 |
4 |
2 |
5 |
A |
| 6 |
1 |
3 |
8 |
4 |
7 |
5 |
2 |
C |
| 6 |
1 |
4 |
7 |
3 |
8 |
5 |
2 |
C’ |
| 6 |
1 |
7 |
4 |
3 |
8 |
2 |
5 |
A’ |
| 6 |
3 |
1 |
8 |
7 |
2 |
4 |
5 |
A’ |
| 6 |
3 |
1 |
8 |
4 |
5 |
7 |
2 |
C’ |
|
|
| A |
B |
C |
D |
E |
F |
G |
H |
型 |
| 6 |
3 |
4 |
5 |
7 |
2 |
1 |
8 |
B |
| 6 |
3 |
4 |
5 |
1 |
8 |
7 |
2 |
C |
| 6 |
3 |
7 |
2 |
4 |
5 |
1 |
8 |
B’ |
| 6 |
3 |
7 |
2 |
1 |
8 |
4 |
5 |
A |
| 6 |
4 |
1 |
7 |
3 |
5 |
8 |
2 |
C |
| 6 |
4 |
3 |
5 |
7 |
1 |
2 |
8 |
B’ |
| 6 |
4 |
3 |
5 |
1 |
7 |
8 |
2 |
C’ |
| 6 |
4 |
7 |
1 |
3 |
5 |
2 |
8 |
B |
| 6 |
7 |
1 |
4 |
3 |
2 |
8 |
5 |
A |
| 6 |
7 |
3 |
2 |
4 |
1 |
5 |
8 |
B |
| 6 |
7 |
3 |
2 |
1 |
4 |
8 |
5 |
A’ |
| 6 |
7 |
4 |
1 |
3 |
2 |
5 |
8 |
B’ |
| 7 |
1 |
2 |
8 |
6 |
4 |
3 |
5 |
B |
| 7 |
1 |
2 |
8 |
4 |
6 |
5 |
3 |
C’ |
| 7 |
1 |
4 |
6 |
2 |
8 |
5 |
3 |
C |
| 7 |
1 |
6 |
4 |
2 |
8 |
3 |
5 |
B’ |
| 7 |
2 |
1 |
8 |
6 |
3 |
4 |
5 |
B’ |
| 7 |
2 |
1 |
8 |
4 |
5 |
6 |
3 |
C |
| 7 |
2 |
4 |
5 |
6 |
3 |
1 |
8 |
A |
| 7 |
2 |
4 |
5 |
1 |
8 |
6 |
3 |
C’ |
| 7 |
2 |
6 |
3 |
4 |
5 |
1 |
8 |
A’ |
| 7 |
2 |
6 |
3 |
1 |
8 |
4 |
5 |
B |
| 7 |
4 |
1 |
6 |
2 |
5 |
8 |
3 |
C’ |
| 7 |
4 |
2 |
5 |
6 |
1 |
3 |
8 |
A’ |
| 7 |
4 |
2 |
5 |
1 |
6 |
8 |
3 |
C |
| 7 |
4 |
6 |
1 |
2 |
5 |
3 |
8 |
A |
| 7 |
6 |
1 |
4 |
2 |
3 |
8 |
5 |
B |
| 7 |
6 |
2 |
3 |
4 |
1 |
5 |
8 |
A |
| 7 |
6 |
2 |
3 |
1 |
4 |
8 |
5 |
B’ |
| 7 |
6 |
4 |
1 |
2 |
3 |
5 |
8 |
A’ |
| 8 |
1 |
2 |
7 |
5 |
4 |
3 |
6 |
B’ |
| 8 |
1 |
2 |
7 |
3 |
6 |
5 |
4 |
C |
| 8 |
1 |
3 |
6 |
5 |
4 |
2 |
7 |
A’ |
| 8 |
1 |
3 |
6 |
2 |
7 |
5 |
4 |
C’ |
| 8 |
1 |
5 |
4 |
3 |
6 |
2 |
7 |
A |
| 8 |
1 |
5 |
4 |
2 |
7 |
3 |
6 |
B |
| 8 |
2 |
1 |
7 |
5 |
3 |
4 |
6 |
B |
| 8 |
2 |
1 |
7 |
3 |
5 |
6 |
4 |
C’ |
| 8 |
2 |
3 |
5 |
1 |
7 |
6 |
4 |
C |
| 8 |
2 |
5 |
3 |
1 |
7 |
4 |
6 |
B’ |
| 8 |
3 |
1 |
6 |
5 |
2 |
4 |
7 |
A |
| 8 |
3 |
1 |
6 |
2 |
5 |
7 |
4 |
C |
| 8 |
3 |
2 |
5 |
1 |
6 |
7 |
4 |
C’ |
| 8 |
3 |
5 |
2 |
1 |
6 |
4 |
7 |
A’ |
| 8 |
5 |
1 |
4 |
3 |
2 |
6 |
7 |
A’ |
| 8 |
5 |
1 |
4 |
2 |
3 |
7 |
6 |
B’ |
| 8 |
5 |
2 |
3 |
1 |
4 |
7 |
6 |
B |
| 8 |
5 |
3 |
2 |
1 |
4 |
6 |
7 |
A |
|

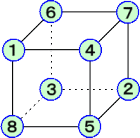
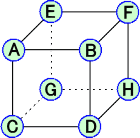 但し、回転して重なる場合も含む。
但し、回転して重なる場合も含む。