下図のように、１４個の○を含む図形がある。○には、１〜１４の数字が、１つずつ入るも
のとする。ただし、一直線上の４つの○の数字の和は、一定とする。どのように入れたらい
いだろうか？
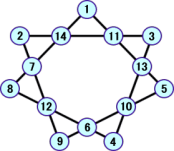
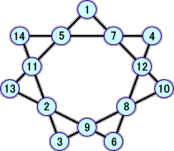
（答） １つの答として、右下図のような場合が考えられる。ただ、答が１つだけという確信が
もてない。別な場合を発見された方、こちらまでメール下さい。
（参考文献：篠原正典 著 逆転の発想で ＩＴ を有効活用する
― Cambridge University Millennium Mathematics project より―
（啓林 高数編 Ｎｏ．３２６） （啓林館））
（追記） 題意より、１４個の数は、それぞれ２本の直線上にあるので、各直線上の４つの数
の和は、３０に等しい。実際に、
（１＋２＋３＋・・・＋１３＋１４）×２÷７＝１４×１５÷７＝３０
上の解以外の解を見つけようとして、次のように考えた。
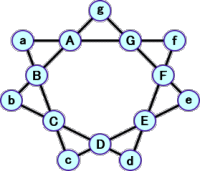左図より、 Ａ＋Ｂ＝３０−ｂ−ｇＢ＋Ｃ＝３０−ａ−ｃ
Ｃ＋Ｄ＝３０−ｂ−ｄ
Ｄ＋Ｅ＝３０−ｃ−ｅ
Ｅ＋Ｆ＝３０−ｄ−ｆ
Ｆ＋Ｇ＝３０−ｅ−ｇ
Ｇ＋Ａ＝３０−ａ−ｆ
という連立方程式において、未知数の個数が１４で、式
の本数が７なので、この連立方程式の自由度は７である。
このとき、ａ、ｂ、ｃ、ｄ、ｅ、ｆ、ｇ を、１から１４までの任意の数として、
残りの未知数は、
Ａ＝１５−ｂ＋ｃ−ｄ＋ｅ−ｆ
Ｂ＝１５−ｃ＋ｄ−ｅ＋ｆ−ｇ
Ｃ＝１５−ａ−ｄ＋ｅ−ｆ＋ｇ
Ｄ＝１５＋ａ−ｂ−ｅ＋ｆ−ｇ
Ｅ＝１５−ａ＋ｂ−ｃ−ｆ＋ｇ
Ｆ＝１５＋ａ−ｂ＋ｃ−ｄ−ｇ
Ｇ＝１５−ａ＋ｂ−ｃ＋ｄ−ｅ
と表される。
上の解は、ａ＝２、ｂ＝８、ｃ＝９、ｄ＝４、ｅ＝５、ｆ＝３、ｇ＝１ の場合で、このとき、
Ａ＝１４、Ｂ＝７、Ｃ＝１２、Ｄ＝６、Ｅ＝１０、Ｆ＝１３、Ｇ＝１１
である。
したがって、ａ、ｂ、ｃ、ｄ、ｅ、ｆ、ｇ の値を、１から１４まで任意に変化させて、
Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇ の値を求め、そのうち、１４個の文字
ａ、ｂ、ｃ、ｄ、ｅ、ｆ、ｇ、Ａ、Ｂ、Ｃ、Ｄ、Ｅ、Ｆ、Ｇ
が全て異なる場合を探せば、上とは別な解が見つかりそうである。
徒然なるままに解を探したところ、次のような解が見つかった。やはり、解は、１通りでは
なかった。
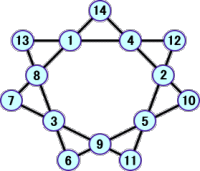
この解は、上の解とは、ある意味で反転になっている。
上で述べた解の探求プログラムによって、確かに、
解は「見つかりそう・・・」なのであるが、大変な計算
が予想され、ちょっと計算の実行をためらっている
ところである。
実際に実行された方、メール下さい。
（再追記） その後、塾生たちの努力により、次の新しい解が発見されたので、報告したい。
左側は、塾生によるもの、右側は、その反転である。
塾生 Ｔ．Ｋ．君による解
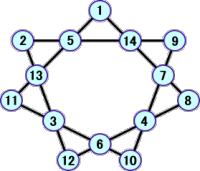
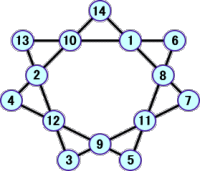
塾生 Ｙ．Ｈ．君による解
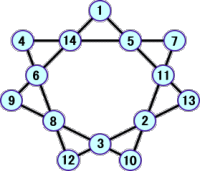
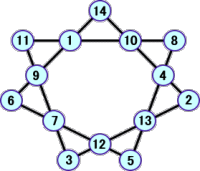
以上で、６個が発見された。もっと解がありそうだ！！
（再々追記）
２００３年７月２２日付けで、 「猫目石」さんという方から変形魔方陣についての情報をいた
だいた。（当ＨＰ掲示板）
七芒星の変形魔方陣の解を、コンピューターで虱潰してみた結果、144個の解が見つかりました。(左右反転解
や各セルを15から引いた解を除いていないので、オリジナルな解は多分36個です)
ちなみに、五芒星では解が存在せず、六芒星では160個の解が存在することも分かりました。
「猫目石」さんに感謝いたします。
（再々々追記） 大森清美 著 魔方陣 （冨山房）によれば、六芒星（６星陣）は、８０個の
解を持ち、七芒星（７星陣）は、７２個の解を持つとのことである。
上記６個の解に加えて、次の解が新しく追加された。分かっている解は、全部で、１０個と
なった！
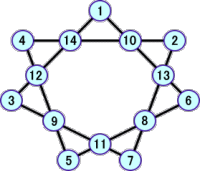
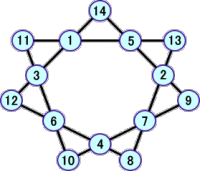
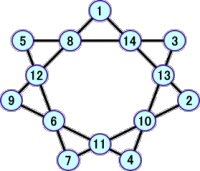
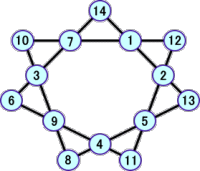
ホームページにて、自らの「魔方陣の研究」についての成果を公開している方がいらっしゃ
ることを、数理パズル入門の未菜実さんに教わりました！
論文集：『魔方陣の研究』 摂田 寛二
ありとあらゆる魔方陣が研究されていて、読むものを圧倒します。是非、皆さんも、お立ち
寄り下さい。
（再々々々追記）
（追記）で述べた解の探求プログラムについて、表計算ソフトＥｘｃｅｌのＶＢＡを利用して考えて
みた。興味ある方は、下記をコピーして試してみてください。ただ、下記のプログラムは未完成
で、まだ無駄な計算を含むものである。ａ、ｂ の値を一つずつ決めて、残りの変数全てを繰り返
すのに、何と（？）、３時間半ぐらいかかるようだ！もうしばらく、検討が必要です．．．。
Sub 変形魔方陣()
Dim a, b, c, d, e, f, g, h As Integer
Range("a2").Select
For a = 1 To 14
For b = 1 To 14
For c = 1 To 14
For d = 1 To 14
For e = 1 To 14
For f = 1 To 14
For g = 1 To 14
With ActiveCell
.Value = 15 - b + c - d + e - f
.Offset(0, 1).Value = 15 - c + d - e + f - g
.Offset(0, 2).Value = 15 - a - d + e - f + g
.Offset(0, 3).Value = 15 + a - b - e + f - g
.Offset(0, 4).Value = 15 - a + b - c - f + g
.Offset(0, 5).Value = 15 + a - b + c - d - g
.Offset(0, 6).Value = 15 - a + b - c + d - e
.Offset(0, 10).Value = a
.Offset(0, 11).Value = b
.Offset(0, 12).Value = c
.Offset(0, 13).Value = d
.Offset(0, 14).Value = e
.Offset(0, 15).Value = f
.Offset(0, 16).Value = g
.Offset(0, 7).Value = "=MAX(RC[-7]:RC[-1],RC[+3]:RC[+9])"
.Offset(0, 8).Value = "=Min(RC[-8]:RC[-2],RC[+2]:RC[+8])"
.Offset(0, 9).Value = "=SUM(RC[-9]:RC[-3],RC[+1]:RC[+7])"
h = (15 - b + c - d + e - f) ^ 2 + (15 - c + d - e + f - g) ^ 2 + (15 - a - d + e - f + g) ^ 2 _
+ (15 + a - b - e + f - g) ^ 2 + (15 - a + b - c - f + g) ^ 2 + (15 + a - b + c - d - g) ^ 2 _
+ (15 - a + b - c + d - e) ^ 2 + a ^ 2 + b ^ 2 + c ^ 2 + d ^ 2 + e ^ 2 + f ^ 2 + g ^ 2
If .Offset(0, 7).Value = 14 And .Offset(0, 8).Value = 1 And .Offset(0, 9).Value = 105 And h = 1015 Then
.Offset(1, 0).Select
Else
.Offset(0, 0).Select
End If
End With
Next g, f, e, d, c, b, a
End Sub
もっと、こうした方がいいよ！というアイデアをお持ちの方、こちらまでメールをお願いします。
（再々々々々追記） 上のプログラムを、ａ＝１、ｂ＝２ の場合について実行してみた。
出力の結果は次の通りである。（解のみ抜粋！！）
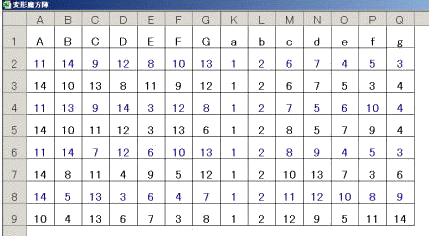
上の表から、次のような新しい解が、１２個発見された。
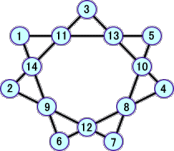
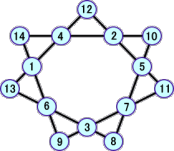
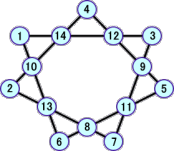
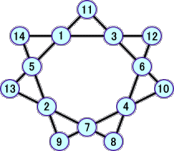
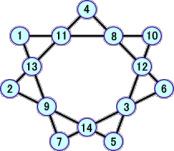
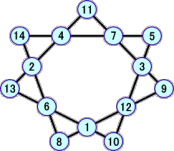
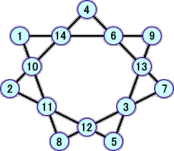
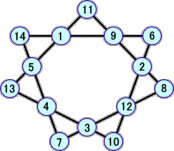
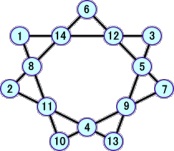
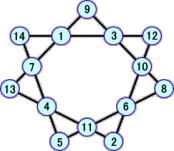
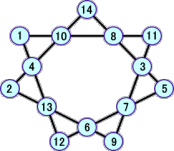
以上から、分かっている解は、全部で、２２個となった！
（顛末記） 表計算ソフトＥｘｃｅｌのＶＢＡを利用して解を求めるために、解の探求プログラムに
従って、上記のようにマクロを組んでみましたが、あまりの遅さに閉口でした。それ
でも、プログラムを多少修正して、ａ＝１ を固定して、ｂ〜ｇ の値を ２〜１４ まで変
化させるのに、試算で３６時間程度でできる目途がたったので、早速日曜日の早
朝から、月曜日の深夜まで我が家のデスクトップパソコンをぶっ続けで稼動させま
した。 ａ の値を ２〜１４まで変化させる必要もありますが、ちょっと挫折しました。
知り合いの電子制御が専門の方に伺うと、「ｆｏｒ〜ｎｅｘｔ文」を７個も使うのは無謀
だとのことでした。アルゴリズムそのものを変えた方がよいとも言われました。
確かにその通りですね！もう少し、プログラムを工夫しないと、パソコンのよさが
発揮できないですね。今後の研究としたいと思います。
この問題に、猫目石さんが取り組まれて、わずか「４．４５３秒」で「解は、７２通り」
という結果を出されました。「スゴイ！！」の一語に尽きます。
私の方は、３６時間パソコンに鞭打って頑張らせたのですが、解は「５８通り」しか
得ることができませんでした。残りの１４通りは、ａ の値が １ 以外の場合です。
参考までに、こちらのページに計算結果をまとめておきます。猫目石さんの解か
らの補充もあわせて、計７２通りの解を提示したいと思います。