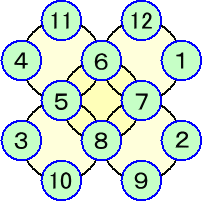
次の空所には数字の 1 、2 、・・・、10、11、12 の何れかがそれぞれ一つずつ入り、
かつ、それぞれの円周上の4つの数字の和は一定になるようにしたい。
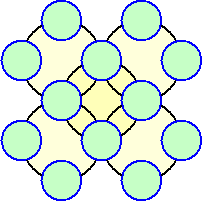
どのように数字を書き入れたらよいであろうか?
(答) 例えば、
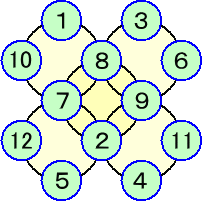
他にも解はあるのかな?適当にやっていたら直ぐ見つかったので、解はたくさんありそう。
らすかるさんが考察されました。解は425通りあるとのこと。らすかるさんに感謝します。
(平成25年9月16日付け)
解が多そうな気がしたのでプログラムで調べました。
{1+2+3+4+Σ(1〜12)}÷4=22 、{9+10+11+12+Σ(1〜12)}÷4=30 から、和が 22〜30 の範
囲であることはすぐにわかります。
また、「和が一定(3)」と同様、和がnになる解と和が 52-n になる解は同数になります。
裏返し、回転、外側の2個の入れ替えを同一視して、和ごとの解は
和が22、和が30 : 15通りずつ 和が23、和が29 : 11通りずつ
和が24、和が28 : 48通りずつ 和が25、和が27:41通りずつ
和が26 : 195通り 全部で、 (15+11+48+41)×2+195=425通り
(コメント) らすかるさんによれば、次が一番綺麗そうだとのこと。確かに数字が順番に並ん
でいて、私の解とは比較にならないくらいの美しさです...!