
2項定理の応用として、「パスカルの三角形」が有名である。最近、「反パスカル的三角形」
というものの存在を知った。
これは、最下段の行以外の数は、すぐ真下の両隣のふたつの数の差の絶対値で定まるよ
うに、正三角形状に数を並べたものである。
例 2行の場合・・・ 1、2、3で作られる正三角形の配列
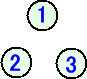
(作り方) 3−2=1 から、上記の1通りが存在。
3行の場合・・・ 1、2、3、4、5、6で作られる正三角形の配列
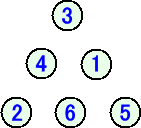
(作り方) 6個から2個選ぶ場合の数は、6C2=15(通り) で、この15通りについて計算式
を列挙すると、
3−2=1、
4−3=1、5−3=2、
5−4=1、6−4=2、
6−5=1 この15組の計算式で、同じ数字を用いているのは不可なので、取消
この中で、4−1=3、6−2=4、6−5=1 を用いた例が上記である。
3−1=2 を用いると不具合が起きて不可能である。
幾つか試行錯誤して、次の例が存在するので、上記の解は唯一解ではないことが分かる。
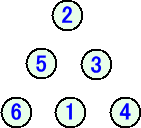
4行の場合・・・ 1、2、3、4、5、6、7、8、9、10で作られる正三角形の配列
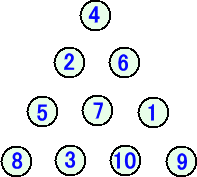
さて、問題です。5行の場合、1、2、3、・・・、14、15で作られる反パスカル的三角形を構
成してください。
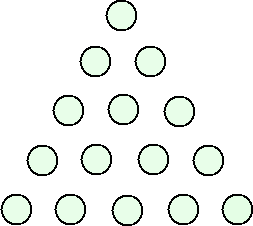
(答) 次のような配列で、左右対称を除けば、解は1通りしかない。

行数が増えてくると、構成するのがだんだんと難しくなる。一体、何行まで、反パスカル的三
角形は存在するだろうか?興味ある読者の方の研究をお待ちしております。
(国際数学オリンピック(2018)で出題された問題では、2018行の反パスカル的三角形は
存在しないらしい。)
(追記) 数学好きの学生さんからご投稿いただきました。(令和5年9月21日付け
反パスカル的三角形は全く知らなかったので、興味深いです。
質問なのですが、5行の場合の反パスカル的三角形はどのように探したのでしょうか?
左右対称を除いて1通りしかないということなので、コンピュータで全探索したのでしょうか?
気になったので質問させていただきました。お時間があるときに返信して頂けると幸いです。
(コメント) 5年前の記事なので、記憶が定かではありませんが、数学オリンピックの問題に
啓発されて、多分、手計算で求めたと思います。
若干、前のページを見直して、作り方を追記しました。3行の場合の(作り方)から分かる
ように、絶対「使えない式」が存在するので、虱潰しで調べたと思います。
以下、工事中!