
�@���}�̂悤�Ȏl�p�`�`�a�b�c������B
�@�@�@�@�@�@
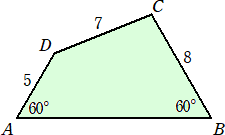
�@���̂Ƃ��A�����`�a�̒��������߂�B
�i���j�@���̐}�������u�ԂɁA���}�̂悤�ɕ⏕���������āA���O�p�`�`�a�d�����̂�
�@�@�@����낤�B
�@�@�@�@�@�@
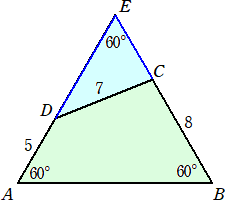
�@���̂Ƃ��A�`�a�����@�Ƃ����A�@�d�c�����|�T�@�A�d�b�����|�W�@�Ȃ̂ŁA�]���藝���A
�@�@�V2���i���|�T�j2�{�i���|�W�j2�|�Q�E�i���|�T�j�i���|�W�j�������U�O��
�@����āA�@��2�|�P�R�����O�@�������āA�@�����P�R�@�@�i�I�j
�@Dengan kesaktian Indukmu ����̃R�����g�ł��B�i�ߘa�S�N�U���X���t���j
�@���̖��̍��̔w�i�ɂ́A�u�Ԍ��E���É��E���O�v������̂��Ǝv���܂����B
�@��̓I�ɂ́A���̎�̖��Ɋ���Ă���l�ɂƂ��ẮA�s���b�c�d�̊e�ӂ̒����́A�u����
���v�ɂȂ��Ă���̂ł́t�ƁA�A�^�������Ƃ������ƂɂȂ�܂��B
�i���@�Q�l�F�u�ӂƊp�̔������W�U�v�j
�@�炷���邳��̃R�����g�ł��B�i�ߘa�S�N�U���X���t���j
�@(5^2+8^2-7^2)/(2*5*8)=1/2�@�Ƃ����v�Z����A3�ӂ� 5�A7�A8 �̎O�p�`�� 5 �� 8 �̕ӂŋ�
�܂��p�̊p�x��60���Ƃ킩��B(���m�Ƃ���Όv�Z�s�v)
�@�}�̌`�́A�R�ӂ� 5�A7�A8 �̎O�p�`�� 5 �̕ӂ� 8 �̕ӂ̊O���ɁA���ꂼ�ꐳ�O�p�`��
���������`�Ȃ̂ŁA�@AB=5+8=13�B
�@�f�`�h ����̃R�����g�ł��B�i�ߘa�S�N�U���X���t���j
�@�}�ł� AD=a�ABC=b�ACD=c�AAB=x �Ƃ����āA���̂S�������ƂȂ��g�������ׂ���A
(a,b,c)=(1,4,7)�@->�@x=9
�@�@�@ =(2,5,7)�@->�@x=10
�@�@�@ =(3,6,7)�@->�@x=11
�@�@�@ =(4,7,7)�@->�@x=12
�@�@�@ =(5,8,7)�@->�@x=13
�@�@�@ =(6,9,7)�@->�@x=14
�@�@�@ =(7,10,7)�@->�@x=15
�@�@�@�@�������������
�@��ʂɁA�@(a,b,c)=(n,n+3,7)�@->�@x=n+8�@(n=1,2,3,���)
�܂��́A
(a,b,c)=(1,6,7)�@->�@x=9
�@�@�@ =(2,7,7)�@->�@x=10
�@�@�@ =(3,8,7)�@->�@x=11
�@�@�@ =(4,9,7)�@->�@x=12
�@�@�@ =(5,10,7)�@->�@x=13
�@�@�@ =(6,11,7)�@->�@x=14
�@�@�@ =(7,12,7)�@->�@x=15
�@�@�@�@�������������
�@��ʂɁA�@(a,b,c)=(n,n+5,7)�@->�@x=n+8�@(n=1,2,3,���)
�@c=7 �Ɛݒ肵�Ă������Ƃ��|�C���g�ɂȂ肻���ł��B
�i�R�����g�j�@�f�`�h �����ׂ�ꂽ�A���낢��ȃp�^�[���A�Q�l�ɂȂ�܂��B������p����
�@�@�@�@�@�@���o�������ł��B
�@DD++ ����̃R�����g�ł��B�i�ߘa�S�N�U���P�O���t���j
�@c=13 �� c=19 �ł��\�Ȃ̂ł́B�����炭�A6n+1 �^�f���������Ȃ��Ƃ� 1 �����Ă��邱��
����������Ȃ��ł��傤���B
�i�R�����g�j�@�Ⴆ�A(a,b,c)=(15,8,13)�@���Ɓ@x=23�@�ƒ�܂�܂��ˁI�炷���邳��́u���O�p
�@�@�@�@�@�@�`�����������`�v���l����A�ȒP�ɁA�����������悤�ł��B
�@AD=a�ABC=b�ACD=c�AAB=x=a�{b �ɂ����āA
�@�@��2����2�{��2�|����
�����藧�悤�ɁA���� ���A���A�� ���߂�悢�B
�@�f�`�h ����̃R�����g�ł��B�i�ߘa�S�N�U���P�P���t���j
�@�m���ɁA6*n+1�^�̐��́A
7^2=3^2+8^2-3*8=5^2+8^2-5*8
13^2=7^2+15^2-7*15�@=>�@(a,b,c)=(n,n+8,13)�@->�@x=n+15�@(n=1,2,3,��)
13^2=8^2+15^2-8*15�@=>�@(a,b,c)=(n,n+7,13)�@->�@x=n+15�@(n,1,2,3,��)�@���\���ł���B
19^2= 5^2+21^2- 5*21�@=>�@(a,b,c)=(n,n+16,19)�@->�@x=n+21�@(n=1,2,3,��)
19^2=16^2+21^2-16*21�@=>�@(a,b,c)=(n,n+5,19)�@->�@x=n+21�@(n=1,2,3,��)
25^2=25^2+25^2-25*25(����͗�O�j
31^2=11^2+35^2-11*35�@=>�@(a,b,c)=(n,n+24,31)�@->�@x=n+35�@(n=1,2,3,��)
31^2=24^2+35^2-24*35�@=>�@(a,b,c)=(n,n+11,31)�@->�@x=n+35�@(n=1,2,3,��)
�@�ȉ����l
37^2= 7^2+40^2-7*40=33^2+40^2-24*40
43^2=13^2+48^2-13*48=35^2+48^2-35*48
49^2=16^2+55^2-16*55=39^2+55^2-39*55
�@�@����������
�ƁA60���̊p�x��L����O�p�`�̎O�ӂ�^���Ă����Q�g��^���Ă���܂��ˁB