正三角形は作れる？　　　　　　　　　 　　　　　　　　　　　　　　　

　幾何の問題において、「等積変形」という言葉は有名である。（→　参考：「四角形の分割」）

　等積変形


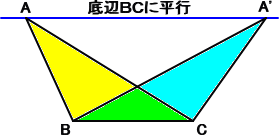
　　　左図において、

　　　　　△ＡＢＣ＝△Ａ’ＢＣ

　　　が成り立つ。



　数学セミナー　’１８　２月号（日本評論社）の中の「エレガントな解答をもとむ」で、この話題
が取り上げられている。

　ウォーミングアップ問題で、

　任意の三角形は、等積変形を何回か行うことにより、正三角形にできる

とのことであるが、どうすればいいのだろうか？２等辺三角形を作る操作を無限回行えば、
その極限として正三角形に近づく雰囲気はあるのだが、問題文で「何回か」とあるので、きっ
と有限回の操作でできるのだろう。いや〜、新年早々難しいですね！

　なお、この問題は、数学セミナー　’８６年　１月号（日本評論社）の中の「エレガントな解答
をもとむ」で出題されたものらしい。

















（答）　らすかるさんが考察されました。（平成３０年１月１５日付け）

　三角形を△ABCとする。Cを中心としてBを通る円Cを描く。Bを中心としてCを通る円Bを描
き、円Cとの交点をD、Eとする。ただし、BCに関してAと同じ側にある方をDとする。

　Eを中心としてB、Cを通る円Eを描き、円Bと円Eの交点のうちCでない方をF、円Cと円Eの
交点のうちBでない方をGとする。

　Aを通りBCに平行な直線と直線CDの交点をHとする。GHを直径とする円と直線CFの交点
をIとする。

　Cを中心としてIを通る円と直線CD、CBとの交点をJ、Kとすれば、△CJKは△ABCと面積
の等しい正三角形。

　　　　　　　

（コメント）　上記の考察で、等積変形がどう絡むのか、ちょっと不明．．．。


　とあるAKBファン（だった）さんからのコメントです。（平成３０年１月１８日付け）

　△ABCの面積が求められれば、同じ面積の正三角形の1辺の長さがわかるので等積変形
２回でいけます。

　今回は、Cを中心としてIを通る円の半径が等積正三角形の1辺の長さなのでこれを使いま
しょう(J、Kは使いません)。

　Aを通り、BCに平行な直線とCを中心としてIを通る円の交点の1つをLとすると、
△ABC=△LBCと等積変形できる。

　Lを中心として、Cを通る円とCを中心としてIを通る円の交点のうち、LCに対してBと同じ側
にある点をMとすると、△LMCは正三角形となり、これは、らすかるさんの作図方法が正しけ
れば、△ABC=△LBCと面積が等しいはずである。(←えっ)

　よって、△LBC=△LMCであり、これは等積変形となる。

という感じの作図手順でいかがでしょうか？

追記：Aを通りBCに平行な直線とCを中心としてIを通る円が交わらない場合があるので、そ
　　　の場合はAとBを読み替えてください。どちらかの操作で必ず正三角形ができるはずで
　　　す。(未検証)


　らすかるさんからのコメントです。（平成３０年１月１８日付け）

　疑問に思っていたのですが、そもそもこの問題の「等積変形」というのは何を指しているの
でしょうか。

　例えば、「四角形の分割」の一番下にある「長方形と同じ面積を持つ正方形を作る」の作図
は「等積変形」ではないのでしょうか。

# 「等積変形」について検索してみると、「図形の面積を変えずに形を変えること」と出てきま
　すので、私はこれも「等積変形」だと思っているのですが．．．。

　もし「等積変形」が、「三角形の頂点を、対辺に平行に移動させて同じ面積の三角形を作る」
という操作のことだけを指しているとしたら、この操作を有限回使って同じ面積を持つ正三角
形をどこかに作ることが目的になりますよね。

　で、とあるAKBファン（だった）さんも書かれていますが、辺の長さがわかれば、当然その「等
積変形」でも変形できるわけです。

　しかし、私の作図法で辺の長さがわかった時は、既に60°の角度もありますので、そこに
２辺をとってしまえば、同じ面積を持つ正三角形は出来てしまって目的が達成されるわけで、
わざわざここから辺の長さだけを使って元の図形を「等積変形」する意味はないだろうと思っ
てあの作図で終わりにしたということです。

＃　任意の多角形の「等積変形」について、

　「同じ面積を持つ目的の図形が作図可能」

⇔「『三角形の頂点を、対辺に平行に移動させて同じ面積の三角形を作る』という操作で目的
　　の図形に変形可能」

が成り立つと思います。


（コメント）　問題設定が舌足らずだったようで、ご心配をおかけしました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成３０年１月１９日付け）

　「等積変形」は、「三角形の頂点を、対辺に平行に移動させて同じ面積の三角形を作る」と
いう操作を意図していました。出典の数学セミナーでは、この操作を「 Ｉ-変形」と呼び、「 Ｉ-変
形」を何回か使って正三角形を作る手順を求めています。この部分を私が勝手に「等積変形」
と一括りにしてしまったので、誤解が生じたようです。申し訳ありませんでした。


　らすかるさんからのコメントです。（平成３０年１月１９日付け）

　了解致しました。それでは、図で、線分BJ、線分HKを書いて頂ければ、

(1)　△ABC→△HBCの「等積変形」
(2)　△BKH→△JKHの「等積変形」
　※ただし、HC＞BCの場合は△HBJ→△KBJの「等積変形」

により、２回(以下)の「等積変形」で可能なことがわかると思います。

　　　　　　

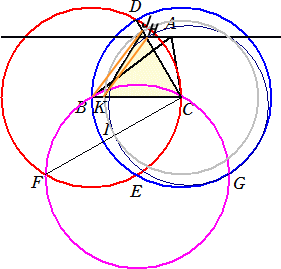
（コメント）　お〜、なるほど！らすかるさんに感謝します。


　DD++さんからのコメントです。（平成３０年１月１９日付け）

　「四角形の分割」の長方形を正方形にするのは等積変形ではないですよね。長方形と同じ
面積を持つ正方形を「作る」と言っている通り、ただ等積な図形を「改めて隣に作った」だけ
ですし。

　これと変形との違いは、最初の図形と最後の図形が連続的につながっているか、ですね。

　加えて言えば、今回は作図手順は要求されていません……というか、作図可能性の要求
すらありません。つまり、期待された解答はこういう感じのものだったのではないでしょうか？

1. 三角形の辺のうち、もっとも短い辺を仮にABとする。それは目的の正三角形の辺の長さ
　より短いはずである。
2. 点Aを等積変形で動かしていく。
3. 点Aが無限に遠くにいくまでに、ABの長さが目的の正三角形の辺の長さになる瞬間があ
　るはずなので、そこで点Aを止める（A'とする）
4. 点Cを等積変形で、A'Bの垂直二等分線上に移動する


　らすかるさんからのコメントです。（平成３０年１月１９日付け）

　 「四角形の分割」の長方形を正方形にするのも「等積変形」と言っている人がたくさんいま
すので、私は等積変形だと思います。

http://izumi-math.jp/sanae/MathTopic/touseki/touseki.htm
http://math.a.la9.jp/atous.htm
http://www13.plala.or.jp/isemba/PUZZLE/p521.pdf

　あと、図形を切って組み直すのも「等積変形」に含めているサイトが多いです。「作図で形
が違う同じ面積の図形を作る」、「図形を切って組み立て直し、形を変える」、「三角形の頂
点を対辺と平行に移動して形を変える」はそれぞれ「等積変形」の手段と思っています。

1. 三角形の辺のうち、もっとも短い辺を仮にABとする。それは目的の正三角形の辺の長さ
　より短いはずである。

　一辺が1の正三角形と、1辺が2で2辺が√19/4＞1の二等辺三角形は同じ面積ですので
最短辺が正三角形の辺より短いとは限りませんね。


　DD++さんからのコメントです。（平成３０年１月１９日付け）

　２番目は数学的には平行移動と回転移動で表現でき、連続的な手段ですので、これは私
も「変形」に含めてよいと思います。

　１番目についてはやはり疑問ですね。正方形を改めて作図する方法を等積変形と言わな
いと思っている人は、わざわざ等積変形のページにその方法を書いて「これは等積変形と
は言わない！」と書いたりしないので、この問題で表現が一般的かどうか調査するのは妥
当ではありません。

　むしろ、円積問題について「円を正方形に変形する」と表現している人の割合を調べると、
これを変形と思っている人はかなり少数派なようですよ。

　 一辺が1の正三角形と、1辺が2で2辺が√19/4＞1の二等辺三角形は同じ面積ですので
最短辺が正三角形の辺より短いとは限りませんね。

　あ、本当だ。選んだ辺の隣が鈍角になる方向へ行けば途中で必ず一度正三角形の辺より
短くなるので大きな影響はないですが、実はそういう瞬間は２回あってスタート地点限定だと
辺の長さが正三角形の辺より長い場合もあるんですね。中間値の定理の逆は成り立たない、
と。

　一応ちゃんと修正したのを再掲。

1. 三角形の辺のうち、もっとも短い辺を仮にABとする。
2. 点Aを等積変形で動かしていく。
3. 角Bが直角になるときABは目的の正三角形の一辺より短く、点Aが無限に遠くにいけば
　ABはいくらでも長くなるため、ABの長さが目的の正三角形の辺の長さになる瞬間がある
　はずなので、そこで点Aを止める（A'とする）
4. 点Cを等積変形で、A'Bの垂直二等分線上に移動する

　普通かそうでないか、多数派か少数派か、という話ではなく、きっちり定義された辞書的な
数学用語としての話を調べてみたら、驚きの結果が．．．。

　専門学術用語にも詳しいブリタニカ国際大百科辞典で（コトバンク経由で）調べると、なんと
私もらすかるさんも管理人さんも全員誤りのようです。

　平行線を使って面積が変わらないように図形の頂点を動かすのが「等積移動」、等積移動
の時に頂点が増えたり減ったりで形の種類が変わってしまうのが「等積変形」だそうで．．．。

　三角形の頂点を対辺と平行に動かすのは三角形から三角形なので等積変形じゃないんで
すね。（へぇー。）


　らすかるさんからのコメントです。（平成３０年１月１９日付け）

　そのページには、

・「等積移動」とは平行線を使って面積が変わらないように図形の頂点を動かすことである
・等積移動の時に頂点が増えたり減ったりで形の種類が変わってしまう場合は「等積移動」
　とは言わず「等積変形」という

と書いてあるだけで、「平行線を使って面積が変わらないように図形の頂点を動かすこと」は
「等積変形」とは言わない、とは書かれていませんね。

　ブリタニカで「等積変形」の項目がないようなのでブリタニカの解釈はわかりませんが、少な
くとも「三角形から三角形の変形」を「等積変形」と言っている人は、かなり多いですから、

　　「等積変形」⊃「等積移動」（＝「管理人さんが意図している等積変形」）

と解釈するのが正しいように思います。

＃　分割して組み換えるのも「等積変形」に含める場合は、一般の三角形が有限回の操作
　で正三角形に等積変形できることは、ボヤイの定理から明らかですね。


　DD++さんからのコメントです。（平成３０年１月１９日付け）

　多数派であることは、正しいことの十分条件たり得ません。私もずっとこれを指して等積変
形と言ってきましたし、これからもそう言うと思いますけどね。何にせよ、最初に多数派・少数
派ではなく辞書的な話と最初に断ってあるのに対して、多数派であることを根拠にされまして
も。

　ブリタニカには、「等積変形」⊆「等積移動」であると解釈できる記載があるので、

　　「等積変形」⊂「等積移動」　か　「等積変形」=「等積移動」　か

の議論の余地はあっても、「等積変形」⊃「等積移動」ってことはないでしょう。


　らすかるさんからのコメントです。（平成３０年１月１９日付け）

　 多数派であることは正しいことの十分条件たり得ません。

　一概にそうは言えないと思います。言葉は変化するものですから、単に辞書が時代遅れに
なっている可能性もあります。ブリタニカの辞書に「等積変形」という項目がない以上、他の辞
書や多数派の意見で判断するしかないと思います。

　 ブリタニカには「等積変形」⊆「等積移動」であると解釈できる記載があるので、

　どこか他のページでそのように解釈できる箇所があったのですか？

＃　少なくとも示されたページでは、

　「面積を変えずに三角形が四角形になるような変形」∈「等積変形」
　「面積を変えずに三角形が四角形になるような変形」~∈「等積移動」

と読めますので、「等積変形」⊆「等積移動」はあり得ないと思いますが。


　ハンニバル・フォーチュンさんからのコメントです。（平成３０年１月１９日付け）

　辞書的な話で言えば、デジタル大辞泉の等積変形の項に、例示として以下のようにありま
す。御参考までに。（本当は数学小辞典や現代数学教育辞典あたりを引いてみたいところ
ですが手元にありません。）

　デジタル大辞泉の解説：とうせき‐へんけい【等積変形】

　図形の面積を一定にしたまま、形を変えること。三角形で底辺の長さと高さを同じにしたま
ま、頂点を底辺に対して平行移動させたり、正方形を対角線で二分し、短辺どうしを接して二
等辺三角形にしたりすることを指す。


　DD++さんからのコメントです。（平成３０年１月１９日付け）

　 言葉は変化するものですから、単に辞書が時代遅れになっている可能性もあります。

　もちろんそういう可能性もあります。ご存知だと思いますが、「十分条件ではない」というの
は絶対に偽という意味ではないですよ。私は「それをもって真とはできない」と言っているだけ
で、別に「それをもって偽であるとせよ」などとは言っていません。

　また、何度も言いますが、私はあくまで辞書的な話としてはと前置きをしていることを無視し
ないでください。

　 どこか他のページでそのように解釈できる箇所があったのですか？

　らすかるさん自身で先ほどこうおっしゃってますよ。

　「等積移動の時に」という前提がついている以上、等積移動でなければ等積変形に該当し
ません。「等積変形というのが普通である」というのは別に等積移動といえなくなる意味には
なりませんし。

　 辞書的な話で言えばデジタル大辞泉の等積変形の項に例示として以下のようにあります。

　ほう、そういう記載の辞書もあるんですね。情報ありがとうございます。大辞泉ってこういう
専門用語の信頼性どの程度なんでしょうね？

　本当は数学小辞典や現代数学教育辞典あたりを引いてみたいところですが・・・

　私もこのあたりを引きたいですが、私も手元にないです……。どなたかお持ちの方がいらっ
しゃいればいいのですが。

　等積移動（狭義に平行線を使うやつ）ではなく、図形の切断と再接合で三角形を正三角形
化する手順が気になったのでやってみました。あんまり潰れてない三角形の場合は以下で
可能なようです。

1. 目的の正三角形の辺の長さを頑張って求めておきます。
　（２つの長さの和、差、半分、整数倍、相乗平均は作図できるので、ヘロンの公式の形を
　参考にする等で可能です）

2. 頂点を適当にA,B,Cと命名し、辺ABの中点Mを作図します。

3. 点Mを中心に、目的の正三角形の辺の長さの半分を半径とする円を描きます。

4. その円と辺BCとの交点が以下を全て満たせばそれを点Dとします。
・辺BCのC側半分にある
・∠BMD<120°
・∠BDM<60°
　（三角形が潰れすぎていると、A,B,C と頂点の対応6通りのどれでも点Dが取れない場合が
　あります）

5. 辺ACの中点Nを作図します。

6. 点Nを通り線分MDに平行な直線を引き、辺ABとの交点をEとします。
（4.の「辺BCのC側半分にある」条件から、きちんと辺上で交わります）

7. 点Mに関して点Eと対称な点Fを作図します。

8. 点Fを通り線分MDに平行な直線を引き、辺BCとの交点をGとします。
　（線分FG、線分MD、線分ENが等間隔の平行線になります）

9. 線分MDを一辺とする正三角形MDHを作図します。2つ描けるうち、点Hが線分EN上に来る
　方を採用します。
　（4.の「∠BMD<120°」「 ∠BDM<60°」から、延長上ではなくきちんと線分上に来ます）

10. 三角形を、線分FG、線分MH、線分DH、線分ENで5分割します。

11. 点M、点G、点D、点N を軸にして、鳩目返しっぽく「せーの」で回転させると正三角形にな
　ります。

　長辺が短辺の√3倍以下である長方形から正三角形への鳩目返しを考えて応用したので
すが、長方形と三角形の差異の分△BFGが変なところにいってしまい、ちゃんとした鳩目返
しになっておらず、「ぽい」だけというオチに……


　らすかるさんからのコメントです。（平成３０年１月１９日付け）

　DD++さん、無視しているつもりはありませんが、辞書的な話といっても辞書に載っていない
ものは（その）辞書では解釈のしようがないと思います。ブリタニカだけで解釈するならば「等
積変形」の範囲はわかりませんね。

　 「等積変形というのが普通である」というのは別に等積移動といえなくなる意味にはなりま
せんし。

　これはわかりました。確かにそのように解釈できます。しかし、

　 「等積移動の時に」という前提がついている以上、等積移動でなければ等積変形に該当
しません。

　これは言えないと思います。等積移動に該当しない図形の切り貼りなども等積変形に含ま
れる可能性があります。ブリタニカのこの項目では「等積変形はこれだけだ」とは言っていま
せん。しかも、等積移動のうち「等積変形というのが普通である」もの以外は等積変形では
ない、とも書いてありませんので、ブリタニカだけでは、

　　「等積変形」⊂「等積移動」　か　「等積変形」⊃「等積移動」　か

の判断はできません。今までの情報をまとめると、（とりあえず、長方形と同面積の正方形を
作図するのは除外して）

・図形の切り貼りで形を変えるもの→等積変形ではあるが、等積移動ではない

・平行移動で三角形を形の異なる三角形に変換
　　　　　　　　　　　　　　　　　　　　　　→等積変形でも等積移動でもあり、どちらの用語も使う
（ブリタニカの等積移動に含まれるが、等積変形でないとはどこにも書かれていないし、一般
的に考えて等積変形には含まれるはず）

・平行移動で四角形を三角形に変換→等積変形でも等積移動でもあるが、普通等積移動と
　　　　　　　　　　　　　　　　　　　　　　　は言わない
　　（ブリタニカの記述通り）

　よって、「等積変形」⊃「等積移動」と考えれば、ブリタニカを含めどこにも矛盾しないと思う
のですが、いかがでしょうか。

# 厳密な定義が見当たらない言葉について掲示板上で議論しても厳密な結論が出るわけで
　はないので、あまり意味がないんですけどね…


　DD++さんからのコメントです。（平成３０年１月１９日付け）

　 ブリタニカだけで解釈するならば「等積変形」の範囲はわかりませんね。

　一般的な書籍ならともかく、辞書や辞典の類のものならどこにも言及がない=存在しないと
解釈していいんじゃないかと思いますがどうでしょう？使用頻度の低い語というわけでもない
ですし。

・図形の切り貼りで形を変えるもの→等積変形ではあるが、等積移動ではない

　これもどうなんでしょう？等積移動でない方は明白です。広義に等積変形でひとまとめに
扱ってしまうことが多いのも事実ですが……狭義にはこれは含んでいるのでしょうか？

・平行移動で三角形を形の異なる三角形に変換
　　　　　　　　　　　　　　　　　　　　　　→等積変形でも等積移動でもあり、どちらの用語も使う

　わざわざ「形が四辺形から三角形というように他の図形に変るときは」のように断りを入れ
て説明している場合、自然言語としては（特に辞書の記載では）単なる "if" ではなく "if and
only if" を意味することが多いので、同種の図形になる場合について触れられていない=そ
う呼ぶことはないと解釈していいと思います。広義にこれも含んで使ってしまうことが多い
（実際に私はそう使っていた）ですが、狭義にはどうなんですかね？

# 厳密な定義が見当たらない言葉について掲示板上で議論しても厳密な結論が出るわけで
　はないので、あまり意味がないんですけどね…

　これは間違いないですね。とはいえ、我流定義のバラバラさが思っていた以上だったという
発見があったので、全く無価値な議論というわけでもなかったですが。今後使うときには気を
つけよう。

　数学用語専門の辞典には厳密な定義が載ってるんでしょうか？

# 自然数に0を含むか否かみたいに派閥がある可能性もありそう。


　とあるＡＫＢファン（だった）さんからのコメントです。（平成３０年１月２０日付け）

　DD++さんの

1. 三角形の辺のうち、もっとも短い辺を仮にABとする。
2. 点Aを等積変形で動かしていく。

　私は最短辺の片方の頂点ではなく最長辺の向かい側の頂点で考えてました。というのも
三角形の面積は底辺×高さなので(この問題における“等積変形”の根本原理ですね)、最
長辺を底辺とすればその三角形の高さが目的の正三角形より低いことが確実だからです。
操作自体は全く同じだね、とか突っ込まれそうですが、考え方の根拠ということで。

＊これにこだわってたせいで、らすかるさんの回答にある「△BKH→△JKH」がまったく見え
　てませんでした……(中学受験レベルなのに忘れるものは忘れますね。)

（本当は数学小辞典や現代数学教育辞典あたりを引いてみたいところですが手元にありま
せん。）

　この論文に言及がありました。（以下引用。中略なども引用文のまま）

　筆者は、教師向けの明確な記述を算数教育・数学教育の論文・書籍等で見かけることが
なかった。更に、等積変形の明確な定義をも見かけることがなかった。等積移動・等積変形
について、「数学小辞典」([4], p.407)は次のように記述している。

　『面積を変えないで、形を変えること。例えば、…（中略）…。等積移動というときには三角
形なら他の形の三角形で面積が同じものに移すことを意味し、四角形を面積の等しい三角
形に直す様な場合は等積移動という。』

　また、「現代数学教育辞典」([3], p.533)は次のように記述している。

　『…このように、平行線間の距離が等しいことを使って、面積の等しいちがった形の図形を
作ることを等積変形という。』

(「現代数学教育事典」の索引には等積移動の項目はない。最近は、等積移動を等積変形と
一括しているようである。)


　DD++さんからのコメントです。（平成３０年１月２０日付け）

　とあるAKBファン（だった）さん、おお、よく見つけられましたね。ブリタニカや大辞泉はこれ
らを引用していたものですか。
（あるいは、これらも共通の何かから引用しているかもしれませんが）

　4.等積変形の定義 の内容や 6.終わりに の最後三行でも言及がありますね。

　それらも含めてまとめると、

・平行線を用いて同じ面積の同種の形にするのが「等積移動」
・図形の一部を等積移動することで、全体を同じ面積の異種の形にするのが「等積変形」
・上記が本来の意味らしいが、正確に定義されたものというわけでもないらしい
・等積移動も含めて広義に等積変形と言うことも増えている

ということになりますかね。


（コメント）　ありがとうございます。今まで何とはなしに使っていた「等積変形」ですが、意味
　　　　　　がはっきりして感謝です。結論的には、今までのままでよいということで．．．。