四角形の分割　　　　　 　　　　　　　　　　　　　　　　　　　

　幾何の問題において、「等積変形」という言葉は有名であるが、その意外な使い方に今日
初めて気がついた。作図問題においても、この等積変形が活躍するとは、ただ驚くばかりで
ある。

等積変形

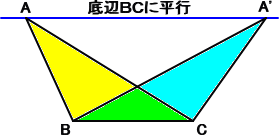左図において、 　　　　　△ＡＢＣ＝△Ａ’ＢＣ 　　　が成り立つ。

　このページでは、次のような問題を考える。

問題　　一般の四角形を頂点を通る直線で等分割したい。どのように直線を引けばよいか？

　

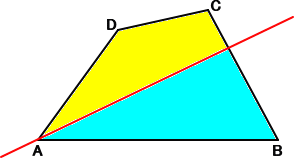
　　　【黄色い部分の面積＝水色の部分の面積】

　この問題に対して、直線を、次のように作図すればよい。

対角線ＢＤの中点を、Ｅ とする。さらに、Ｅ を 　　通り、対角線ＡＣに平行な直線ＦＧを引く。 　　このとき、直線ＡＧが求める直線である。 　　　実際に、△ＡＢＥ＋△ＢＣＥは、四角形の面積 　　の半分であるが、等積変形により、左図におい 　　て、黄緑色の部分は、同じ面積である。

　　よって、△ＡＢＥ＋△ＢＣＥ＝△ＡＢＧ　が成立。

（補足）　△ＡＢＥ＋△ＢＣＥが、四角形の面積の半分であることは、

　　△ＡＢＥ＝△ＡＤＥ　、　△ＢＣＥ＝△ＤＣＥ

から明らかであろう。これは、高さの等しい２つの三角形の面積比は底辺の長さの比に等し
いことから分かる。

　この事実を効果的に用いる問題が、平成２１年９月１３日放送の「熱血！平成教育学院」
（ＮＴＶ系）で出題された。

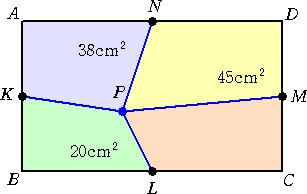長方形ＡＢＣＤ内の点Ｐと各辺の中点 　　を結び四角形を分割したら、左図のよう 　　な面積となった。このとき、 　　四角形ＰＬＣＭの面積を求めよ。

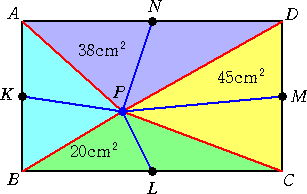
　この問題に対して、右図のような補助線を引いて考えることがポイントとなる。

右図において、 　四角形ＰＬＣＭ ＝四角形ＰＫＢＬ＋四角形ＰＭＤＮ 　−四角形ＰＮＡＫ ＝４５＋２０−３８ ＝２７（ｃｍ2）

（コメント）　一瞬求められそうにないような雰囲気ですが、図形の性質を上手く使うと、こん
　　　　　　なにも鮮やかに解けるんですね！


（追記）　冒頭の問題では直線が頂点を通る場合であったが、より一般な場合はどうであろ
　　　　　うか？それが次の問題である。

問題　　一般の四角形を、辺上の１点を通る直線で等分割したい。どのように直線を引けば
　　　　よいか？
　　　

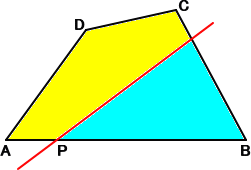
　【黄色い部分の面積＝水色の部分の面積】

　この問題に対して、直線を、次のように作図すればよい。

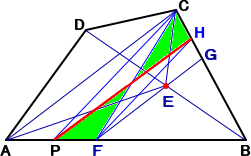対角線ＢＤの中点を、Ｅ とする。 　　 Ｅを通り、対角線ＡＣに平行な直線ＦＧを引く。 　　 直線ＰＣに平行な直線ＦＨ を引く。 　　 このとき、求める直線は、直線ＰＨ である。

　　実際に、△ＡＢＥ＋△ＢＣＥは、四角形の面積の半分であるが、等積変形により、

　△ＡＦＥ＝△ＣＦＥ　なので、　△ＡＢＥ＋△ＢＣＥ＝△ＢＣＦ　である。

　上図において、等積変形により、黄緑色の部分は、 同じ面積である。

　　したがって、△ＢＣＦ＝△ＰＢＨ　が成立。

（再追記）　同様の問題が三角形においても考えられる。

問題　　一般の三角形を、辺上の１点を通る直線で等分割したい。どのように直線を引けば
　　　　よいか？
　　　

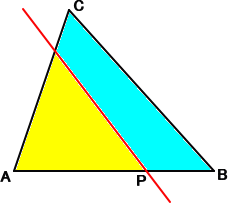
　【黄色い部分の面積＝水色の部分の面積】

　この問題に対して、直線を、次のように作図すればよい。

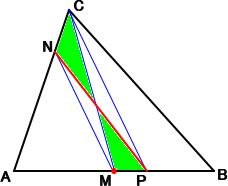底辺ＡＢの中点をＭとし、直線ＣＰに平行な直線ＭＮ 　を引く。 　　このとき、求める直線は、直線ＰＮ である。 　　実際に、△ＡＭＣは、三角形の面積の半分であるが、 　等積変形により、左図において、黄緑色の部分は、同 　じ面積である。 　　したがって、△ＡＭＣ＝△ＡＰＮ　が成立。

（注）　辺上の１点を通る直線を ｎ−１ 本引いて、面積を ｎ 等分したい場合は、辺ＡＢを ｎ
　　　等分して、上と同様に作図すればよい。

問題　　一般の三角形を、１つの辺に垂直な直線で等分割したい。どのように直線を引けば
　　　　よいか？
　　　

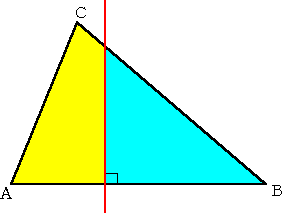
　　【黄色い部分の面積＝水色の部分の面積】

　この問題に対して、直線を、次のように作図すればよい。

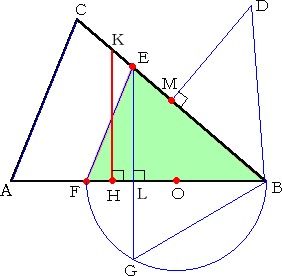辺ＢＣの中点Ｍにおいて、長さＢＭの垂線ＭＤ を引く。辺ＢＣ上に、ＢＥ＝ＢＤとなる点Ｅをとる。 　辺ＡＣに平行な直線ＥＦを引く。線分ＢＦを直径 とする半円Ｏを描き、その円周上に点Ｇを、 辺ＡＢと線分ＥＧが垂直になるようにとる。辺ＡＢ 上に、ＢＨ＝ＢＧとなる点Ｈをとる。 　このとき、点Ｈにおける垂線ＨＫが求める垂線 である。

　実際に、ＢＣ²：ＢＥ²＝２：１　なので、△ＢＥＦは、三角形の面積の半分である。

また、△ＢＦＧは直角三角形で、線分ＧＬは、斜辺ＢＦの垂線なので、△ＢＬＧ∽△ＢＧＦ　が

成り立つ。よって、　ＢＧ²＝ＢＦ・ＢＬ　が成り立つ。

　このとき、△ＢＫＨ：△ＢＥＬ＝ＢＨ²：ＢＬ²＝ＢＧ²：ＢＬ²＝ＢＦ・ＢＬ：ＢＬ²＝ＢＦ：ＢＬ　である。

ところで、△ＢＥＦ：△ＢＥＬ＝ＢＦ：ＢＬ　なので、したがって、△ＢＫＨ＝△ＢＥＦ　が成り立つ。


問題　　一般の三角形の面積を、平行な２直線で３等分に分割したい。どのように直線を
　　　　引けばよいか？

　　

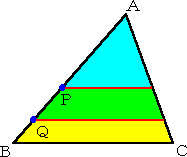
　この問題に対して、直線を、次のように作図すればよい。

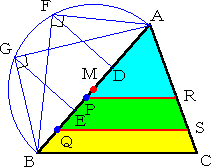辺ＡＢの中点Ｍにおいて、半径ＡＭの半円を描く。 　　辺ＡＢを３等分し、その等分点Ｄ、Ｅにおける垂線と 　半円との交点を、Ｆ、Ｇとする。 　辺ＡＢ上に、ＡＰ＝ＡＦ、ＡＱ＝ＡＧ　となる点Ｐ、Ｑを 　とる。

　２点Ｐ、Ｑにおいて、辺ＢＣと平行な直線ＰＲ、ＱＳを引く。この２直線がもとめるものである。

　実際に、ＡＢ＝３　とすると、１：ＦＤ＝ＦＤ：２　より、ＦＤ²＝２　なので、ＡＰ²＝ＡＦ²＝３

　同様にして、ＡＱ²＝ＡＧ²＝６

このとき、△ＡＰＲ：△ＡＱＳ：△ＡＢＣ＝ＡＰ²：ＡＱ²：ＡＢ²＝３：６：９＝１：２：３

　よって、直線ＰＲ、ＱＳは、△ＡＢＣの面積を、３等分している。


　次の２つの問題は、面積の分割とは違うが、等積図形をうまく図形に組み合わせて、
１つの図形を形作るという意味で、同じ範疇の問題と考えていいだろう。

問題　　一般の三角形において、同じ面積をもつ平行四辺形を作れ。

　

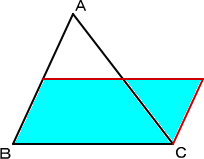
　この問題に対して、次のように作図すればよい。

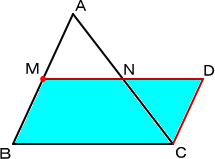辺ＡＢの中点をＭとし、平行四辺形ＭＢＣＤを作れ 　　ばよい。 　　　実際に、辺ＭＤと辺ＡＣの交点をＮとすると、 　　△ＡＭＮ≡△ＣＤＮ　で、面積は等しい。

問題　　一般の平行四辺形において、同じ面積をもつ別の平行四辺形を作れ。

　　

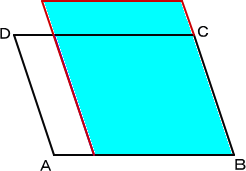
　この問題に対して、次のように作図すればよい。

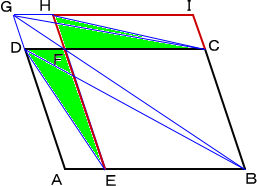辺ＡＢ上の任意の点Ｅにおいて、辺ＡＤと平行 　な直線が辺ＣＤと交わる点をＦとする。ＢＦの延 　長とＡＤの延長との交点をＧとする。平行四辺形 　ＡＢＩＧにより、点 Ｉ を決める。平行四辺形ＦＣＩＨ 　により、点Ｈを決める。 　このとき、平行四辺形ＥＢＩＨが求めるものである。

　実際に、等積変形により、左図において、黄緑色の部分は、同じ面積なので、明らか。


　次の問題も、面積の分割とは違うが、等積図形を作る方法としては面白い。

問題　　一般の長方形において、同じ面積をもつ正方形を作れ。

　　

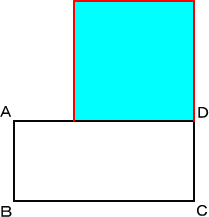
　この問題に対して、次のように作図すればよい。

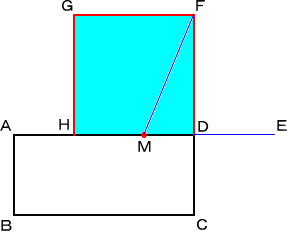ＡＤの延長上に、ＤＣ＝ＤＥ　となる点Ｅ をと 　る。線分ＡＥの中点を、Ｍとする。Ｍを中心と 　する半径ＡＭの半円とＣＤの延長との交点を 　Ｆとする。 　このとき、正方形ＤＦＧＨが求めるものである。

　実際に、左図において、　ＡＢ＝２ａ、ＢＣ＝２ｂ　とすると、ＭＤ＝ｂ−ａ

　ＦＭ＝ＥＭ＝ａ＋ｂ　なので、ＦＤ²＝（ａ＋ｂ）²−（ｂ−ａ）²＝４ａｂ

　よって、長方形と正方形の面積は等しい。

（参考文献：野口健助　著　平面画法入門（日刊工業新聞社））


（追記）　令和３年３月２４日付け

　等積変形にまつわる問題を考えてみた。

問題　　平行四辺形ＡＢＣＤにおいて、ＡＤ＝１０ とする。さらに、ＢＣ上に点Ｐをとり、ＢＰ＝４
　　　　とする。直線ＤＰと直線ＡＢの交点をＱとおく。

　　　△ＡＰＱ＝２０ のとき、平行四辺形ＡＢＣＤの面積を求めよ。

　　

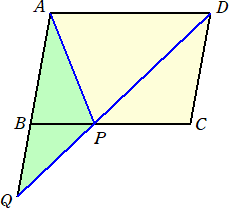
（解）　下図のように等積変形を行う。

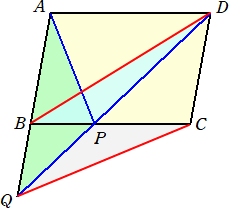△ＡＢＰ＝Ｓ とおくと、△ＡＢＰ＝△ＤＢＰ＝△ＣＰＱ＝Ｓ 　よって、　△ＢＱＰ＝（２/３）Ｓ　より、　（５/３）Ｓ＝２０ なので、Ｓ＝１２　即ち、△ＡＢＰのＢＰを底辺とする高さは 　１２×２÷４＝６　となる。 以上から、平行四辺形ＡＢＣＤの面積は、６×１０＝６０