
 左図のような1辺の長さが1の正方形を、8個の小正方
左図のような1辺の長さが1の正方形を、8個の小正方形に分割したい。
小正方形の大きさは、それぞれ異なってもよい。どのよ
うに分割すればいいだろうか?
(答)
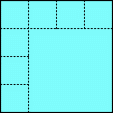 とか、
とか、 が考えられる。
が考えられる。1辺の長さが1だと考えにくいので、4×4 の正方形とすると、前者が得られる。5×5 の
正方形として、25という数字を平方数に分割して、25=32・1+22・3+12・4、・・・・・・・・。
こんなことを考えながら、我が家のお風呂に入って、ピンクのタイルをぼんやり眺めていた
ら、後者が思い浮かんだ。6×6、7×7の正方形も検討したが、答は見い出せなかった。
もっと検証すれば、さらに答があるかもしれない。他の解を見つけられた方、こちらまでメ
ール下さい。
(追記) 後者の変形として、次の場合も考えられる。




パズルが好きな方に、この問題を検証してもらった。「8個の小正方形への分割」は、お
そらく上記の6種類だろうとのこと。もっと違うタイプが見つかったら、こちらまでメール下さ
い。
(追記) 上記の問題に関連して、いくつか考察してみた。(平成25年6月23日付け)
正方形をいくつかの小正方形に分割と聞いたら、すぐ「対辺の中点同士を結んで分割され
た4つの小正方形」を思い浮かべる方が多いと思う。
ところで、「2つの小正方形」に分割できないことは図形的に納得できるが、「3つの小正方
形」に分割できるかどうか、多分できないと思われるが悩ましい。「不可能の証明」の岡 潔先
生の心境だ。また、「5つの小正方形」に分割できるか?と問われると、即答は難しい。
(追記) 平成26年3月19日付け
上記で、「『3つの小正方形』に分割できるかどうか、多分できないと思われるが悩ましい。」
と吐露しましたが、次のようにして示されることに最近気づかされた。
(証明) 起こりえるのは、大きな小正方形の上に、合同な小正方形が2つ並ぶ場合である。
このとき、合同な2つ小正方形が存在する限り、3つの小正方形を組み合わせた図形が
正方形になることはない。
よって、正方形を3つの小正方形に分割することは不可能である。 (証終)
「『5つの小正方形』に分割できるか?」という問いかけに対して、当HP読者のHN「Y.I.」
さんが否定的に解決されました。一部文言等を修正させていただきました。よろしくご了承く
ださい。(平成26年3月18日付け)
(証明) 正方形を5つの正方形に分割できると仮定する。元の正方形の辺の長さをnとする。
隅にある4つの正方形A、B、C、Dのそれぞれの辺の長さを、a、b、c、d とする。
5つ目の正方形Eは、元の正方形の辺に接しているか、接していないかのどちらかである。
・接している場合
Eは、2つ以上の辺に接していることはない。
実際に、Eが、2つ以上の辺に接しているとするとき、残りのスペースを埋めるには、対称
性から、必ず奇数個必要なので、4個(偶数個)の小正方形で埋め尽くすことは不可能であ
る。
そこで、Eは、1つの辺に接しているものとする。対称性により、EはAとBの間にあると考え
てよい。
Eの辺の長さをeとすると、 a=b=e で、c=d=2e とならなければならないが、4e=3e 即ち
e=0 となり、これは矛盾である。
・接していない場合
この場合、a+b=b+c=c+d=d+a=n が成り立つ。a+b=b+c より、a=c。同様に、b=d。A、B、C、D
の面積の合計は、2a2+2b2 ・・・ (1)
一方、元の正方形の面積は、(a+b)2 = a2+2ab+b2 ・・・ (2)
よって、Eの面積は、(2) -(1)より、2ab-(a2+b2)=-(a - b)2<0 となる。これは矛盾である。
(相加・相乗の平均の関係から、a2+b2≧2√(a2b2)=2ab としてもよい。)
つまり、5つの小正方形への分割は不可能である。 (証終)
ところで、「6つの小正方形」、「7つの小正方形」に分割できることは明らかだろう。


「8つの小正方形」に分割できることは上記の問題から明らかである。
YI さんからのコメントです。(平成26年3月20日付け)
「分割パズル」について、2・3・5個への分割が不可能なことがわかりましたが、それ以外
の個数への分割は必ず可能なことがわかりました。
(証明) 正方形をn個に分割できると仮定する。元の正方形を4個に分割(これが可能であ
ることは既知)して、そのうち一つをn個に分割する。すると、全体としては、n+3個に
分割されたことになる。
したがって、n個の分割が可能な時、n+3個への分割が可能である。また、6、7、8
個への分割は可能である。
よって、6以上のすべての整数について分割が可能である。 (証終)
従って、「9つの小正方形」に分割することも当然可能であるが、次の条件を満たす分割方
法を問われたらどうだろう?難易度が急にあがった感じがすると思う。
(1) 1辺の長さが1/3の小正方形をちょうど4個だけ含むような分割方法は如何?
(2) 1辺の長さが1/3の小正方形をちょうど1個だけ含むような分割方法は如何?
(答え) (1) (2)


面積に注目すると、例えば、「対辺の中点同士を結んで分割した4つの小正方形」は、
1=4(1/4)
と表される。上記の「6つの小正方形」、「7つの小正方形」は、それぞれ
1=1(4/9)+5(1/9) 、 1=3(1/4)+4(1/16)
と表される。このように面積に注目すると、直感的に不可能と判断される「2つの小正方形分
割」も、代数的に不可能と示す方法が見つかるかもしれない。
以下、工事中!