当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(令和元年12月30日付け)
「99832769119」は、ある数の立方数である。ある数を求めよ。
(答) 4639
らすかるさんが考察されました。(令和元年12月30日付け)
「ある数」をnとすると、
99832769119≡1 (mod3) から、n≡1 (mod3)
99832769119≡3 (mod4) から、n≡3 (mod4)
99832769119≡4 (mod5) から、n≡4 (mod5)
99832769119≡6 (mod11) から、n≡8 (mod11) (← 83≡-5≡6 (mod11))
n≡1 (mod3)、n≡3 (mod4) から、n≡7 (mod12)
(← 3k+1=4h+3 より、3(k-h)=h+2 なので、h=3m-2 と置ける。即ち、n=4(3m-2)+3=12m-5)
n≡7 (mod12)、n≡4 (mod5) から、n≡19 (mod60)
n≡19 (mod60)、n≡8 (mod11) から、n≡19 (mod660)
99832769119≒99.8×1000^3
4^3=64<99.8<125=5^3 なので、4000^3<99832769119<5000^3
660×6+19=3979、660×7+19=4639、660×8+19=5299 から、「ある数」は、4639
(以上すべて手計算)
(コメント) らすかるさんの求め方は、とても斬新ですね!ちょっと思いつかない方法で勉強
になりました。私は地道に次のように求めました。
(a・103+b・102+c・10+d)3=99832769119 とおける。
mod 10 において、 d3≡9 これを満たすdは、d=9 のみ。
mod 102 において、 (c・10+9)3≡19 より、 30・c+29≡19
これを満たすcは、c=3 のみ。
mod 103 において、 (b・102+39)3≡119 より、 300・b+319≡119
これを満たすbは、b=6 のみ。
mod 104 において、 (a・103+639)3≡9119 より、 3000・a+7119≡9119
これを満たすaは、a=4 のみ。
以上から、求める「ある数」は、 4639
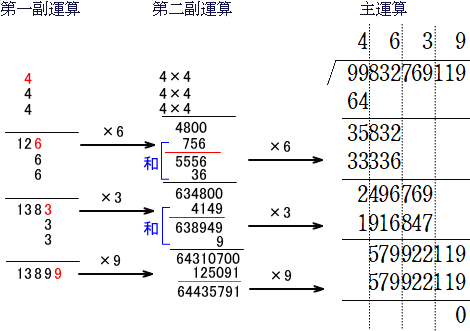
# Excel さんに問いかければ瞬時に答えを返してくれるわけだが、「手計算」を意識すれば
次のようにも求められる。(→ 参考:「平方根・立方根を筆算で求める方法」)