
長方形ABCDにおいて、下図のように点E、F、G、H、I をとる。AHとEC、DGとIFはそれぞ
れ平行である。このとき、黄色い部分の面積を求めよ。
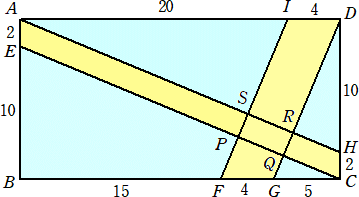
(類題) 面積計算8
(答) 図から明らかに、四角形PQRSは長方形である。∠IAS=θ とおくと、
∠HDR=∠GCQ=θ で、 DG=13 より、 sinθ=5/13 、cosθ=12/13
このとき、 IS=20sinθ=100/13 、AS=20cosθ=240/13 なので、
△ASI=(100/13)・(240/13)・(1/2)=12000/169
同様にして、 HR=10sinθ=50/13 、DR=10cosθ=120/13 なので、
△DHR=(50/13)・(120/13)・(1/2)=3000/169
また、 GQ=5sinθ=25/13 、CQ=5cosθ=60/13 なので、
△CGQ=(25/13)・(60/13)・(1/2)=750/169
FP=9sinθ=45/13 、CP=9cosθ=108/13
CE=26 なので、 PE=26−108/13=230/13
よって、
四角形BFPEの面積=10・15・(1/2)+(45/13)・(230/13)・(1/2)=17850/169
以上から、求める面積は、
12×24−12000/169−3000/169−750/169−17850/169
=15072/169
(コメント) 概数は、89.2位。
2つの帯の面積の和 2×24+4×12=96 には重なりの部分(長方形PQRS)が含ま
れる。
PQ=4cosθ=48/13 、PS=2cosθ=24/13 なので、
長方形PQRSの面積は、 (48/13)・(24/13)=1152/169
よって、求める面積は、 96−1152/169=15072/169 となる。
#求め方としては、こちらの方が楽でした!