
令和2年2月14日(金)に神奈川県公立高校入試が行われ、その問題が翌日の朝刊に
掲載された。面積計算で面白そうな問題があったので挑戦してみた。
平行四辺形ABCDにおいて、AB=15、AD=25とする。Aより辺BCに垂線AEを下ろす。
AD上にAF=15となる点Fをとる。線分BFとAE、ACの交点をそれぞれG、Hとする。
また、∠BAH=90°とする。
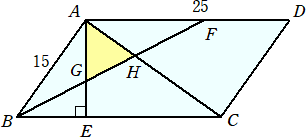
このとき、△AGHの面積を求めよ。(一部改題)
(答)

題意より、 △ABFは2等辺三角形で、 ∠ABF=∠AFB
また、ADとBCは平行なので、∠AFB=∠FBC より、 ∠ABF=∠FBC
よって、BFは∠ABCの2等分線となり、AH:HC=15:25=3:5
AC=20 より、 AH=20×(3/8)=15/2
△BAH≡△FAH なので、 AG=15/2
よって、△BAH=15×(15/2)×(1/2)=225/4 となるので、
△AGH=△BAH+△FAH−△ABF=225/2−△ABF
一方、平行四辺形ABCDの面積は、 15×20=300 なので、
△ABF=150×(15/25)=90
以上から、 △AGH=225/2−90=45/2 となる。 (終)
(コメント) 上記の計算で、角の2等分線の性質を使っているが、この事実を中学生が全員
教わっているのかどうか、少し不安...。もしかしたらもっと別な求め方があるの
かもしれない。
角の2等分線の性質によらない別解を考えてみた。

(別解) AC=20 で、AH:HC=15:25=3:5 より、 AH=20×(3/8)=15/2
よって、△ABH=15×(15/2)×(1/2)=225/4
また、 △ABC=15×20×(1/2)=25×AE×(1/2) より、 AE=12、EC=16
このとき、 AG:GE=15:9=5:3 なので、
△ABG=9×12×(1/2)×(5/8)=135/4
よって、 △AGH=225/4−135/4=90/4=45/2 (終)
(コメント) 中学生向けには多分こちらの方が本解でしょう。
DD++さんからのコメントです。(令和2年2月15日付け)

AG:GE=5:3 、AH:HC=3:5 から、△AGH=(15/64)△AEC=45/2
が作問者の意図した解法でしょうかね。他にもいろんな方法がありそうですけども。
(コメント) なるほど、そういう手もありますね!DD++さんに感謝します。
らすかるさんからのコメントです。(令和2年2月15日付け)

AH:HCは、 △HFA∽△HBC から、AH:HC=FA:BC=3:5 でもいいですね。
他には、
△ABE∽△CBA から、 BE:AE:AB=BA:AC:CB=3:4:5 なので、
BE=9、AE=12
BG:GF=BE:FA=3:5 で、 △ABH≡△AFG から、BG=FH なので、
BG:GH:HF=3:2:3
よって、 △AGH=(GH/BF)△ABF=(1/4)(15×12÷2)=45/2
# これは大きい数が出てきませんので計算しやすいです。
(コメント) 別解もますます磨きがかかって洗練されてきましたね!らすかるさんに感謝しま
す。
よおすけさんからのコメントです。(令和2年2月15日付け)
数学感動秘話「面積比」も参考にどうぞ。
(コメント) 問題の趣旨は全く同じですね!よおすけさんに感謝します。