当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんからの出題です。
（平成２７年４月１日付け）
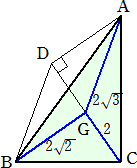
△ABCの重心をGとする。GA＝２
、GB＝２
、GC＝２ のとき、△ABCの面積Sは？また、一般に、△ABCとその重心Gがある。Gから各A、B、Cまでの距離を ｐ、ｑ、ｒ とすると
き、△ABCの面積Sは？
（答え） DD++さんが考察されました。（平成２７年４月１日付け）
まず、一般の場合から。
点Dをとって、平行四辺形AGBDを作り、その対角線交点をEとします。△ABCの面積は、
三角形ABGの面積の３倍なので、それは△ADGの面積の３倍でもあります。
AG＝ｐ、AD＝GB＝ｑ、DG＝２EG＝GC＝ｒ なので、ヘロンの公式より、２ｓ＝ｐ＋ｑ＋ｒ とし
て、△ADGの面積は、√ｓ(ｓ−ｐ)(ｓ−ｑ)(ｓ−ｒ) 即ち、△ABCの面積は、
３√ｓ(ｓ−ｐ)(ｓ−ｑ)(ｓ−ｒ)
三辺の長さが、GA＝２
、GB＝２、GC＝２ その3つの長さだと直角三角形なので、ヘロンの公式よりも普通の公式の方が早いですね。
(２×２
÷２)×３＝６ でしょうか。
DD++さんからのコメントです。（平成２７年４月３日付け）
実は、上記の問題も「空間認識」と結構似たようなことやっていて、
「まず、三角形が潰れた極限を考えると、面積は、0」
「このとき、ｒ が最長だとすると、r=p+q が成り立つ」
「つまり、面積の一般公式は、(p+q-r) を因数にもつ？」
「対称式のはずだから、(q+r-p)も(r+p-q)も因数にもつ？」
「でも、面積は二次相当の式のはず。じゃあ他の面積公式みたいに√（四次式）？」
「この3つの因数に一次の対称式をかけないといけないが、それは(p+q+r)しかないはず」
「あれ、この4つをかけてルートってほぼヘロンの公式そのままだ」
「試しに正三角形で計算すると、どうもヘロンの公式の3倍らしい」
「つまり、与えられた三角形の1/3を等積変形してヘロンの公式を使えば答えが出るのかも
しれない」
「あ、平行四辺形できた」
という思考順序で、上記の解答になってます。