
当HPがいつもお世話になっているHN「よおすけ」さんからの出題です。
(平成25年11月3日付け)
平面上に、AB=12cm、BC=17cmの長方形ABCDがあります。BC上に、BE=5cmとなるよう
な点E、CD上に、FD=7cmとなるような点Fをそれぞれとります。
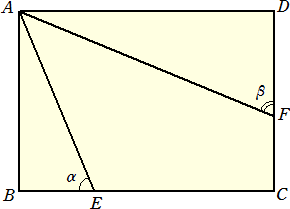
このとき、∠AEB+∠AFDを求めなさい。(→ 類題:「2つの角の和」)
(答) 正接の加法定理を用いれば、何も考えずとも、tanα=12/5、tanβ=17/7 より、
tan(α+β)=(tanα+tanβ)/(1−tanαtanβ)=−1 なので、 α+β=3π/4
と即答できるが、あまりに味気ない。次のような補助線を思いつくのがよおすけさんの出題
のねらいなのだろう。

上図において、明らかに△AEFは直角二等辺三角形なので、∠AFE=45°
よって、 ∠AEB+∠AFD=135°
GAI さんが考察されました。(平成25年11月3日付け)
答えが135°にできる他の長方形 AB=a、BC=b (a<b<20 に限る)と、BE=s、FD=t の長
さの組合せを調査しました。
a/s;b/t=2/1;3/1 3/2;5/1 4/1;5/3 4/3;7/1 5/2;7/3 5/4;9/1 6/1;7/5 7/2;9/5 7/4;11/3
8/1;9/7 8/3;11/5 8/5;13/3 9/2;11/7 9/4;13/5 10/1;11/9 10/3;13/7 10/7;17/3
11/2;13/9 11/4;15/7 11/6;17/5 11/8;19/3 12/5;17/7(本問題) 12/7;19/5
13/2;15/11 13/4;17/9 13/6;19/7 14/3;17/11 14/5;19/9 15/2;17/13 15/4;19/11
16/3;19/13 17/2;19/15
らすかるさんからのコメントです。(平成25年11月4日付け)
a/s;b/t=2/1;3/1 3/1;4/2 3/2;5/1 4/1;5/3 4/2;6/2 4/3;7/1 5/1;6/4 5/2;7/3
5/3;8/2 5/4;9/1 6/1;7/5 6/2;8/4 6/3;9/3 6/4;10/2 6/5;11/1 7/1;8/6
7/2;9/5 7/3;10/4 7/4;11/3 7/5;12/2 7/6;13/1
のように綺麗に並ぶはずなのですが…。このうち 4/2;6/2 は 2/1;3/1 を単に縦横2倍
にしたものなので、除外する気持ちもわからなくもないですが...。
6/5;11/1 や 7/6;13/1 が抜けている理由は不明です。
らすかるさんからのコメントです。(平成25年11月3日付け)
一般に、a<b<2a を満たすa、bに対して、s=b-a、t=2a-b とすれば、元の問題と同じ形で
成り立ちます。
よおすけさんからのコメントです。(平成25年11月3日付け)
答えは「135°」で、GAIさん正解です。解答の方針は、数学感動秘話の「2つの角の和」の
問題と同じです。
S(H)さんからのコメントです。(平成25年11月3日付け)
よおすけさんからのコメントです。(平成25年11月4日付け)
弧度法もOKです。その場合は、∠AEB+∠AFD=3π/4となります。逆三角関数を使われて
解いているようなので、∠AEBと∠AFDはおよそ何度かを書きます。
∠AEB=arccos(5/13)≒ 67.38° ∠AFD=arccos(7/13√2)≒ 67.62°