・　２つの角の和　 　　 　 　　　　　　　　　　　　　Ｓ．Ｈ氏

　平成１９年９月１６日（日）の「熱血！平成教育学院」でマス北野から出題された図形の問
題は面白かった。

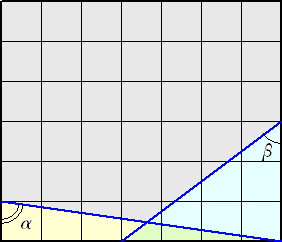
　下図の格子状の長方形において、角 α＋β の大きさを求めよ。

三角関数の加法定理を知っていれば、 　　　ｔａｎα＝７　、ｔａｎβ＝４/３　なので、 　　　ｔａｎ（α＋β） 　　　＝（ｔａｎα＋ｔａｎβ）/（１−ｔａｎαｔａｎβ） 　　　＝（７＋４/３）/（１−７・４/３） 　　　＝−１　　より、　α＋β＝１３５° 　　　と直ちに答は出るが味気ない。

　劇団ひとりさんは「山勘」で正解されたそうだが、その方が、ずっと味があるように思える。

　この問題は次のように解くのがエレガントらしい。これだと中学入試問題レベル位かな？

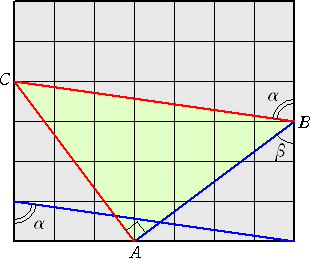左図において、△ＡＢＣは、 　　　　　∠Ａ＝∠Ｒ　、　ＡＢ＝ＡＣ 　　の直角２等辺三角形。 　　　よって、 　　　　α＋β＝１８０°−４５°＝１３５° 　　となる。

　解法がとても美しいですね。すぐ三角関数に頼ってしまう私は反省しなくては．．．。